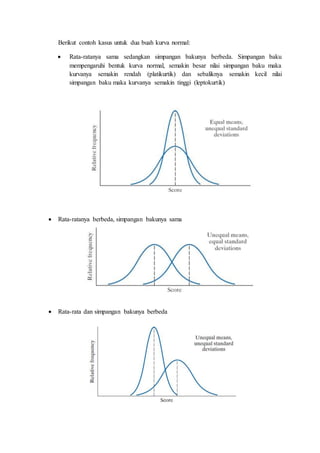
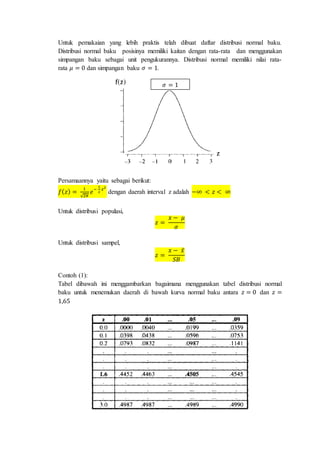
Dokumen ini membahas berbagai distribusi probabilitas, termasuk distribusi binomial, poisson, dan normal, serta aplikasi masing-masing dalam analisis data. Setiap distribusi dijelaskan dengan rumus, contoh soal, dan cara perhitungan yang memberikan pemahaman tentang penerapan dalam situasi nyata. Selain itu, terdapat tabel distribusi normal baku yang memfasilitasi penggunaan dalam penelitian dan praktik statistika.

1. Distibusi Binomial, Poisson, Distribusi Normal dan
Aplikasinya
Disusun Oleh : Kelompok 4
Nama : Aisyah Turidho (06081281520073)
: Reno Sutriono (06081381520044)
: M. Rizky Tama Putra (06081381419045)
Mata Kuliah : Statistika Dasar
Dosen : Prof. Dr. Ratu Ilma Indra Putri, M.Si
: Puji Astuti, S.Pd., M.Sc
Fakultas Keguruan dan Ilmu Pendidikan
Program Studi Matematika
Universitas Sriwijaya Palembang
2016

2. DAFTAR ISI
DAFTAR ISI...............................................................................................................................i
DISTIBUSI BINOMIAL, POISSON, DISTRIBUSI NORMAL DAN APLIKASINYA.........1
A. Distribusi Binomial..........................................................................................................1
B. Distribusi Poisson............................................................................................................ 2
C. Distribusi Normal............................................................................................................ 4
LAMPIRAN 1
LAMPIRAN 2
DAFTAR PUSTAKA

3. DISTIBUSI BINOMIAL, POISSON, DISTRIBUSI NORMAL DAN
APLIKASINYA
A. Distribusi Binomial
Dalam berbgai percobaan dimana variabel yang sedang diteliti adalah tingkat nominal
maka hanya ada 2 kemungkinan nilai atau hasil dari variabel tersebut. Misalnya
Salesmen pandai atau tidak pandai menjual barang dagangan, anak yang baru lahir
kedua lelaki atau perempuan, dan petani berhasil atau gagal panen padi di tahun ini.
Sampel yang melibatkan variabel yang dapat diwakili oleh probabilitas teoritis
distribusi disebut distribusi binomial, dikatakan binomial karena terdapat dua hasil
yang mungkin.
Jika pada tiap percobaan dalam eksperimen, 𝑃( 𝐴) = 𝜋 harganya tetap maka
percobaan yang berulang-ulang itu dinamakan percobaan Bernoulli. Jika dilakukan
percobaan tersebut sebanyak 𝑁 kali, 𝑋 diantaranya menghasilkan peristiwa A dan
sisanya ( 𝑁 − 𝑋) peristiwa 𝐴̅. 𝑃( 𝐴) = 𝜋 maka 1 − 𝜋 = 𝑃(𝐴̅), peluang terjadinya
peristiwa A sebanyak 𝑋 = 𝑥 kali diantara 𝑁 , dihitung dengan cara berikut:
𝑝( 𝑥) = 𝑃( 𝑋 = 𝑥) = (
𝑁
𝑛
) 𝜋 𝑥 (1 − 𝜋) 𝑁−𝑥
Dimana n = banyaknya kejadian yang dikehendakai dan x = kejadian yang diharapkan
Dengan 𝑥 = 0,1,2,3, … ., 𝑁 ; 0 < 𝜋 < 1 maka didapat cara mencari koefisien binom:
(
𝑁
𝑥
) =
𝑁!
𝑥! (𝑁 − 𝑥)!
Distribusi binomial mempunyai parameter, diantaranya ialah rata-rata 𝜇 dan
simpangan baku 𝜎, rumusnya yaitu:
𝜇 = 𝑁𝜋
𝜎 = √𝑁𝜋(1 − 𝜋)
Contoh Soal:
Misal dalam suatu rumah sakit terdapat 4 orang yang medonorkan darahnya, dalam
populasi tersebut ada 2 kemungkinan yaitu orang yang bertipe darah O dan bukan
darah O, dimana peluang orang bertipe darah O adalah 0,4 dan peluang yang bertipe
darah bukan O adalah 0,6. Tentukan peluang 3 orang yang bertipe darah O dari 4
orang itu?
Penyelesaian:
Hal pertama yang harus dilakukan yaitu dengan membuat kemungkinan tipe dara dari
4 pendonor itu, dilambangkan O yang bertipe darah O dan N yang bertipe darah
bukan O.

4. Banyak Yang
Bertipe Darah O
Hasil yang Mungkin
0 NNNN
1 ONNN, NONN, NNON, NNNO
2 OONN, ONON, ONNO, NOON, NONO, NNOO
3 NOOO, ONOO, OONO, OOON
4 OOOO
𝑝(3) = 𝑃( 𝑁𝑂𝑂𝑂 ∪ 𝑂𝑁𝑂𝑂 ∪ 𝑂𝑂𝑁𝑂 ∪ 𝑂𝑂𝑂𝑁)
𝑝(3) = 𝑃( 𝑁𝑂𝑂𝑂) + 𝑃( 𝑂𝑁𝑂𝑂) + 𝑃( 𝑂𝑂𝑁𝑂)+ 𝑃( 𝑂𝑂𝑂𝑁)
𝑝(3) = (0,6)(0,4)3
+ (0,4)(0,6)(0,4)2
+ (0,4)2(0,6)(0,4)+ (0,4)3(0,6)
𝑝(3) = 4 (0,4)3
(0,6)
𝑝(3) = 0,1536
Atau bisa juga diselesaikan dengan menggunakan rumus distribusi binomial:
𝑝( 𝑥) = 𝑃( 𝑋 = 𝑥) = (
𝑁
𝑛
) 𝜋 𝑥
(1 − 𝜋) 𝑁−𝑥
𝑝(3) = (
4
3
) (0,4)3
(0,6)
𝑝(3) = [
4!
3! (4 − 3)!
](0,4)3
(0,6)
𝑝(3) = 4 (0,4)3
(0,6)
B. Distribusi Poisson
Distribusi poisson adalah kemungkinan model yang tepat untuk jenis percobaan
tertentu. Variabel acak diskrit X dikatakan mempunyai distribusi poisson jika fungsi
peluangnya berbentuk:
𝑝( 𝑥) = 𝑃( 𝑋 = 𝑥) =
𝑒−𝜆 𝜆 𝑥
𝑥!
Dengan 𝑥 = 1,2,3, …, sedangkan 𝑒 = 𝑏𝑖𝑙𝑎𝑛𝑔𝑎𝑛 𝑘𝑜𝑛𝑠𝑡𝑎𝑛 = 2,7183 dan
𝜆 ( 𝑑𝑖𝑏𝑎𝑐𝑎 𝑙𝑎𝑚𝑑𝑎) = 𝑏𝑖𝑙𝑎𝑛𝑔𝑎𝑛 𝑡𝑒𝑡𝑎𝑝. Untuk harga 𝑒−𝜆
dapat dicari dengan
menggunakan kalkulator atau dengan melihat daftar harga 𝑒−𝜆
yang dapat anda lihat
dari berbagai sumber di internet. Distribusi poisson mempunyai parameter:
𝜇 = 𝝀
𝜎 = √𝜆
Distribusi poisson sering digunakan untuk menentukan peluang sebuah peristiwa yang
dalam area kesempatan tertentu diharapkan terjadinya sangat jarang. Contoh: dalam
tempo setiap 5 menit, operator telepon banyak menerima permintaan nomor untuk
disambungkan, diharapkan jarang sekali terjadi salah sambung.

5. Distribusi poisson dapat pula dianggap sebagai pendekatan kepada distribusi
binomial. Jika dalam distribusi binomial, N cukup besar sedangkan 𝜋 = peluang
terjadinya peristiwa A, sangat dekat kepada nol sedemikian 𝜆 = 𝑁𝑝 tetap maka
distribusi binomial didekati oleh distribusi poisson. Untuk penggunaannya, sering
dilakukan pendekatan ini jika 𝑁 ≥ 50 sedangkan 𝑁𝑝 < 5.
Contoh soal:
Dalam suatu Posyandu terdapat program suntik vaksin anti campak. Peluang
seseorang akan mendapat reaksi buruk setelah disuntik besarnya 0,0005. Dari 4000
orang yang disuntik, tentukan peluang yang mendapat reaksi buruk:
a. Tidak ada
b. Ada 2 orang
c. Lebih dari 2 orang
d. Tentukan ada berapa orang diharapkan yang akan mendapat reaksi buruk
Penyelesaian:
a. Dengan menggunakan pendekatan distribusi poisson kepada distribusi binomial,
maka 𝜆 = 𝑁𝑝 = 4000 × 0,0005 = 2. Jika X = banyak orang yang mendapat
reaksi buruk akibat suntikan itu, maka:
𝑝(0) =
𝑒−2
20
0!
= 0,1353
b. X = 2 sehingga:
𝑝(2) =
𝑒−2
22
2!
= 0,2706
c. X = 3, 4, 5, ...
Tetapi 𝑝(0) + 𝑝(1) + 𝑝(2)+ 𝑝(3) + ⋯ = 1 , maka
𝑝(3) + 𝑝(4) + ⋯ = 1 − 𝑝(0) − 𝑝(1)− 𝑝(2)
𝑝(1) =
𝑒−2
21
1!
= 0,2706
𝑝(3) + 𝑝(4) + ⋯ = 1 − 0,1353 − 0,2706 − 0,2706 = 0,3235
d. 𝜆 = 𝑁𝑝 = 4000 × 0,0005 = 2

6. C. Distribusi Normal
Distribusi yang paling penting dan banyak digunakan semua distribusi kontinu adalah
distribusi normal. Distribusi normal disebut juga distribusi gauss, distribusi normal
berasal dari distribusi dengan peubah acak kontinu. Persamaan distribusi gauss adalah
sebagai berikut:
𝑓( 𝑥) =
1
𝜎 √2𝜋
𝑒
−
1
2
(
𝑥− 𝜇
𝜎
)
2
dimana 𝜋 = 𝑘𝑜𝑛𝑠𝑡𝑎𝑛𝑡𝑎 𝑦𝑎𝑛𝑔 𝑛𝑖𝑙𝑎𝑖𝑛𝑦𝑎 𝑠𝑎𝑚𝑎 𝑑𝑒𝑛𝑔𝑎𝑛 3,1416
𝑒 = 𝑘𝑜𝑛𝑠𝑡𝑎𝑛𝑡𝑎 𝑦𝑎𝑛𝑔 𝑛𝑖𝑙𝑎𝑖𝑛𝑦𝑎 𝑠𝑎𝑚𝑎 𝑑𝑒𝑛𝑔𝑎𝑛 2,7183
𝜇 = 𝑝𝑎𝑟𝑎𝑚𝑒𝑡𝑒𝑟 𝑦𝑎𝑖𝑡𝑢 𝑛𝑖𝑙𝑎𝑖 𝑟𝑎𝑡𝑎 − 𝑟𝑎𝑡𝑎 𝑑𝑎𝑟𝑖 𝑑𝑖𝑠𝑡𝑟𝑖𝑏𝑢𝑠𝑖 𝑝𝑜𝑝𝑢𝑙𝑎𝑠𝑖
𝜎 = 𝑝𝑎𝑟𝑎𝑚𝑒𝑡𝑒𝑟 𝑦𝑎𝑛𝑔 𝑚𝑒𝑟𝑢𝑝𝑎𝑘𝑎𝑛 𝑠𝑖𝑚𝑝𝑎𝑛𝑔𝑎𝑛 𝑏𝑎𝑘𝑢 𝑑𝑖𝑠𝑡𝑟𝑖𝑏𝑢𝑠𝑖 𝑝𝑜𝑝𝑢𝑙𝑎𝑠𝑖
𝑥 = 𝑝𝑒𝑢𝑏𝑎ℎ 𝑘𝑜𝑛𝑡𝑖𝑛𝑢 𝑦𝑎𝑛𝑔 𝑑𝑎𝑒𝑟𝑎ℎ ( 𝑗𝑎𝑛𝑔𝑘𝑎𝑢𝑎𝑛) 𝑛𝑖𝑙𝑎𝑖𝑛𝑦𝑎 − ∞ < 𝑥 < ∞
Sifat distribusi normal:
a. Grafiknya selalu teletak diatas sumbu x selalu terletak diatas sumbu x
b. Bentuk grafiknya simetris terhadap 𝑥 = 𝜋
c. Mean, median dan modus sama untuk sebuah kurva normal yaitu tercapai pada
𝜇 =
0,3989
𝜎
d. Grafiknya asymtotis teradap sumbu x
e. Luas daerah grafik sama dengan satu satuan persegi

7. Berikut contoh kasus untuk dua buah kurva normal:
 Rata-ratanya sama sedangkan simpangan bakunya berbeda. Simpangan baku
mempengaruhi bentuk kurva normal, semakin besar nilai simpangan baku maka
kurvanya semakin rendah (platikurtik) dan sebaliknya semakin kecil nilai
simpangan baku maka kurvanya semakin tinggi (leptokurtik)
 Rata-ratanya berbeda, simpangan bakunya sama
 Rata-rata dan simpangan bakunya berbeda

8. Untuk pemakaian yang lebih praktis telah dibuat daftar distribusi normal baku.
Distribusi normal baku posisinya memiliki kaitan dengan rata-rata dan menggunakan
simpangan baku sebagai unit pengukurannya. Distribusi normal memiliki nilai rata-
rata 𝜇 = 0 dan simpangan baku 𝜎 = 1.
Persamaannya yaitu sebagai berikut:
𝑓( 𝑧) =
1
√2𝜋
𝑒
−
1
2
𝑧2
dengan daerah interval z adalah −∞ < 𝑧 < ∞
Untuk distribusi populasi,
𝑧 =
𝑥 − 𝜇
𝜎
Untuk distribusi sampel,
𝑧 =
𝑥 − 𝑥̅
𝑆𝐵
Contoh (1):
Tabel dibawah ini menggambarkan bagaimana menggunakan tabel distribusi normal
baku untuk menemukan daerah di bawah kurva normal baku antara 𝑧 = 0 dan 𝑧 =
1,65
𝜎 = 1

9. Kurva menunjukkan area yang sesuai sebagai berbayang wilayah di bawah kurva.
Nilai 1,65 dapat ditulis sebagai 1,6 + 0,05, dan dengan menempatkan 1,6 di bawah
kolom berlabel z dan kemudian bergerak ke kanan 1,6 sampai Anda datang di bawah
0,05 kolom Anda menemukan area 0,4505. Ini adalah daerah yang ditunjukkan pada
kurva dibawah ini. Misal daerah ini dinyatakan sebagai P (0 < 𝑧 < 1,65) = 0,4505.
Untuk daerah di bawah kurva normal baku antara 𝑧 = −1,65 dan 𝑧 =
0 direpresentasikan sebagai P(−1,65 < 𝑧 < 0) dan ditunjukkan pada kurna dibawah
ini. Oleh karena simetri maka P(−1,65 < 𝑧 < 0) = P(0 < 𝑧 < 1,65), kita tahu bahwa
P(0 < 𝑧 < 1,65) = 0,4505 dan oleh karena itu, P(1,65 < 𝑧 < 0) =0,4505.
Contoh (2):
Untuk daerah di bawah kurva normal normal antara 𝑧 = −1,65 dan 𝑧 = 1,65
diwakili oleh P(−1,65 < 𝑧 < 1,65) dan ditunjukkan pada kurva dibawah ini.
Probabilitas P(−1,65 < 𝑧 < 1,65) dinyatakan sebagai P(−1,65 < 𝑧 < 1,65) =
P(−1,65 < 𝑧 < 0) + P(0 < 𝑧 < 1,65). Dari contoh sebelumnya kita ketahui nilai
P(−1,65 < 𝑧 < 0) dan P(0 < 𝑧 < 1,65) dan jumlah kedua nilai P tersebut sama
dengan 0,9010. Oleh karena itu, P(−1,65 < 𝑧 < 1,65) = 0,9010.

10. Contoh (3):
Probabilitas dari peristiwa 𝑧 < 1,96 diwakili oleh P(𝑧 < 1,96) dan ditunjukkan pada
kurva dibawah ini.
Daerah yang ditunjukkan pada kurva diatas, dibagi menjadi 2 bagian seperti yang
ditunjukkan pada kurva dibawah ini, Daerah yang lebih gelap dari dua daerah itu
sama dengan P(𝑧 < 0) = 0,5 karena daerah itu merupakan setengah dari total luas
daerah. Daerah yang lebih terang dari dua daerah itu dinyatakan dalam P(0 < 𝑧 <
1,96) dan nilainya dapat dilihat pada daftar distribusi normal baku yang dapat anda
cari di internet atau sumber manapun, nilainya yaitu 0,4750. Jumlah dari dua daerah
tersebut adalah 0,5 + 0,4750 = 0,9750. Jadi, P(𝑧 < 1,96) = P(𝑧 < 0) + P(0 < 𝑧 <
1,96) = 0,5 + 0,4750 = 0,9750.
Perhatikan kurva dibawah ini, daerah dibawah z dapat dinyatakan 𝑧 > 1,96 dan
probabilitasnya dwakilkan P(𝑧 > 1,96). Untuk mengitung nilai P maka gunakan
konsep komplemen suatu kejadian. Komplemen dari P(𝑧 > 1,96) adalah P(𝑧 <
1,96). P(𝑧 > 1,96) + P(𝑧 < 1,96) = 1, dari contoh diatas dapat dilihat bahwa P(𝑧 <
1,96) = 0,9750. Jadi, P(𝑧 > 1,96) = 1 − P( 𝑧 < 1,96) = 1 − 0,9750 = 0,250

11. Contoh Soal:
15% dari tamatan SMA merupakan hasil PMDK. Sampel acak yang berukuran 600
tamatan SMA telah digunakan. Tentukan nilai kemungkinan yang akan terdapat:
a. Paling sedikit 70 orang dan paling banyak 80 sebagai basil PMDK.
b. Lebih besar atau sama dengan 100 orang yang memperoleh PMDK.
Penyelesaian:
a. x terletak antara : (70 − 0,5) < 𝑥 < (80 + 0,5) atau 69,5 < 𝑥 < 80,5
𝜇 = 0,15 × 600 = 90
𝜎 = √600 × 0,15 × 0,85 = 8,75
𝑧1 =
69,5−90
8,75
= −2,34 atau 𝑧2 =
80,5−90
8,75
= −1,09
Untuk luas daerah maka lihat tabel F yang dapat Anda cari dari berbagai sumber, baik
dari internet maupun buku. Luas daerah 𝑧−2,34 = 0,4904 dan luas daerah 𝑧−1,09 =
0,3621. Luas daerah antara 𝑧−2,34 dan 𝑧−1,09 = 0,4904 − 0,3621 = 0,1283. Maka
nilai kemungkinan terdapat paling sedikit 70 orang dan paling banyak 80 orang
sebagai hasil PMDK ada 0,1283.
b. Lebih besar atau sama dengan 100 artinya 𝑥 ≥ 99,5
1,09
0,1379
𝑧 ≥
99,5 − 90
8,75
= 1,09
Luas daerah 𝑧1,09 = 0,3621 maka banyak siswa
yang termasuk PMDK lebih besar atau sama
dengan 100 adalah 0,50 − 0,3621 = 0,1379

12. LAMPIRAN 1

13. LAMPIRAN 2

14. DAFTAR PUSTAKA
Coladarci, T.; Cobb, C. D.; Minium, E. W.; & Clarke, R. B. (2004). Fundamentals of
Statistical Reasoning in Education. Edisi 3. United State of America: Library of
Congress Cataloging-in-Publication Data. Hlm. 88 dan 90
Dowdy, S.; Weardon, S.; & Chilko, D. (2004). Statistics for Research. Edisi 3. Canada:
Wiley Interscience.Hlm. 49-50 dan 81
Herrhyanto, N., & Hamid, H. A. (2007). Statistika Dasar. Jakarta: Universitas Terbuka. Hlm.
7.3-7.4 dan 7.13
Sthepens, L. J. (1998). Schaums's Outline of Theory and Problems of Beginning Statistics.
United state of America: Library of Congress Cataloging-in-Publication Data.Hlm.
115-120
Sudjana. (2002). Metoda Statistika. Edisi 6. Bandung: Tarsito. Hlm. 130-136