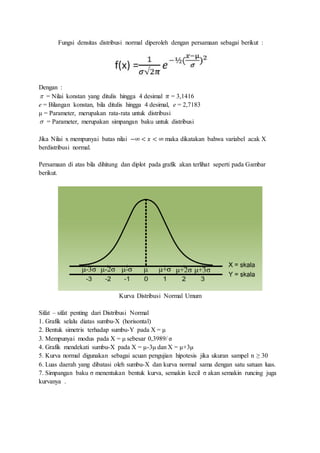
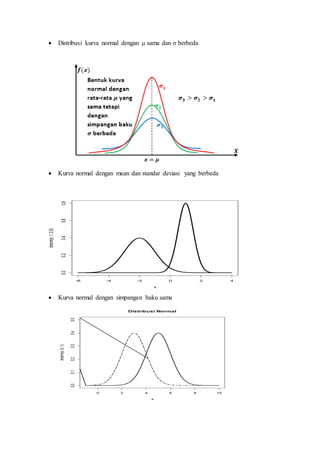
Dokumen ini membahas tentang distribusi binomial, poisson, dan normal, serta aplikasinya dalam statistika. Distribusi binomial merupakan hasil dari percobaan bernoulli yang memiliki dua hasil, sedangkan distribusi poisson digunakan untuk probabilitas kejadian langka dalam interval tertentu. Selain itu, distribusi normal yang dikenal dengan bentuk lonceng mencakup variabel acak kontinu dan memiliki sifat-sifat khusus.

1. 1. Distribusi Binomial
Sebelum mengetahui definisi dari distribusi binomial,kita terlebih dahulu harus
mengetahui percobaan binomial karena distribusi binomial merupakan hasil dari
percobaan binomial. Percobaan binomial ditemukan oleh seorang ahli matematika yang
berkebangsaan Swiss yaitu Jacob Bernoulli. Karena penemu percobaan binomial ini
ditemukan oleh Bernoulli maka percobaan ini bisa disebut percobaan Bernoulli. Percobaan
Bernoulli (Bernoulli Trial ) merupakan suatu performans dari suatu percobaan,percobaan ini
hanya memiliki dua macam keluaran yaitu “Sukses” atau “Gagal” (Sigit Nugroho : 2008).
Distribusi binomial memiliki ciri-ciri sebagai berikut :
1. Tiap percobaan (eksperimen) hanya memiliki 2 kategori hasil yaitu sukses (S) atau
gagal (G) yaitu dapat kita tuliskan dengan ruang sampel { S,G }.
2. Setiap eksperimen memiliki hasil eksperimen yang bersifat independent yaitu hasil
dari setiap percobaan tersebut tidak akan mempengaruhi percobaan lain.
3. Probabilitas (peluang ) percobaan tersebut dikategorikan sukses harus sama bagi
setiap percobaan.
4. Eksperimen terdiri atas banyaknya (n) yang merupakan bilangan tetap bagi setiap
percobaan
Dari uraian diatas,dapat disimpulkan bahwa Percobaan Binomial (Bernoulli )
adalah suatu percobaan atau eksperimen dimana setiap percobaan tersebut hanya
memiliki dua pilihan kemungkinan jawaban.
Hasil – hasil dari percobaan binomial dan peluang( probabilitas ) yang bersesuaian
dari hasil percobaan tersebut dinamakan Distribusi Binomial.Distribusi binomial adalah
salah satu jenis dari Distribusi Teoritis. Distribusi teoritis merupakan alat yang digunakan
untuk menentukan apa yang dapat diharapkan , apabila asumsi-asumsi yang dibuat benar
(Supranto, 2001: 32).
Dapat ditarik kesimpulan , Distribusi Binomial adalah suatu distribusi teoritis
yang berisi hasil dari sebuah percobaan(eksperimen) binomial dimana hasil tersebut
sudah sesuai dengan peluang (probabilitas) atau distribusi binomial juga bisa kita
sebut dengan sebutan peluang (probabilitas).
Notasi-notasi yang umumnya digunakan dalam percobaan binomial dan distribusi
binomial adalah sebagai berikut.
Notasi Keterangan
P(S) Simbol untuk peluang sukses
P(F) Simbol untuk peluang gagal
p Peluang sukses
q Peluang gagal
P(S) = p dan P(F) = 1 – p = q
n Banyaknya percobaan

2. x Banyaknya sukses dalam n kali
percobaan
Perhatikan bahwa 0 ≤ X ≤ n dan X = 0, 1, 2, 3, …, n.
Peluang(Probabilitas) Binomial yang sesuai dengan distribusi binomial dapat dihitung dengan
menggunakan rumus :
Contoh :
1. Koin terdiri dari satu angka dan satu gambar.Ketika kita melempar koin,kita akan
mendapatkan dua kemungkinan hasil yaitu gambar atau angka.Sekarang kita
mempunyai 3 koin, tentukan probabilitas dari 3 koin tersebut akan menghasilkan tepat
2 angka!
Jawab :
Soal diatas dapat diselesaikan dengan melihat ruang sampelnya. Ruang sampel dari
pelemparan satu koin sebanyak tiga kali adalah
S = {AAA, AAG, AGA, GAA, GGA, GAG, AGG, GGG}
Dari ruang sampel, kita dapat melihat bahwa ada tiga cara untuk mendapatkan tepat
dua angka, yaitu AAG, AGA, dan GAA. Sehingga peluang kita mendapatkan tepat
dua angka adalah 3/8 atau 0,375.
Contoh 1 dapat juga kita selesaikan dengan menggunakan keempat kriteria percobaan
binomial karena :
1. Terdapat tiga kali percobaan.
2. Setiap percobaan hanya memiliki dua kemungkinan, yaitu angka (A) atau gambar (G).
3. Hasil dari masing-masing percobaan saling bebas (hasil dari suatu pelemparan tidak
mempengaruhi hasil pelemparan lainnya).
4. Peluang percobaan sukses (angka) adalah ½ di setiap percobaannya.
Dalam kasus ini, n = 3, X = 2, p = ½, dan q = ½. Sehingga dengan mensubstitusi nilai-
nilai tersebut ke dalam rumus, kita mendapatkan
Jawaban tersebut sama dengan jawaban kita sebelumnya yang menggunakan ruang
sampel.

3. 1.1 Parameter Distribusi Binomial
Parameter distribusi binomial adalah sebagai berikut : rata-rata (𝜇) , varians ( 𝜎)2
dan
simpangan baku ( 𝜎).
1. Rata-rata
Perhatikan bahwa 𝑋 = ∑ 𝑌𝑖 = 𝑌1 + 𝑌2 + ⋯+ 𝑌𝑛
Dan 𝑌𝑖 akan bernilai 1 jika “sukses”  𝑝( 𝑠𝑢𝑘𝑠𝑒𝑠) = 𝑝(1) = 𝑝, bernilai 0 jika
“gagal”  𝑝( 𝑔𝑎𝑔𝑎𝑙) = 𝑝(0) = 1 − 𝑝 = 𝑞
Sehingga,
𝐸( 𝑌𝑖) = 1( 𝑝) + 0(1 − 𝑝) = 𝑝 + 0 = 𝑝, untuk semua 𝑖
𝐸( 𝑋) = 𝐸(∑ 𝑌𝑖) = 𝐸( 𝑌1) + 𝐸( 𝑌2) + ⋯+ 𝐸( 𝑌𝑛)
𝐸( 𝑋) = 𝐸(∑ 𝑌𝑖) = 𝑝 + 𝑝 + ⋯+ 𝑝 (𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 𝑛 𝑘𝑎𝑙𝑖)
𝐸( 𝑋) = 𝐸(∑ 𝑌𝑖) = 𝑛𝑝
Jadi, rata-rata dari distribusi binomial adalah 𝑛𝑝.
2. Varians
Turunan rumus diatas hampir sama dengan turunan rumus rata-rata sehingga
menghasilkan
3. Simpangan baku ( 𝜎)
Turunan rumus diatas hampir sama dengan turunan rumus rata-rata sehingga
menghasilkan :
𝜇 = 𝑛𝑝
𝜎2 = 𝑛. 𝑝. 𝑞
𝜎 = √ 𝑛𝑝𝑞

4. 2. Distribusi Poisson
Distribusi poisson ditemukan oleh seorang ahli matematika kelahiran Prancis yang
bernama S.D Poisson (1781-1841).Distribusi poisson adalah distribusi teoritis yang
digunakan untuk menentukan probabilitas suatu kejadian yang jarang terjadi dalam suatu
interval waktu tertentu atau di suatu daerah tertentu.
Adapun ciri-ciri distribusi poisson adalah sebagai berikut:
1. Percobaan di satu selang tertentu tak bergantung pada selang lain.
2. Peluang terjadinya satu percobaan singkat atau pada daerah yang kecil
(jarang terjadi)
3. Peluang lebih dari satu hasil percobaan alkan terjadi dalam selang waktu
yang singkat tersebut, dapat diabaikan.
Probabilitas sukses dari distribusi Poisson dapat diselesaikan dengan rumus:
Dengan :
x = 0,1,2,3,....,dst
e = bilangan euler = bilangan alam = bilangan natural = 2,71828
𝜆 = rata – rata terjadinya suatu peristiwa ( n x p )
2.1 Parameter Distribusi Poisson
1. Rata-rata (𝝁)
2. Simpangan Baku (𝝈)
3. Distribusi Normal
Distribusi normal adalah distribusi dari variabel acak kontinu. Kadang-kadang
distribusi normal disebut juga dengan distribusi Gauss. Distribusi ini merupakan distribusi
yang paling penting dan paling banyak digunakan di bidang statistika. Distribusi ini
menyerupai bentuk lonceng (Bell Shape) dengan nilai rata-rata X sebagai sumbu simetrisnya.
𝑝𝑟( 𝑥) =
𝜆 𝑥 𝑒−𝑥
𝑥!
𝜇 = 𝜆
𝜎 = √𝜆

5. Fungsi densitas distribusi normal diperoleh dengan persamaan sebagai berikut :
Dengan :
 = Nilai konstan yang ditulis hingga 4 desimal 𝜋 = 3,1416
e = Bilangan konstan, bila ditulis hingga 4 desimal, e = 2,7183
μ = Parameter, merupakan rata-rata untuk distribusi
 = Parameter, merupakan simpangan baku untuk distribusi
Jika Nilai x mempunyai batas nilai −∞ < 𝑥 < ∞ maka dikatakan bahwa variabel acak X
berdistribusi normal.
Persamaan di atas bila dihitung dan diplot pada grafik akan terlihat seperti pada Gambar
berikut.
Kurva Distribusi Normal Umum
Sifat – sifat penting dari Distribusi Normal
1. Grafik selalu diatas sumbu-X (horisontal)
2. Bentuk simetris terhadap sumbu-Y pada X = μ
3. Mempunyai modus pada X = μ sebesar 0,3989/ σ
4. Grafik mendekati sumbu-X pada X = μ-3μ dan X = μ+3μ
5. Kurva normal digunakan sebagai acuan pengujian hipotesis jika ukuran sampel n ≥ 30
6. Luas daerah yang dibatasi oleh sumbu-X dan kurva normal sama dengan satu satuan luas.
7. Simpangan baku σ menentukan bentuk kurva, semakin kecil σ akan semakin runcing juga
kurvanya .

6.  Distribusi kurva normal dengan  sama dan  berbeda
 Kurva normal dengan mean dan standar deviasi yang berbeda
 Kurva normal dengan simpangan baku sama
0 2 4 6 8 10
0.00.10.20.30.40.5
x
dnorm(x,5,1)
Distribusi Normal
-6 -4 -2 0 2 4
0.00.20.40.60.8
x
dnorm(x,1,0.5)

7. Untuk menyelesaikan persoalan dalam menyelesaikan integral fungsi kepadatan peluangnya ,
maka dapat diatasi dengan mentransformasikan variabel acak normal X menjadi variabel
acak Z .
Dimana z =
𝑥− 𝜇
𝜎
Sehingga X~N ( μ , σ2) sama artinya dengan Z~N (0 , 1)
Z~N (0 , 1) dibaca Z terdistribusi normal dengan rata-rata 0 dan varians 1
dengan μ = 0 dan 𝜎= 1 sehingga fungsi densitasnya berbentuk :
Dengan batas z −∞ < 𝑧 < ∞
Perubahan grafiknya dapat dilihat pada gambar dibawah ini :
Setelah distribusi normal baku yang didapat dari distribusi normal umum maka
daftar distribusi normal baku dapat digunakan. Bagian-bagian luas distribusi
normal baku dapat dicari. Caranya adalah :
1. Hitung z sehingga dua desimal
2. Gambarkan kurvanya seperti gambar normal standar
3. Letakkan harga z pada sumbu datar, lalu tarik garis vertikal hingga
memotong kurva.
6. Dari z di kolom kiri maju ke kanan dan dari z di baris atas turun ke bawah, maka
didapat bilangan yang merupakan luas yang dicari. Bilangan yang didapat harus
dituliskan dalam bentuk 0,xxxx (bentuk 4 desimal).
4. Luas yang tertera dalam daftar adalah luas daerah antara garis ini dengan

8. garis tegak di titik nol.
5. Dalam tabel normal cari tempat harga z pada kolom paling kiri hanya satu
desimal dan desimal keduanya dicari pada baris paling atas.
Penggunaan Tabel Distribusi Normal
Untuk keperluan praktis, para ahli statistika telah menyusun Tabel distribusi normal baku dan
tabel tersebut dapat ditemukan hampir di semua buku teks Statistika. Tabel distribusi normal
baku disebut juga dengan Tabel Z dan dapat digunakan untuk mencari peluang di bawah
kurva normal secara umum, asal saja nilai µ dan σ diketahui. Sebagai catatan nilai µ dan σ
dapat diganti masing-masing dengan nilai x dan S. Berikut tabel distribusi normal baku :

9. Misalnya dari hasil perhitungan diperoleh nilai Z = 1,96
 Maka di kolom kiri kita cari nilai1,9 dan baris atas kita cari angka 6
 Dari kolom 6 bergarak ke bawah, hingga pertemuan titik yang menunjukkan angka
0,4750.
 Berarti luas daerah di dalam kurva normal antara rata-rata dengan 1,96 SD ke kanan
adalah 0,475.
 Karena luas kurva ke kanan dan ke kiri sama, maka luas penyimpangan 1,96 ke kanan
dan ke kiri dari rata-rata adalah 0,95 (95%).
Fenomena distribusi data normal :
• Kira-kira 68,27% dari kasus ada dalam daerah satu simpangan baku sekitar rata-rata, yaitu
antara μ - σ dan μ + σ.
• Ada 95,45% dari kasus terletak dalam daerah dua simpangan baku sekitar rata-rata, yaitu
antara μ - 2σ dan μ + 2σ.

10. • Hampir 99,73% dari kasus ada dalam daerah tiga simpangan baku sekitar rata – rata, yaitu
antara μ - 3σ dan μ + 3σ
4. Aplikasi Distribusi Binomial,Distribusi Poisson dan Distribusi Normal
4.1 Aplikasi Distribusi Binomial
Contoh Soal :
Sebuah mata uang logam dilemparkan sebanyak 8 kali.Berapa probabilitas binomial muncul
gambar sebanyak 5 kali? Berapa nilai rata-rata ? Varians ? Simpangan Baku?
Jawab :
Diketahui : n = 8
X = 5
p = ½
q= 1-p = 1 – ½ = ½
Ditanya : a. probabilitas binomial = ...?
b. nilai rata-rata =...?
c. Varians=...?
d. Simpangan Baku=...?
Penyelesaian : 𝑎. 𝑃 ( 𝑋 = 5) =
𝑛!
(𝑛−𝑋)!𝑋!
× 𝑝 𝑥
× 𝑞 𝑛−𝑥
=
8!
3!5!
× (
1
2
)
5
× (
1
2
)
3
=
8 ×7 ×6 ×5×4×3×2×1
(3×2×1)(5×4×3×2×1)
×
1
32
×
1
8
=
8 ×7×6
3×2×1
×
1
32
×
1
8
= 56 ×
1
32
×
1
8
=
7
32
b. 𝜇 = 𝑛. 𝑝
= 8 (
1
2
)

11. = 4
c. 𝜎2
= 𝑛. 𝑝. 𝑞
= 5 (
1
2
)(
1
2
)
=
5
4
= 1.25
d. 𝜎 = √ 𝑛𝑝𝑞
= √
5
4
= 1.1
4.2 Aplikasi Distribusi Poisson
Contoh Soal :
Dua ratus siswatelahmendaftaruntuk ikutolimpiadeMatematika.JikaProbabilitassiswayangtelah
mendaftartidakdatangadalah0,01 maka berapakahpeluangada3 orang siswayangtidak
mengikuti olimpiade Matematikatersebut?
Jawab:
𝑛 = 200
𝑝 = 0,01
𝑥 = 3
𝑒 = 2,71828
𝜇 = 𝑛𝑝 = 200 .0,01 = 2
!
.
);(
x
e
P
x
x


 

!3
71828,2.2 23 

= 0,1804

12. 2. Rata – rata seorang sekretaris baru melakukan lima kesalahan mengetik per
halaman. Berapakah peluang bahwa pada halaman berikut ia :
1. Tidak ada kesalahan ( x = 0 )
2. Tidak lebih dari tiga kesalahan ( x ≤ 3) atau ( 0,1,2,3 )
3. Lebih dari tiga kesalahan ( x > 3 ) atau ( 4,…,15)
Jawab :
. Dik : μ = 5
a. x = 0
!
.
);(
x
e
P
x
x


 

!0
71828,2.5 50
)5;0(

P
= 0.0067
b. x ≤ 3 ;
!
.
);(
x
e
P
x
x


 

P (x ≤ 3 , 5) = P( x 1, μ ) +….+p(x3, μ)
= P( 0, 5 ) + P (1, 5 ) + P ( 2, 5 ) + P ( 3, 5 )
= 0.0067 + 0.0337 + 0.0842 + 0.1404
= 0.2650
c. X > 3 ini berarti
X= 4,5, 6,....
Tetapi P(0;5) + P(1;5) + P(2;5) + P(3;5) = 1 maka
P (X > 3 , 5) = 1 – [P(0;5) + P(1;5) + P(2;5) + P(3;5)]

13. P (X > 3 , 5) = 1 – [P(0;5) + P(1;5) + P(2;5) + P(3;5)]
= 1 – [ 0.2650 ]
= 0,735
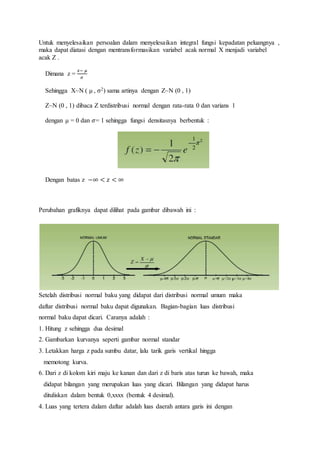
4.3 Aplikasi Distribusi Normal
Contoh Soal :
1. Jika Z~N 0 , 1 , maka tentu kan P ( Z ≤ 0,23 )
Jawab :
Z~N(0,1) dibaca Z terdistribusi normal dengan μ=0 dan σ2=1
Yang ditanya adalah peluang Z kurang dari 0,23 atau P(Z≤0,23)
Gunakan tabel distribusi normal, di bawah z pada kolom kiri cari 0,2 dan diatas sekali cari
angka 3. Dari 0,2 maju ke kanan dan 3 menurun, didapat 0,5910. Luas daerah = daerah
diarsir = 0,5910
2. Rata-rata produktivitas padi di Aceh tahun 2009 adalah 6 ton per ha, dengan simpangan
baku (s) 0,9 ton. Jika luas sawah di Aceh 100.000 ha dan produktivitas padi berdistribusi
normal (data tentatif), tentukan
a. berapa luas sawah yang produktivitasnya lebih dari 8 ton ?

14. b. berapa luas sawah yang produktivitasnya kurang dari 5 ton ?
Jawab :
Jawaban Soal a
1. Hitung nilai z dari nilai x = 8 ton dengan rumus
𝑍 =
𝑥 − x
𝑠
=
8 − 6
0,9
=
2
0,9
= 2,22
2. Hitung luas di bawah kurva normal pada z = 2,22.
Caranya buka Tabel Z dan lihat sel pada perpotongan baris 2,20 dan kolom 0,02. Hasilnya
adalah angka 0,98679 dan bila dijadikan persen menjadi 98,679%. Angka ini menunjukkan
bahwa luas di bawah kurva normal baku dari titik 2,22 ke kiri kurva adalah sebesar 98,679%.
Karena luas seluruh di bawah kurva normal adalah 100%, maka luas dari titik 2,22 ke kanan
kurva adalah 100% – 98,679% = 1,321% (arsir warna hitam pada gambar). Oleh karena itu,
luas sawah yang produktivitasnya lebih dari 8 ton adalah 1,321%, yaitu (1,321/100) x
100.000 ha = 1321 ha.
Jawaban soal b
1. Hitung nilai z dari nilai x = 5 ton, dengan rumus
𝑍 =
𝑥 − x
𝑠
=
5 − 6
0,9
=
−1
0,9
= −1,11
2. Hitung luas di bawah kurva normal pada z = -1,11.
Caranya buka Tabel Z dan lihat sel pada perpotongan baris -1,10 dan kolom 0,01. Hasilnya
adalah angka 0,13350 dan bila dijadikan persen menjadi 13,35%. Angka ini menunjukkan
bahwa luas di bawah kurva normal baku dari titik -1,11 ke kiri kurva adalah sebesar 13,35%
(diarsir warna hitam pada gambar). Oleh karena itu, luas sawah yang produktivitasnya
kurang dari 5 ton adalah 13,35%, yaitu (13,35/100) x 100.000 ha = 13350 ha.