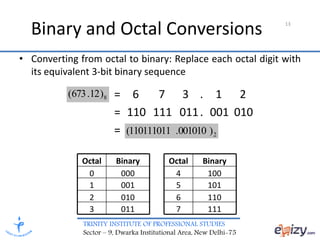
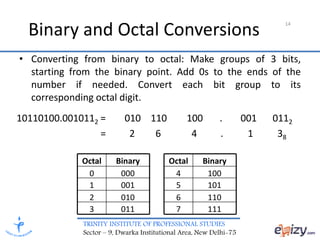
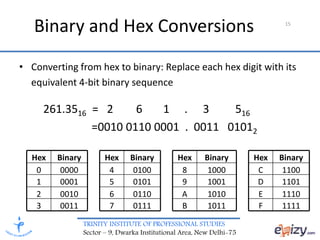
The document discusses number systems, focusing on positional notation and various bases including decimal, binary, octal, and hexadecimal. It explains how to convert between these systems and details specific methods for decimal to binary and binary to decimal conversions, as well as conversions between binary and octal or hexadecimal. Overall, it provides foundational knowledge on how numbers operate within different bases.

1. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
Affiliated Institution of G.G.S.IP.U, Delhi
DIGITAL ELECTRONICS
Paper Code :- BCA 106
Keywords:
Number System, Binary, Decimal, Octal, Hexa
By :-HARI MOHAN JAIN

2. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
2
Number System

3. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
3
Positional Notation
•Value of number is determined by multiplying each
digit by a weight and then summing.
•The weight of each digit is a POWER of the RADIX
(also called BASE) and is determined by position.
2
2
1
1
0
0
1
1
2
2
3
3
210123 .







rararararara
aaaaaa

4. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
4
Radix (Base) of a Number System
• Decimal Number System (Radix = 10)
Eg:- 7392 = 7x103+3x102+9x101+2x100
• Binary Number System (Radix = 2)
Eg:- 101.101 = 1x22+0x11+1x20+1x2-1+0x2-11x2-2
• Octal number system (radix = 8)
• Hexadecimal number system (radix = 16)

5. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
5
Radix (Base) of a Number System
• When counting upwards in base-10, we increase the
units digit until we get to 10 when we reset the units
to zero and increase the tens digit.
• So, in base-n, we increase the units until we get to n
when we reset the units to zero and increase the n-s
digit.
• Consider hours-minutes-seconds as an example of a
base-60 number system:
– Eg. 12:58:43 + 00:03:20 = 13:02:03
NB. The base of a number is often indicated by a subscript.
E.g. (123)10 indicates the base-10 number 123.

6. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
6
Decimal Number Systems
• Base 10
– Ten digits, 0-9
– Columns represent (from right to left) units, tens,
hundreds etc.
123
1102 + 2101 + 3100
or
1 hundred, 2 tens and 3 units

7. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
7
Binary Number System
• Base 2
– Two digits, 0 & 1
– Columns represent (from right to left) units, twos,
fours, eights etc.
1111011
126 + 125 + 124 + 123 + 022 + 121 + 120
= 164 + 132 + 116 + 18 + 04 + 12 + 11
= 123

8. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
8
Decimal to Binary Conversion
123  2 = 61 remainder 1
61  2 = 30 remainder 1
30  2 = 15 remainder 0
15  2 = 7 remainder 1
7  2 = 3 remainder 1
3  2 = 1 remainder 1
1  2 = 0 remainder 1
Least significant bit (LSB)
(rightmost)
Most significant bit (MSB)
(leftmost)
Answer : (123)10 = (1111011)2
Example – Converting (123)10 into binary

9. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
9
Decimal to Binary Conversion
The quotient is divided by 2
until the new quotient
becomes 0
Integer Remainder
41
20 1
10 0
5 0
2 1
1 0
0 1 101001 answer

10. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
10
Converting Decimal to Binary
• To convert a fraction, keep multiplying the fractional part by 2 until it becomes
0. Collect the integer parts in forward order
• Example: 162.375:
• So, (162.375)10 = (10100010.011)2
162 / 2= 81 rem 0
81 / 2 = 40 rem 1
40 / 2 = 20 rem 0
20 / 2 = 10 rem 0
10 / 2 = 5 rem 0
5 / 2 = 2 rem 1
2 / 2 = 1 rem 0
1 / 2 = 0 rem 1
0.375 x 2 = 0.750
0.750 x 2 = 1.500
0.500 x 2 = 1.000

11. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
11
Binary to Decimal Conversion
• Each bit represents a power of 2
• Every binary number is a sum of powers of 2
• Decimal Value = (dn-1  2n-1) + ... + (d1  21) + (d0  20)
• Binary (10011101)2 = 27 + 24 + 23 + 22 + 1 = 157
1 0 0 1 1 1 0 1
27 26 25 24 23 22 21 20
01234567
Some common
powers of 2

12. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
12
Converting Binary to Decimal
• For example, here is 1101.01 in binary:
1 1 0 1 . 0 1 Bits
23
22
21
20
2-1
2-2
Weights (in base 10)
(1 x 23) + (1 x 22) + (0 x 21) + (1 x 20) + (0 x 2-1) + (1 x 2-2) =
8 + 4 + 0 + 1 + 0 + 0.25 = 13.25
(1101.01)2 = (13.25)10

13. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
13
Binary and Octal Conversions
• Converting from octal to binary: Replace each octal digit with
its equivalent 3-bit binary sequence
= 6 7 3 . 1 2
= 110 111 011. 001 010
=
11170113
11060102
10150011
10040000
BinaryOctalBinaryOctal
8)12.673(
2)001010.110111011(

14. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
14
Binary and Octal Conversions
• Converting from binary to octal: Make groups of 3 bits,
starting from the binary point. Add 0s to the ends of the
number if needed. Convert each bit group to its
corresponding octal digit.
10110100.0010112 = 010 110 100 . 001 0112
= 2 6 4 . 1 38
11170113
11060102
10150011
10040000
BinaryOctalBinaryOctal

15. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
15
Binary and Hex Conversions
• Converting from hex to binary: Replace each hex digit with its
equivalent 4-bit binary sequence
261.3516 = 2 6 1 . 3 516
=0010 0110 0001 . 0011 01012
1111F1011B0111700113
1110E1010A0110600102
1101D100190101500011
1100C100080100400000
BinaryHexBinaryHexBinaryHexBinaryHex

16. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
16
Binary and Hex Conversions
• Converting from binary to hex: Make groups of 4 bits, starting
from the binary point. Add 0s to the ends of the number if
needed. Convert each bit group to its corresponding hex digit
10110100.0010112 = 1011 0100 . 0010 11002
= B 4 . 2 C16
1111F1011B0111700113
1110E1010A0110600102
1101D100190101500011
1100C100080100400000
BinaryHexBinaryHexBinaryHexBinaryHex