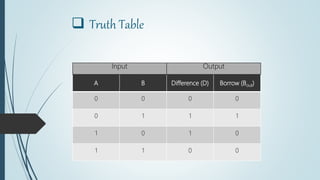
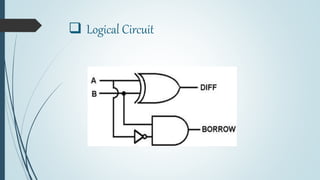
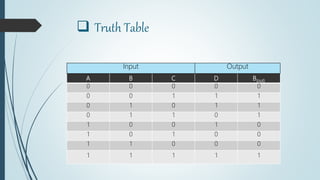
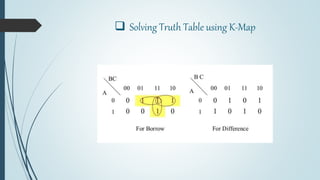
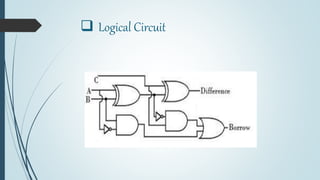
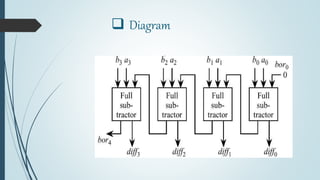
This document discusses digital subtractors. It defines a subtractor as an electronic logic circuit that calculates the difference between two binary numbers. There are two main types: half subtractors and full subtractors. A half subtractor is used for single bit subtraction and has two inputs, two outputs, and a truth table. A full subtractor can subtract three single bit numbers, with three inputs and two outputs defined by its truth table. Parallel binary subtractors are built by cascading multiple full subtractors to subtract larger binary numbers. Subtractors have applications in signal processing, arithmetic logic units, address calculation, and more.

1. DIGITAL ELECTRONICS
SUBTRACTOR

2.  Group Members:
1. Md Jahid Hasan – 152-15-5588
2. Allahma Iqbal – 152-15-6094
3. MD. Shahnur Chowdhury – 153-15-6387
4. Umme Sharmin Ritu – 161-15-6883

3.  Objectives
 Definition of Subtractor
 Types of subtractor
 Explaining different subtractors with
 Truth table
 Boolean Expression
 Logic circuit
 Parallel binary subtractor
 Applications

4.  What is Subtractor ?
Subtractor is an electronic logic circuit
for calculating the difference between
two binary numbers which provides the
difference and borrow as output.

5.  Types of Subtractor
 Half Subtractor
 Full Subtractor

6.  Half subtractor
Half Subtractor is used for subtracting
one single bit binary number from another
single bit binary number.
It has two inputs; Minuend (A) and
Subtrahend (B) and two outputs; Difference
(D) and Borrow (Bout).

7.  Truth Table
A B Difference (D) Borrow (Bout)
0 0 0 0
0 1 1 1
1 0 1 0
1 1 0 0
Input Output

8.  Solving truth table using K-map
Borrow = Ā.B Difference = A ⊕ B

9.  Boolean Expression
From the truth table and K-map, the Boolean
Expression can be derived as:
Difference (D) = Ā.B + A. 𝐁 = A ⊕ B
Borrow (Bout)= Ā.B

10.  Logical Circuit

11.  fULL subtractor
A logic Circuit Which is used for subtracting
three single bit binary numbers is known as
Full Subtractor.
It has three inputs; Minuend (A), Subtrahend
(B) and following Subtrahend (C) and two
outputs; Difference (D) and Borrow (Bout).

12.  Truth Table
A B C D B(out)
0 0 0 0 0
0 0 1 1 1
0 1 0 1 1
0 1 1 0 1
1 0 0 1 0
1 0 1 0 0
1 1 0 0 0
1 1 1 1 1
Input Output

13.  Solving Truth Table using K-Map

14.  K-Map Minimization
From the Truth Table The Difference and Borrow will
written as,
Difference=A'B'C+A'BC'+AB'C'+ABC
Reducing it we got,
Difference=A ⊕B ⊕C
Borrow=A'B'C+A'BC'+A'BC+ABC
=A'B'C+A'BC'+A'BC+A'BC+A'BC+ABC
=A'C(B'+B)+A'B(C'+C)+BC(A'+A)
Borrow=A'C+A'B+BC

15.  Boolean Expression
From the truth table and k-map minimization,
the Boolean Expression can be derived as:
D = A ⊕ B ⊕ C
B(out) = BC + (B ⊕ C) A

16.  Logical Circuit

17.  Parallel Binary Subtractor
Parallel binary subtractor can be implemented by
cascading several full-subtractors.
Next slide shows the block level representation of a
4-bit parallel binary subtractor, which subtracts 4-
bit b3b2b1b0 from 4-bit a3a2a1a0. It has 4-bit
difference output D3D2D1D0 with borrow output
B(out).

18.  Diagram

19.  Applications
 To attenuate the radio/audio signal
 In amplifier to reduce sound distortion
 In arithmetic logic unit of processors
 Increment and decrement operators
 Calculate addresses

20. Any question ?

21. THANK YOU