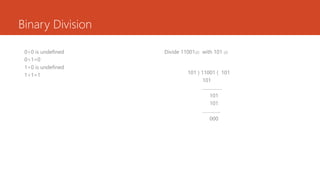
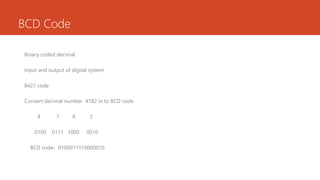
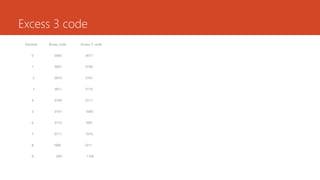
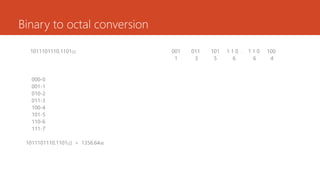
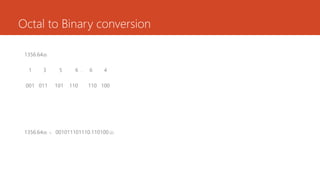
This document discusses digital electronics topics including number systems, codes, Boolean algebra, and digital circuits. It provides examples and explanations of converting between decimal, binary, octal, and hexadecimal number systems. Binary coded decimal, gray code, and excess-3 code are also defined. Combinational and sequential digital circuits as well as memory devices are listed as topics to be covered.

1. DIGITAL ELECTRONICS
K SATYNARAYANA RAJU
Department of physics and electronics
B V RAJU COLLEGE

2. TOPICS
Number systems and codes
Boolean algebra and theorems
Combinational digital circuits
Sequential digital circuits
Memory devices

3. Number systems and codes
Number systems
Decimal Number system
Binary Number system
Octal Number system
Hexa Decimal Number system
Codes
BCD Code
Gray Code
Excess-3 Code

4. Decimal Number system
Base or radix of a number system
Decimal number system- Base 10
Numerals or symbols- 0,1,2,3,4,5,6,7,8,9
Value- 1976.539(10) - 1×10^3+9×10^2+7×10^1+6×10^0+5×10^-1+3×10^-
2+9×10^-3

5. Binary Number systems
Binary number system- Base 2
Numerals or Symbols used- 0,1
Value- 11001.101= 1×2^4+1×2^3+0×2^2+0×2^1+1×2^0+1×2^-
1+0×2^-2+1×2^-3

6. Octal Number system
Octal Number system- Base 8
Numerals or Symbols used- 0,1,2,3,4,5,6,7,
Value- 26345.167= 2×8^4+6×8^3+3×8^2+4×8^1+5×8^0+1×8^-1+6×8^-2+7×8^-3

7. Hexa Decimal Number system
Hexa decimal Number system- Base 16
Numerals or Symbols used- 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
Value- B98.C6= 11×16^2+9×16^1+8×16^0+12×16^-1+6×16^-2

8. Decimal to Binary conversion
253.15(10) is a decimal number
Real part- 253
Fractional part- 15
For real part – Successive division by 2
Fractional part – Successive multiplication by 2
Real part- 253÷2=126-->1
126÷2=63 -->0
63÷2=31 -->1
31÷2=15 -->1
15÷2=7 --->1
7÷2=3 -->1
3÷2=1 --->1
1÷2=0 --->1
Collect the reminders from bottom to top
253.15(10) = 11111101.0010 (2)
Fractional part
0.15×2=0.30--->0
0.30×2=0.60--->0
0.60×2=1.20--->1
0.20×2=0.40--->0
Collect the quotients from top to bottom

9. Decimal to Octal conversion
7546.32(10) is a decimal number
Real part- 754
Fractional part- 32
For real part – Successive division by 8
Fractional part – Successive multiplication by 8
Real part- 7546÷8=943 -->2
943 ÷8=117 -->7
117÷ 8= 14 -->5
14÷8= 1 --> 6
1÷8=0 ---> 1
Collect the reminders from bottom to top
7546.32(10) = 16572.2436 (8)
Fractional part
0.32×8= 2.56---> 2
0.56×8= 4.48 --->4
0.48×8= 3.84--->3
0.84×8= 6.72--->6
Collect the quotients from top to bottom

10. Decimal to Hexadecimal conversion
6876.94(10) is a decimal number
Real part- 6876
Fractional part- 0.94
For real part – Successive division by 16
Fractional part – Successive multiplication by 16
Real part- 6876÷16=429-->12 (C)
429÷16=26 -->13(D)
26÷16=1 -->10 (A)
1÷16=0 -->1
Collect the reminders from bottom to top
6876.94(10) = 1ADC.F0A3 (16)
Fractional part
0.94×16= 15.04---> 15(F)
0.04×16= 0.64---> 0
0.64×16= 10.24 --> 10(A)
0.24× 16= 3.84 --->3
Collect the quotients from top to bottom

11. Binary to Decimal Conversion
11111101.0010 (2) is a binary number
Positional weights
1 1 1 1 1 1 0 1 . 0 0 1 0
2^7 2^6 2^5 2^4 2^3 2^2 2^1 2^0 2^-1 2^-2 2^-3 2^-4
1×2^7+1×2^6+1×2^5+1×2^4+1×2^3+1×2^2+1×2^1+0×2^0+0×2^-1+0×2^-2+1×2^-3+0× 2^-4
128+64+32+16+8+4+1+0.125= 253.125(10)
11111101.0010 (2) = 253.125(10)

12. Octal to Decimal Conversion
16572.2436(8)
1 6 5 7 2 . 2 4 3 6
8^4 8^3 8^2 8^1 8^0 8^-1 8^-2 8^-3 8^-4
1×8^4+ 6×8^3+5×8^2+7×8^1+2×2^0+2×8^-1+4×8^-2+3×8^-3+6×8^-4
4096+6×512+5×64+7×8+2×1+2×0.125+4×0.01562+3×0.001953+6×0.0002441
4096+3072+320+56+2+0.25+0.06248+0.005859+0.001464
16572.2436(8) = 7546.3198(10)

13. Hexa Decimal to Decimal conversion
1ADC.F0A3 (16)
1 A D C . F 0 A 3
16^3 16^2 16^1 16^0 16^-1 16^-2 16^-3 16^-4
1×16^3+10×16^2+13×16^1+12×16^0+15×16^-1+0×16^-2+10×16^-3+3×16^-4
= 4096+10×256+13×16+12+15×0.0625+10×0.00024414+3×0.000015258
= 4096+2560+208+12+0.9375+0.0024414+0.00004577
= 6876.9399
1ADC.F0A3 (16) = 6876.9399 (10)

14. Binary to octal conversion
1011101110.1101(2)
000-0
001-1
010-2
011-3
100-4
101-5
110-6
111-7
1011101110.1101(2) = 1356.64(8)
001 011 101 1 1 0 . 1 1 0 100
1 3 5 6 6 4

15. Octal to Binary conversion
1356.64(8)
1 3 5 6 . 6 4
001 011 101 110 110 100
1356.64(8) = 001011101110.110100 (2)

16. Binary to Hexadecimal conversion
110110101110101.1100100110(2)
0000-0
0001-1
0010-2
0011-3
0100-4
0101-5
0110-6
0111-7
1000-8
1001-9
1010-A
1011-B
1100-C
1101-D
1110-E
1111-F
110110101110101.1100100110 (2)= 6D75.C98 (16)
0110 1101 0111 0101. 1100 1001 1000
6 D 7 5 C 9 8

17. Hexa Decimal to Binary conversion
6D75.C98 (16)
6 D 7 5 . C 9 8
0110 1101 0111 0101 1100 1001 1000
6D75.C98 (16) = 0110110101110101.110010011000(2)

18. Octal to Hexa Decimal conversion
653.24(8)
6 5 3 . 2 4
110 101 011 010 100
110101011.010100
0001 1010 1011 . 0101 0000
1 A B 5 0
653.24(8) = 1AB.50 (16)

19. Hexa Decimal to octal conversion
A57. 2C(16)
A 5 7 . 2 C
1010 0101 0111 0010 1100
101001010111.00101100
101 001 010 111 . 001 011 000
5 1 2 7 1 3 0
A57. 2C(16) = 5127.130(2)

20. Binary Addition
• 0+0=00
• 0+1=01
• 1+0=01
• 1+1=10
• 1+1+1=11
• 1+1+1+1=100
• 1+1+1+1+1=101
Add 1011101.0101 to 1101001.1100
1 0 1 1 1 0 1 . 0 1 0 1
1 1 0 1 0 0 1 . 1 1 0 0
………………………………………………………………………………………………
1 1 0 0 0 1 1 1 0 0 0 1

21. Binary subtraction
• 0-0=0
• 1-0=1
• 1-1=0
• 0-1=1 with borrow 1
Perform 11001(2) - 10111(2)
1 1 0 0 1
1 0 1 1 1
………………………………………………………
0 0 0 1 0

22. 1’s complement method of subtraction
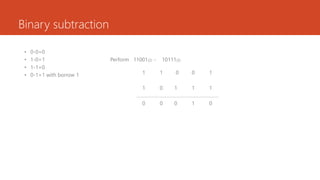
Perform 11001(2) - 10111(2) using 1’s complement method of subtraction
Minuend - 11001
Subtrahend- 10111
1’s complement of subtrahend - 01000
Add minuend with 1’s complement of subtrahend
11001
01000
……………..
[1]00001
Add carry 1 to 00001 to get the final result
00010

23. 2’s complement method of subtraction
Perform 11001(2) - 10111(2) using 2’s complement
method of subtraction
Minund - 11001
Subtrahend- 10111
1’s complement of subtrahend - 01000
2’s complement of subtrahend- 01000+1 = 01001
Add minuend with 1’s complement of subtrahend
11001
01001
• ……………..
• [1]00010
Leave the carry to get the final result
00010
Note:- if carry is 0 then find 2’s complement to
Result obtained after addition to get the final result.
•
•
•
• ```

24. Binary multiplication
0×0=0
0×1=0
1×0=0
1×1=1
Multiply 10110(2) with 110 (2)
1 0 1 1 0
× 1 1 0
……………………….
0 0 0 0 0
1 0 1 1 0
1 0 1 1 0
…… ..……………………………
1 0 0 0 0 1 0 0

25. Binary Division
0÷0 is undefined
0÷1=0
1÷0 is undefined
1÷1=1
Divide 11001(2) with 101 (2)
101 ) 11001 ( 101
101
.................
101
101
…………..
000

26. BCD Code
Binary coded decimal
Input and output of digital system
8421 code
Convert decimal number 4782 in to BCD code
4 7 8 2
0100 0111 1000 0010
BCD code- 0100011110000010

27. Gray code
Cyclic code or reflection code or unit distance code
Binary code Gray code
0000 0000
0001 0001
0010 0011
0011 0010
0100 0110
0101 0111
0110 0101
0111 0100
1000 1100
1001 1101

28. Excess 3 code
Decimal Binary code Excess 3 code
0 0000 0011
1 0001 0100
2 0010 0101
3 0011 0110
4 0100 0111
5 0101 1000
6 0110 1001
7 0111 1010
8 1000 1011
9 1001 1100