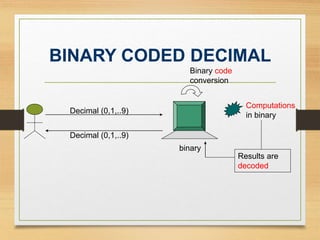
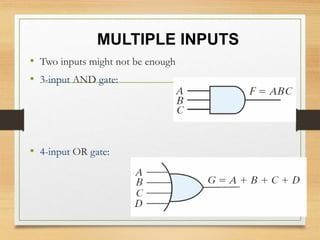
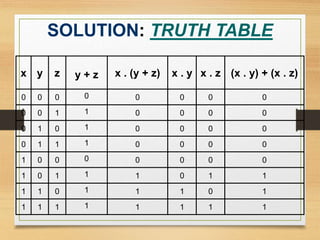
This document provides an overview of binary codes and Boolean algebra concepts. It discusses various binary codes like BCD, excess-3, and Gray codes. It also covers logical operations in Boolean algebra like AND, OR, and NOT. Properties of Boolean algebra like duality, De Morgan's laws, and absorption laws are explained. Digital logic gates are introduced as implementations of Boolean functions.

1. LECTURE - 4
Ms. Maria Saleemi

2. BINARY CODES
• BCD CODE
• BCD ADDITION
• EXCESS – 3 CODE
• 2421 CODE
• 842’1’ CODE
• GRAY CODE
• ASCII CODE

3. CODES
• Information given to computer
• Data
• Instructions
• Code must be in Binary
• Computer understand Binary (0 and 1)

4. CODES
• n-bit Binary Code
• Combination of bits (0’s and 1’s) = 2n
• Each Combination represents a different value

5. BINARY CODED DECIMAL
Decimal (0,1,..9)
binary
Binary code
conversion
Computations
in binary
Results are
decoded
Decimal (0,1,..9)

6. BCD
• 4-bit Code
• Each decimal digit (0,1,..9) is written as a 4-bit binary
number

7. CONVERSION
DECIMAL BCD
0 0 0 0 0
1 0 0 0 1
2 0 0 1 0
3 0 0 1 1
4 0 1 0 0
5 0 1 0 1
6 0 1 1 0
7 0 1 1 1
8 1 0 0 0
9 1 0 0 1

8. REPRESENTATION IN BCD
FOR VALUES > 9
(11)10 = (?)BCD
From Table write:
BCD value of 1 (space) BCD value of 1
(11)10 = (0001 0001)BCD

9. • BCD is not same as Binary No.s
(16)10 = (0001 0110)BCD = (10000)2

10. LIMITATIONS OF BCD
• BCD uses 4 places for each decimal digit

11. ADVANTAGES OF BCD
• Can be easily converted to Decimal
• Can be understood by Computers

12. EXERCISE
Convert :
• (146)10 = (?)BCD
• (1001 0111 0110)BCD = (?)10
• (1010 1001 1000)BCD = (?)10

13. BCD ADDITION
• How computer will perform Addition of two
numbers using BCD Code ??
Decimal BCD Decimal BCD
4 0100 4 0100
+ 5 + 0101 + 8 1000
9 = 1001 12 1100
Invalid BCD No.

14. ADDITION WHEN SUM > 9
• If sum becomes Greater than 9:
• ADD 6 (0110) to the Binary Sum
• WHY add 6 ??
• We have 4-bits for BCD.
• n = 4
• Possible Combinations are: 2n = 24 = 16
• Used Combinations = 10 (0,1,..9)
• Unused Combinations = 16 – 10 = 6

15. EXAMPLESDecimal BCD
8 1000
+9 +1001
17 10001
+ 0110
= 10111
Thus,
(17)10 = (0001 0111)BCD

16. EXAMPLES
(184 + 576)10 = (?)BCD
• Solve Units, Tens, Hundreds place separately
• Transfer Carry’s to the previous bits
• If sum exceeds 1001, ADD 6 (0110) to it

17. OTHER DECIMAL CODES (4-bit)
• BCD – 23222120 – 8421
• 2421
• EXCESS – 3
• 842’1’

18. 2421 CODE
• Till decimal value 4 write the code
• Decimal value 5 is the 1’s Complement of Decimal
Value 4
• 6 is the complement of 3
• 7 is the complement of 2
• 8 is the complement of 1
• 9 is the complement of 0

19. EXCESS – 3 CODE
• Add 3 (0011)BCD to every decimal value
• Example:
Decimal BCD Excess-3
0 0000 (0000 + 0011) = 0011
1 0001 (0001 + 0011) = 0100
… … …

20. 842’1’ CODE
• Against each decimal value
• Add 8 and 4
• Subtract 2 and 1 to make the appropriate code

21. PROPERTIES
• BCD , 2421, and 842’1’ are WEIGHTED Codes
• BCD has weights = 8421
• 2421 has weights = 2421
• 842’1’ has weights = 8 4 -2 -1

22. Lecture 6

23. GRAY CODE
• Like simple Binary Numbers
• Difference:
• Only 1 bit changes at a time
• ADVANTAGE
• Error Detection and Error Correction
• USES
• Rotating Shaft of an aero plane

24. ROTATING SHAFT OF AN
AERO PLANE
0º
90º
180º
270º
0
0
1
1
1
..

25. CONVERSIONS
• Binary to Gray Code
• Gray Code to Binary

26. BINARY TO GRAY CODE• First bit of Gray is same as First bit of Binary
• Compare the MSB of Binary with its next bit.
• If bits compared are same, write gray bit 0
• If bits compared are different, write gray bit1
• Number of bits should be Equal
(1 0 1 1 0 1)2 = (?)Gray
(1 1 1 0 1 1)Gray

27. ERROR DETECTION
• Detection of Errors during transmission
• Binary information is sent through WIRES
• Noise in the Wires can change 0 to 1 and 1 to
0
• A PARITY-BIT is added for error-detection

28. GRAY TO BINARY CODE• Start with MSB
• Binary bits are same as Gray bits up to and including first
1
• If Gray bit is 0, repeat the previous binary bit
• If Gray bit is 1, complement the previous binary bit
(0 0 1 1 1 0 1 1 )Gray = (?)2
(0 0 1 0 1 1 0 1)2

29. PARITY BIT
• An extra bit added to the information
• Added to make the total no. of 1’s in the coded group,
either ODD or EVEN
• Even Parity
• choose parity bit such that # of 1’s is even
• Odd Parity
• choose parity bit such that # of 1’s is odd

30. EXAMPLE
• Data=1000001, even parity=0, odd parity=1
• Data=1010100, even parity=1, odd parity=0
• Only one parity bit is used

31. ALPHANUMERIC CODES
• Upper Case Alphabets (A,B,..,Z)
• Lower Case Alphabets (a,b,..,z)
• Numeric Values (0,1,2…)
• Special Characters (@,$,*,%,#,^,…etc)

32. TYPES OF ALPHANUMERIC
CODES• ASCII (American Standard Code for Information
Interchange)
• 7-bit code
• EBCDIC (Extended BCD Interchange Code)
• 8-bit code

33. Lecture 7

34. BINARY LOGIC
• Describes the Processing of Binary Information
• Is also called Boolean Algebra
• Uses 2 possible values:
• ‘1’ and ‘0’
• ‘yes’ and ‘no’
• ‘true’ and ‘false’
• Can be represented by variables: A, B, C, x, y, z, …

35. LOGICAL OPERATIONS
3 basic logical operations
• AND
• OR
• NOT
• Others can be derived from those (NAND, XOR, etc.)

36. AND Function• Operation:
• Two inputs
• Output = 1 if and only if both inputs are 1
• Symbolized by dot or absence of operator
x·y or xy
• Truth table
• Needs to consider 22 = 4 input combinations
• Graphic symbol
• AND gate
111
001
010
000
zyx
inputs output

37. OR Function
• Two inputs
• Output = 1 if any one or both inputs are 1
• Symbolized by “plus” sign: x + y
• Truth table
• Graphic symbol
• OR gate
x y z
0 0 0
0 1 1
1 0 1
1 1 1

38. NOT Function
• Complement operation
• Single input
• Inverts value of input
• Symbolized by prime x’ or over bar
• Truth table
• Input combinations on the left
• Output of function on the right
• Graphic symbol
• NOT gate
• Little circle indicates inversion
x x'
0 1
1 0
x
input output

39. MULTIPLE INPUTS
• Two inputs might not be enough
• 3-input AND gate:
• 4-input OR gate:

40. ALGEBRAS
• What is an algebra?
• Mathematical system consisting of
• Set of elements
• Set of operators
• Axioms or postulates
• Why is it important?
• Defines rules of “calculations”
• Example: arithmetic on natural numbers
• Set of elements: N = {1,2,3,4,…}
• Operator: +, –, *
• Axioms: associativity, distributivity, closure, identity elements, etc.
• Note: operators with two inputs are called binary
• Does not mean they are restricted to binary numbers!

41. CHAPTER – 2
BOOLEAN ALGEBRA AND
LOGIC GATES

42. GEORGE BOOLE
• Father of Boolean algebra
George Boole (1815 - 1864)

43. TOPICS
• Boolean algebra
• Algebra axioms, postulates
• Boolean functions
• Algebraic expression
• Boolean Theorems
• Comparison of Boolean functions
• Canonical and standard forms
• sum of minterms
• Duality: DeMorgan’s theorem
• Dual canonical form (product of maxterms)
• Digital logic gates and integrated circuits

44. BOOLEAN ALGEBRA• Axioms and Postulates
1. Value of Variables
Variable x may have two values:
 x = 0 or x = 1
2. IDENTITY
(+) OR: 0 + x = x + 0 = x
(.) AND: 1 . x = x . 1 = x
******* ALSO *******
1 + x = 1
0 . x = 0

45. BOOLEAN ALGEBRA3. Commutative Law
OR (+):x + y = y + x
AND(.): x . y = y + x
3. Distributive Law
OR/AND: x + (y . z) = (x + y) . (x + z)
AND/OR: x . (y + z) = (x . y) + (x . z)
3. Complement
OR: x + x’ = 1
AND: x . x’ = 0
• Redundance Law
OR/AND: x + (x’ . y) = x + y (using distributive law)

46. BOOLEAN ALGEBRA –
DE-MORGAN’S THEOREM1. x + y + z + … = x . y . z . …
2. x . y . z . … = x + y + z + …
ABSORPTION LAW
1. x + x . y = x
2. x . (x + y) = x
**** ALSO ****
x + x = x
x . x = x

47. VERIFICATION USING TRUTH
TABLES
• Using Truth Table, Verify Distributive Law:
 x . (y + z ) = ( x . y ) + ( x . z )
We have 3 variables:
x , y, z
Possible Combinations: 23 = 8

48. SOLUTION: TRUTH TABLE
x y z y + z x . (y + z) x . y x . z (x . y) + (x . z)
0 0 0 0 0 0 0 0
0 0 1 1 0 0 0 0
0 1 0 1 0 0 0 0
0 1 1 1 0 0 0 0
1 0 0 0 0 0 0 0
1 0 1 1 1 0 1 1
1 1 0 1 1 1 0 1
1 1 1 1 1 1 1 1

49. EXERCISE
Prove:
• De-Morgan’s Law
• Commutative Law

50. BOOLEAN FUNCTIONS
• EXPRESSIONS that contain:
• Binary Variable
• Values = 0,1
• Binary Operators
• OR, AND, NOT
• Parenthesis
• Equal Sign

51. BOOLEAN FUNCTIONS -
REPRESENTATION• Truth Table
• Boolean Expression

52. TRUTH TABLE
Listing of all possible combinations of INPUTS
and
their resulting OUTPUTS

53. BOOLEAN EXPRESSION
• Represented as:
Output = Logic Operators ( Inputs )