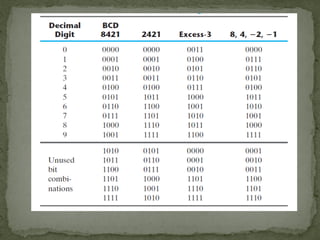
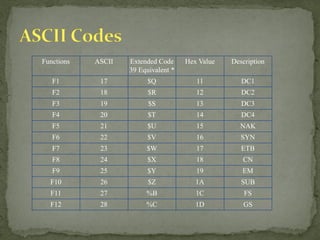
This document discusses various coding schemes including: - Binary coded decimal (BCD) which assigns a weight to each digit position to represent decimal numbers. Other positively weighted codes and negatively weighted codes are also discussed. - Gray code which minimizes the number of bit changes between adjacent values represented. This is useful for applications like thumbwheels. - Character encoding standards like ASCII, EBCDIC, and Unicode which can represent larger character sets with more bits per character. - Floating point number representation with sign, exponent and mantissa fields.

1. Dr. (Mrs.) Gargi Khanna
Associate Professor
Electronics & Communication Engg. Deptt..
National Institute of Technology Hamirpur
(HP)
By:-

2. o Codes
o Weighted and unweighted codes
o BCD, Excess-3, 2421, 84-2-1
o Gray Code
o Alphanumeric Code, Unicode

3.  Code:A set of n-bit strings in which different bit strings
represent different numbers or other things.
 Code word: a particular combination of n-bit values
N-bit strings =2N valid code words.
 To represent 10 decimal digits, at least need 4 bits.
 Excessive ways to choose ten 4-bit words. Some
common codes:
 BCD: Binary-coded decimal, also known as 8421 code
 2421,5421, Excess-3, Gray,
 Codes can be used to represent:
Numericals, Nonnumerical texts, Symbols
Events/Actions/States/Conditions

4. In weighted code, each digit position has a weight
or value. The sum of all digits multiplied by a
weight gives the total amount being represented.
We can express any decimal number in tens,
hundreds, thousands and so on.
Eg:- (4327)10= 4(10³)+3(10²)+2(10¹)+7(100)
BCD or 8421 is a type of weighted code where each
digit position is being assigned a specific weight.

5.  Positively weighted codes: All the weights asigned
to binary bits are positive
 17 positively weighted codes
 The first weight must be 1, second weight must be 1 or
2 and the sum of all weights must be equal and greater
than 9
 Eg 8421, 2421, 5211, 3321, 4311.
 Negatively weighted codes: some of the weights
assigned to binary bits are negative
 Eg 642-3, 84-2-1,74-2-1, 631-1

6.  In non-weighted code, there is no positional weight i.e.
each position within the binary number is not assigned
a prefixed value. No specific weights are assigned to bit
position in non –weighted code.
 The non-weighted codes are:-
 a) The Gray code b) The Excess-3 code

7.  Four bits are used to represent each decimal digit
 In each 4-bit group, 6 values are not used
 Many possible codes, natural BCD 8421 (equivalent
binary digits) most common
 BCD is not as efficient as binary
 BCD is easy to convert to/from decimal (it really is
decimal with different symbols)
 BCD add/subtract circuits are complex

8. Decimal
digit
BCD
8421 2421 5421 8 4 -2 -1 6 4 2 -3
Excess-
3
0 0000 0000 0000 0000 0000 0011
1 0001 0001 0001 0111 0101 0100
2 0010 0010 0010 0110 0010 0101
3 0011 0011 0011 0101 1001 0110
4 0100 0100 0100 0100 0100 0111
5 0101 1011 1000 1011 1011 1000
6 0110 1100 1001 1010 1000 1001
7 0111 1101 1010 1001 1101 1010
8 1000 1110 1011 1000 1010 1011
9 1001 1111 1100 1111 1111 1100
Positively Weighted codes Unweighted code
Negatively Weighted codes

9. Convert following to BCD form
a) 567310 b) 34210 c) 21810
Convert following BCD to their decimal equivalent
a) 10000110 b) 00110010.10010100
Convert the following binary numbers to
their BCD equivalent.
a) 1101.012 b) 11.0112
(Binary to decimal, then decimal to BCD)

10.  The codes representing the pair of complementary digits
are also complementary to each other.
 Example: Excess-3 code 0: 0011
1: 0100
2: 0101
3: 0110
4: 0111
5: 1000
6: 1001
7: 1010
8: 1011
9: 1100
241: 0101 0111 0100
758: 1010 1000 1011

12.  Gray codes are minimum change codes
 From one numeric representation to the next,
only one bit changes
 Primary use is in numeric input encoding apps.
where we expect non-random input values
changes (I.e. value n to either n-1 or n+1)
 Rotary shaft position

13. Binary to gray conversion:-
a)The MSB in the Gray code is same as the
corresponding bit in the binary number.
b)Going from left to right, add each adjacent pair of
binary bit to get next gray code bit and discard
carry

14. Gray to binary conversion:-
a)TheMSB is the binary code is
same as corresponding digit in the gray code.
b)Add each binary digit generated to the gray digit
in the next adjacent position and discard carry.

15. Binary
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
Gray
0000
0001
0011
0010
0110
0111
0101
0100
1100
1101
1111
1110
1010
1011
1001
1000

16. Gray Code
0 = 0000
1 = 0001
2 = 0011
3 = 0010
4 = 0110
5 = 1110
6 = 1010
7 = 1011
8 = 1001
9 = 1000
A Gray code changes by only 1 bit for
adjacent values. This is also called a
‘thumbwheel’ code because a
thumbwheel for choosing a decimal
digit can only change to an adjacent
value with each click of the
thumbwheel. This allows the binary
output of the thumbwheel to only
change one bit at a time; this can help
reduce circuit complexity, reduce signal
noise and result in less switching
events. Less switching results in
reduction in power dissipation

17.  Binary codes used to represent alphabetic and numeric
characters, symbols, control function
 Most common are:
 ASCII, 7 bit code, 128 symbols
 EBCDIC, 8 bit code, 256 symbols
 Unicode, 16 bit code
 Problems can arise when comparing symbol values
(collation)
 Comparing ‘A’ to ‘a’ in ASCII system yields different
results in an EBCDIC system.

18.  ASCII table
CS2100Number Systems and Codes 18
MSBs
LSBs 000 001 010 011 100 101 110 111
0000 NUL DLE SP 0 @ P ` p
0001 SOH DC1 ! 1 A Q a q
0010 STX DC2 “ 2 B R b r
0011 ETX DC3 # 3 C S c s
0100 EOT DC4 $ 4 D T d t
0101 ENQ NAK % 5 E U e u
0110 ACK SYN & 6 F V f v
0111 BEL ETB ‘ 7 G W g w
1000 BS CAN ( 8 H X h x
1001 HT EM ) 9 I Y i y
1010 LF SUB * : J Z j z
1011 VT ESC + ; K [ k {
1100 FF FS , < L l |
1101 CR GS - = M ] m }
1110 O RS . > N ^ n ~
1111 SI US / ? O _ o DEL
A: 1000001

19. Functions ASCII Extended Code
39 Equivalent *
Hex Value Description
F1 17 $Q 11 DC1
F2 18 $R 12 DC2
F3 19 $S 13 DC3
F4 20 $T 14 DC4
F5 21 $U 15 NAK
F6 22 $V 16 SYN
F7 23 $W 17 ETB
F8 24 $X 18 CN
F9 25 $Y 19 EM
F10 26 $Z 1A SUB
F11 27 %B 1C FS
F12 28 %C 1D GS

20. UNICODE is a 16-bit code for representing
alphanumeric data. With 16 bits, can represent 65536
different symbols.
16 bits = 2 Bytes per character.
$0041-005A A-Z
$0061-4007A a-z
Some other alphabet/symbol ranges
$3400-3d2d Korean Hangul Symbols
$3040-318F Hiranga, Katakana, Bopomofo, Hangul
$4E00-9FFF Han (Chinese, Japenese, Korean)
UNICODE used by Web browsers, Java, most software
these days.

21.  Due to the limitation of 7-bit ASCII code, American
National Standard Institute (ANSI) also extend the 7-
bit ASCII code to 8-bit code, known as Latin-I.
 Latin-I is an ISO standard.
 However, the 8-bit code still not adequate for
representing all possible characters in use Unicode.
 Unicode can represent 65,536 characters, of which
approximately 49,000 have been defined.
 More recent standard, Unicode 3.1 supports millions of
different characters.
 Unicode is multilingual in the most global sense.

22.  The usual floating point number
format consist of:
 A sign bit.
 An exponent
 A mantissa.

23.  Different input devices are used for converting original
data into computer format.
 Keyboard: Generate binary number code for each key.
 Microphone: Convert analog sound into binary data
using ADC.
 Camera: Convert analog picture into binary data using
ADC.
 Etc.

24.  Many different standards in use for different types of data. Some
common data representation are:
Type of data Standard
Alphanumeric ASCII, EBCDIC, Unicode
Image (bitmap) GIF(graphical image format), TIFF (tagged
image file format), PNG (portable network
graphics)
Image (object) PostScript, JPEG, SWF (Macromedia Flash),
SVG.
Outline graphics and
fonts
PostScript, TrueType
Sound WAV, AVI, MP3, MIDI, WMA
Page description Pdf (Adobe Portable Document Format),
HTML, XML.
Video Quicktime, MPEG-2, WMV