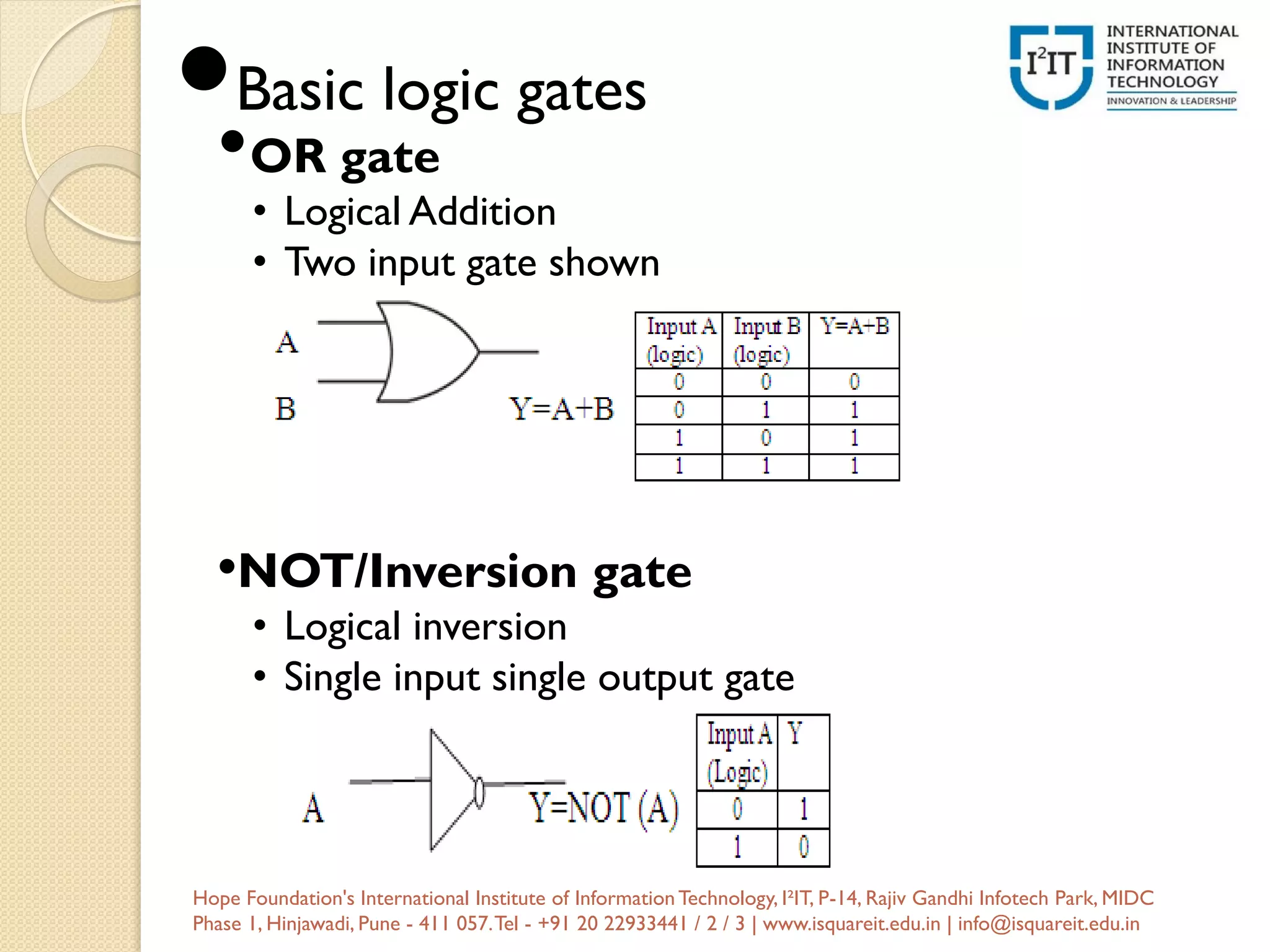
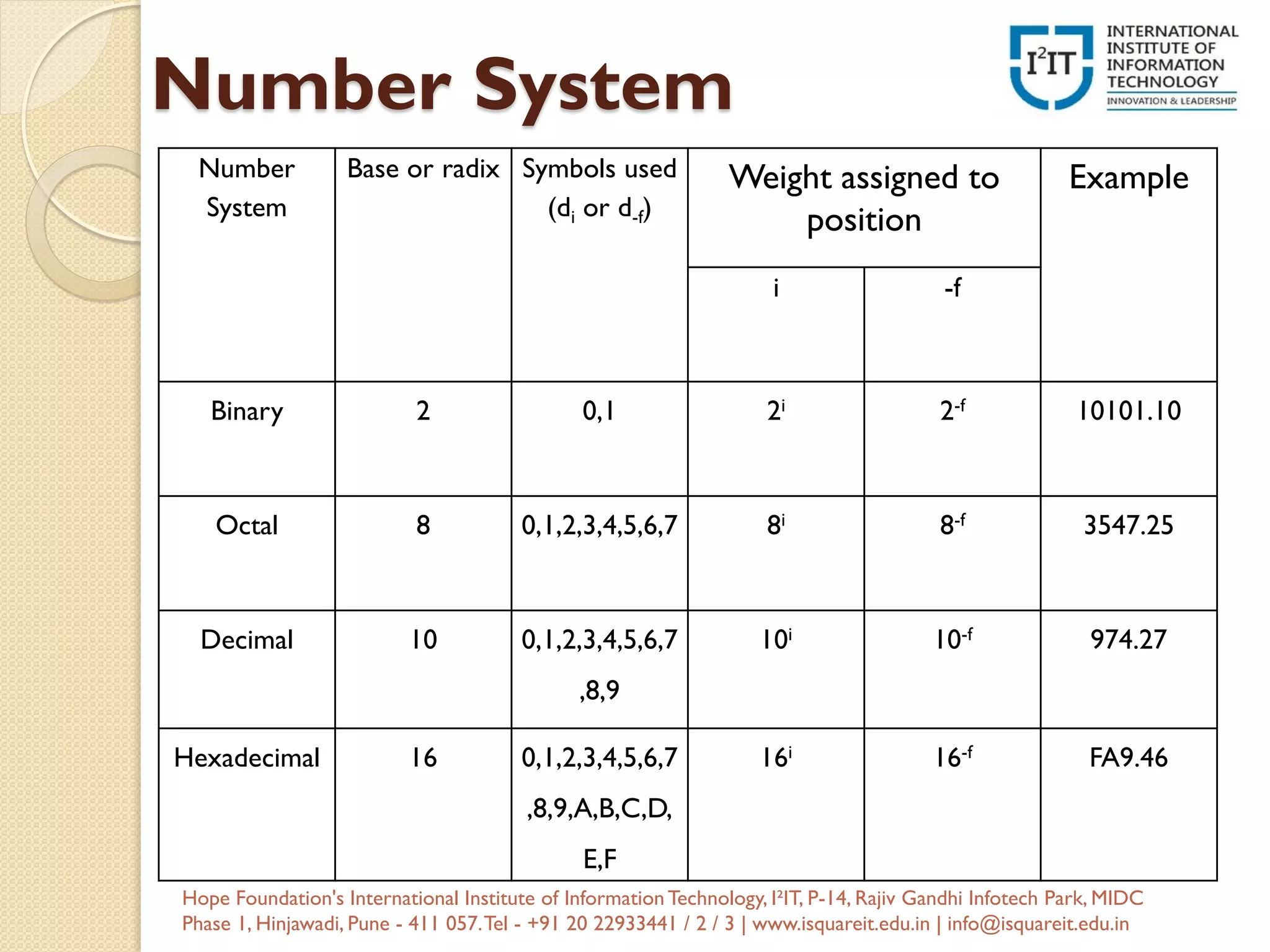
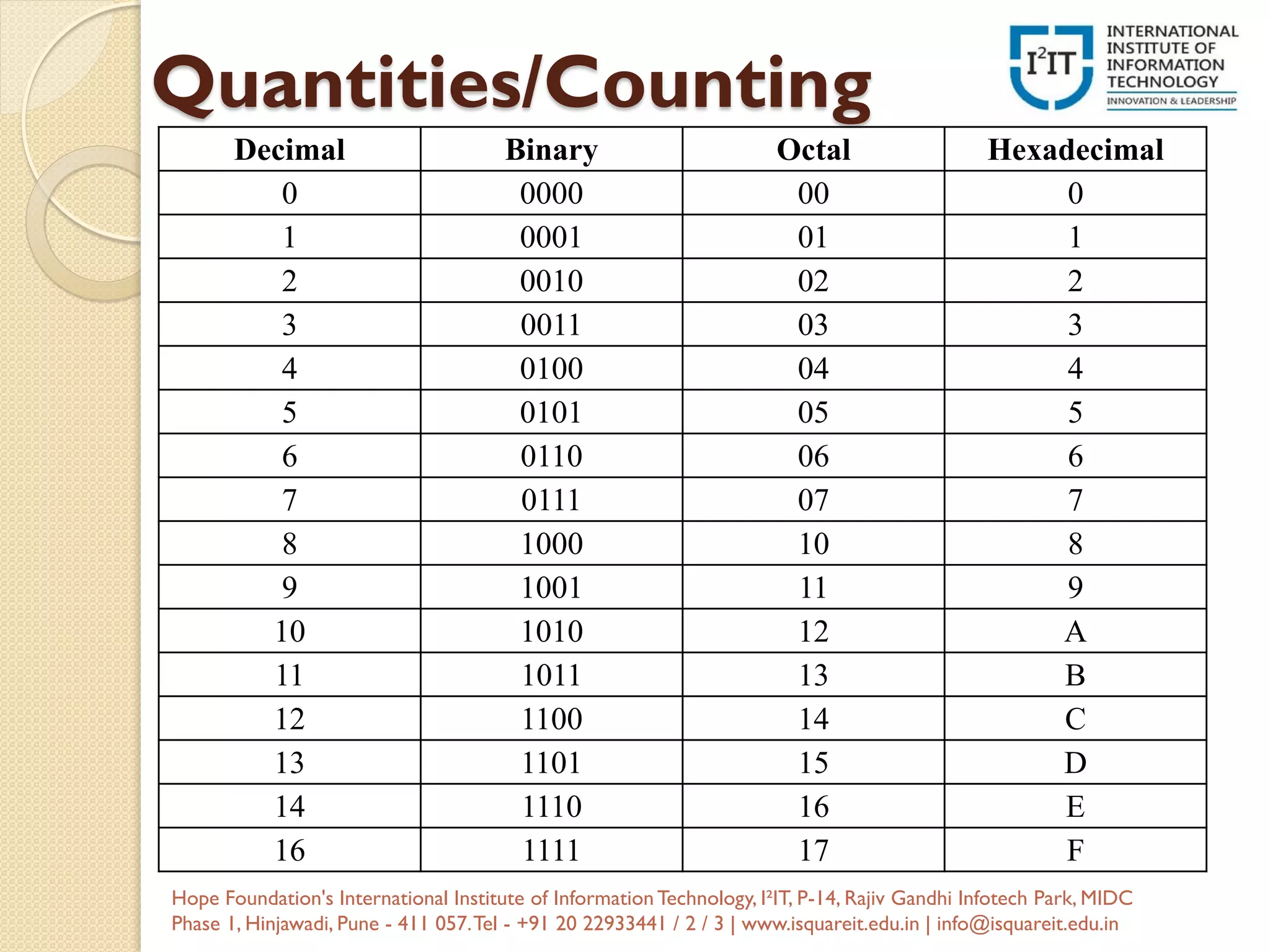
The document covers the basics of digital electronics, focusing on digital signals and binary number systems as foundational concepts. It discusses types of digital systems such as combinational and sequential logic circuits, along with logic gates and Boolean algebra principles. Additionally, the document outlines various number system conversions and representation formats, such as one's and two's complement.