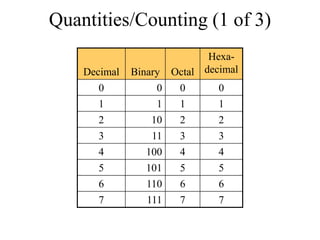
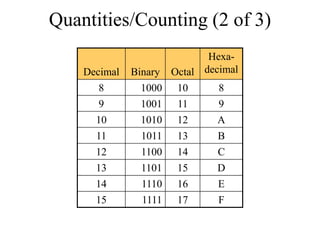
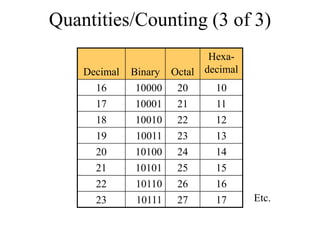
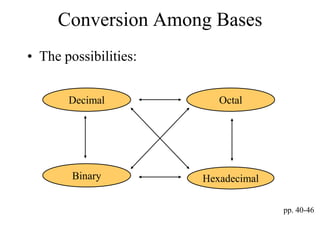
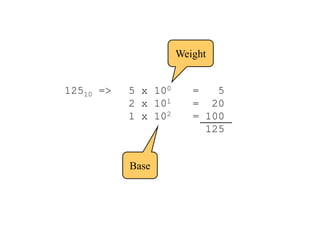
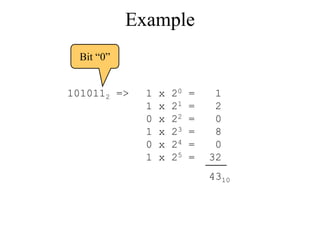
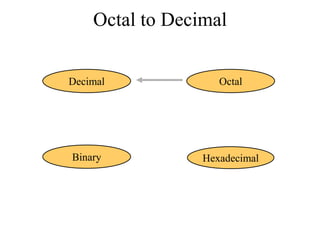
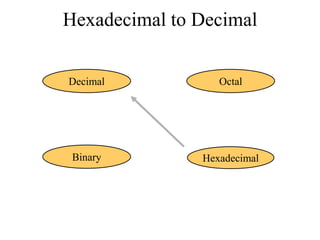
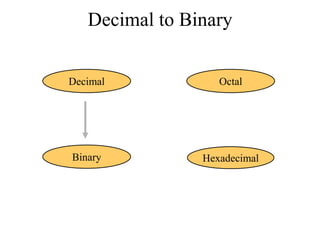
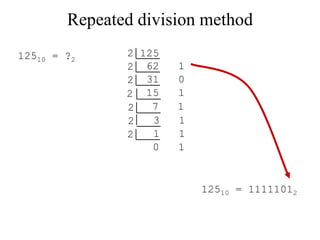
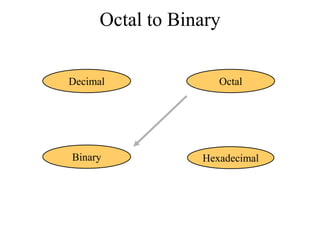
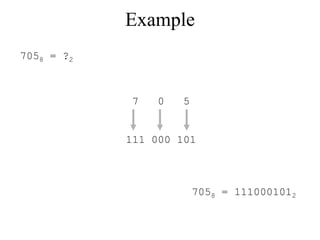
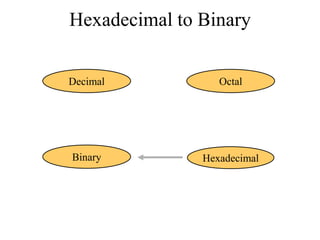
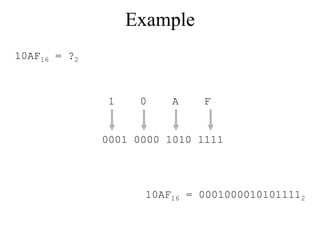
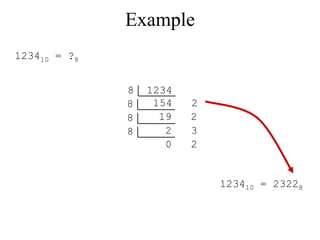
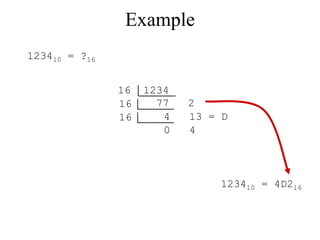
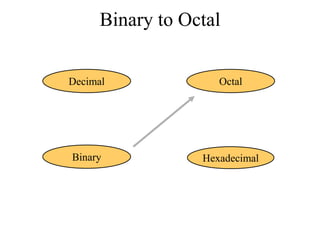
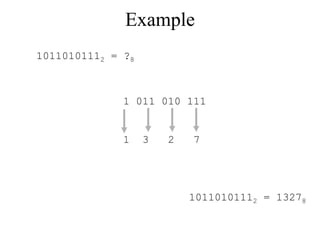
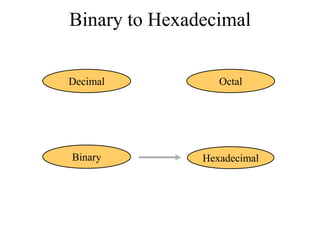
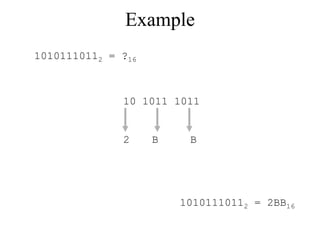
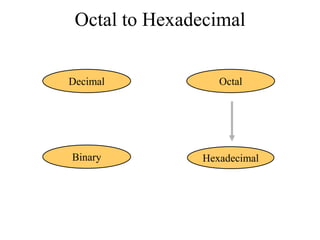
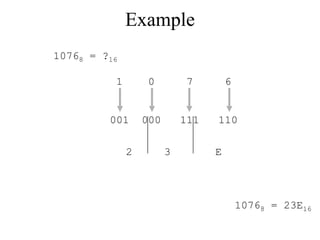
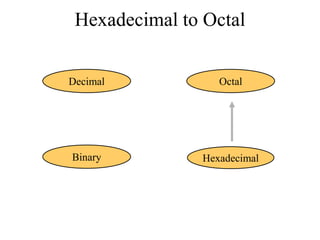
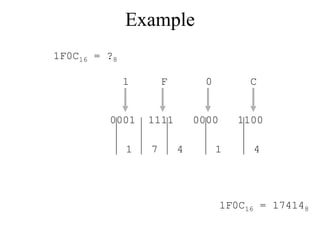
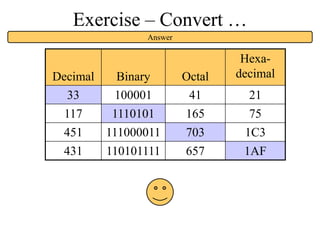
The document discusses different common number systems including decimal, binary, octal, and hexadecimal. It provides tables showing the base, symbols used, whether humans or computers use each system, and examples of counting in each system. The document also describes techniques for converting between the different number systems by multiplying or dividing place values and keeping track of remainders.

1. 1. Number Systems

2. Common Number Systems
System
Base Symbols
Used by
humans?
Used in
computers?
Decimal
10
0, 1, … 9
Yes
No
Binary
2
0, 1
No
Yes
Octal
8
0, 1, … 7
No
No
Hexadecimal
16
0, 1, … 9,
A, B, … F
No
No

3. Quantities/Counting (1 of 3)
Decimal
Binary
HexaOctal decimal
0
1
2
0
1
10
0
1
2
0
1
2
3
4
5
6
7
11
100
101
110
111
3
4
5
6
7
3
4
5
6
7

4. Quantities/Counting (2 of 3)
Decimal
Binary
HexaOctal decimal
8
9
10
1000
1001
1010
10
11
12
8
9
A
11
12
13
14
15
1011
1100
1101
1110
1111
13
14
15
16
17
B
C
D
E
F

5. Quantities/Counting (3 of 3)
Decimal
Binary
HexaOctal decimal
16
17
18
10000
10001
10010
20
21
22
10
11
12
19
20
21
22
23
10011
10100
10101
10110
10111
23
24
25
26
27
13
14
15
16
17
Etc.

6. Conversion Among Bases
• The possibilities:
Decimal
Octal
Binary
Hexadecimal
pp. 40-46

7. Quick Example
2510 = 110012 = 318 = 1916
Base

8. Decimal to Decimal (just for fun)
Decimal
Octal
Binary
Hexadecimal
Next slide…

9. Weight
12510 =>
5 x 100
2 x 101
1 x 102
Base
=
5
= 20
= 100
125

10. Binary to Decimal
Decimal
Octal
Binary
Hexadecimal

11. Binary to Decimal
• Technique
– Multiply each bit by 2n, where n is the “weight”
of the bit
– The weight is the position of the bit, starting
from 0 on the right
– Add the results

12. Example
Bit “0”
1010112 =>
1
1
0
1
0
1
x
x
x
x
x
x
20
21
22
23
24
25
=
=
=
=
=
=
1
2
0
8
0
32
4310

13. Octal to Decimal
Decimal
Octal
Binary
Hexadecimal

14. Octal to Decimal
• Technique
– Multiply each bit by 8n, where n is the “weight”
of the bit
– The weight is the position of the bit, starting
from 0 on the right
– Add the results

15. Example
7248 =>
4 x 80 =
2 x 81 =
7 x 82 =
4
16
448
46810

16. Hexadecimal to Decimal
Decimal
Octal
Binary
Hexadecimal

17. Hexadecimal to Decimal
• Technique
– Multiply each bit by 16n, where n is the
“weight” of the bit
– The weight is the position of the bit, starting
from 0 on the right
– Add the results

18. Example
ABC16 =>
C x 160 = 12 x
1 =
12
B x 161 = 11 x 16 = 176
A x 162 = 10 x 256 = 2560
274810

19. Decimal to Binary
Decimal
Octal
Binary
Hexadecimal

20. Decimal to Binary
• There are two methods that can be used to
convert decimal numbers to binary:
– Repeated subtraction method
– Repeated division method
• Both methods produce the same result and
you should use whichever one you are most
comfortable with.

21. The Repeated Subtraction method
– Step 1:
• Starting with the 1s place, write down all of
the binary place values in order until you get
to the first binary place value that is
GREATER THAN the decimal number you
are trying to convert.
1024 512 256 128 64 32 16 8 4 2 1

22. The Repeated Subtraction method
– Step 2:
• Mark out the largest place value (it just tells
us how many place values we need).
853
1024 512 256 128 64 32 16 8 4 2 1

23. The Repeated Subtraction method
• – Step 3:
• Subtract the largest place value from the
decimal number. Place a “1” under that
place value.
853 - 512 = 341
512 256 128 64 32 16 8 4 2 1
1

24. The Repeated Subtraction method
– Step 4:
• For the rest of the place values, try to
subtract each one from the previous result.
– If you can, place a “1” under that place
value.
– If you can’ t, place a “0” under that place
value.

25. The Repeated Subtraction method
• – Step 5:
• Repeat Step 4 until all of the place values
have been processed.
• The resulting set of 1s and 0s is the binary
equivalent of the decimal number you
started with.

26. The Repeated Subtraction method

27. Repeated division method
12510 = ?2
2 125
2 62
2 31
2 15
7
2
3
2
1
2
0
1
0
1
1
1
1
1
12510 = 11111012

28. Octal to Binary
Decimal
Octal
Binary
Hexadecimal

29. Octal to Binary
• Technique
– Convert each octal digit to a 3-bit equivalent
binary representation

30. Example
7058 = ?2
7
0
5
111 000 101
7058 = 1110001012

31. Hexadecimal to Binary
Decimal
Octal
Binary
Hexadecimal

32. Hexadecimal to Binary
• Technique
– Convert each hexadecimal digit to a 4-bit
equivalent binary representation

33. Example
10AF16 = ?2
1
0
A
F
0001 0000 1010 1111
10AF16 = 00010000101011112

34. Decimal to Octal
Decimal
Octal
Binary
Hexadecimal

35. Decimal to Octal
• Technique
– Divide by 8
– Keep track of the remainder

36. Example
123410 = ?8
8
8
8
8
1234
154
19
2
0
2
2
3
2
123410 = 23228

37. Decimal to Hexadecimal
Decimal
Octal
Binary
Hexadecimal

38. Decimal to Hexadecimal
• Technique
– Divide by 16
– Keep track of the remainder

39. Example
123410 = ?16
16
16
16
1234
77
4
0
2
13 = D
4
123410 = 4D216

40. Binary to Octal
Decimal
Octal
Binary
Hexadecimal

41. Binary to Octal
• Technique
– Group bits in threes, starting on right
– Convert to octal digits

42. Example
10110101112 = ?8
1 011 010 111
1
3
2
7
10110101112 = 13278

43. Binary to Hexadecimal
Decimal
Octal
Binary
Hexadecimal

44. Binary to Hexadecimal
• Technique
– Group bits in fours, starting on right
– Convert to hexadecimal digits

45. Example
10101110112 = ?16
10 1011 1011
2
B
B
10101110112 = 2BB16

46. Octal to Hexadecimal
Decimal
Octal
Binary
Hexadecimal

47. Octal to Hexadecimal
• Technique
– Use binary as an intermediary

48. Example
10768 = ?16
1
0
7
6
001
000
111
110
2
3
E
10768 = 23E16

49. Hexadecimal to Octal
Decimal
Octal
Binary
Hexadecimal

50. Hexadecimal to Octal
• Technique
– Use binary as an intermediary

51. Example
1F0C16 = ?8
1
F
0
C
0001
1111
0000
1100
1
7
4
1
4
1F0C16 = 174148

52. Exercise – Convert ...
Decimal
33
Binary
Octal
Hexadecimal
1110101
703
1AF
Don’t use a calculator!
Skip answer
Answer

53. Exercise – Convert …
Answer
Hexadecimal
Decimal
33
Binary
100001
Octal
41
117
1110101
165
75
451
111000011
703
1C3
431
110101111
657
1AF
21