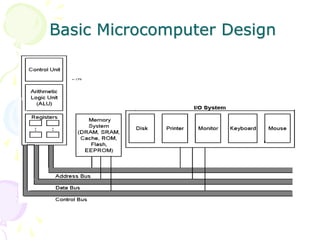
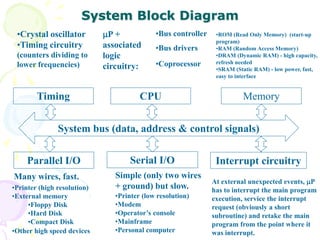
This document provides an overview of microcomputer structure and operation. It describes the basic components of a CPU including registers, control unit, and ALU. It explains the bus structure used to transfer information between components. It also details the instruction execution cycle and how instructions are fetched, decoded, and executed. Finally, it includes a system block diagram showing how various components like memory, I/O devices, and timing circuitry interface with the CPU and bus.

1. Overview on
Microcomputer Structure
and Operation
Rana Mukherji

2. Rana Mukherji
M.Tech. (Instrumentation) ,Panjab University, Chandigarh, yr 2004
Experience Around 7.5 years
Area of Interest includes Reconfigurable Computing & VLSI
Design
Professional Memberships : VLSI Society of India, Bangalore
World SystemC Community, LA
Paper Published in Conferences/ Journals – 20 Including 1 paper in
IEEE Computer Society Journal
Achievement – Rastrapati Scout Award Winner,
Won Best Paper Award at International Conference on Systemics,
Cybernetics and Informatics, Hyderabad, INDIA

3. Basic Microcomputer Design

4. Inside the CPU
• Registers – used for storing data values and addresses
• Control Unit (CU) – coordinates the sequencing of steps
involved in executing machine instructions
• Arithmetic Logic Unit (ALU) - performs arithmetic and
logical operations
• Clock – synchronizes the internal operations of the CPU
with the other system components

5. Bus Structure
• Bus - a group of parallel wires that transfer information
from one part of the computer to another.
– Control Bus – synchronizes the actions of all of the
devices attached to the system bus.
– Address Bus – passes the addresses of instructions and
data between the CPU and memory (or I/O).
– Data Bus – transfers instructions and data between the
CPU and memory (or I/O).

6. Instruction Execution Cycle
• The execution of a single machine instruction can be
divided into a sequence of individual operations called the
instruction execution cycle. Before executing, a program is
loaded into memory.
• The instruction pointer contains the address of the next
instruction. The instruction queue holds a group of
instructions about to be executed. Executing a machine
instruction requires three basic steps: fetch, decode and
execute
• Two more steps are required when the instruction uses a
memory operand: fetch operand and store output operand

7. Execution Cycle
• Fetch: The control unit fetches the instruction from the
instruction queue and increments the instruction pointer
(IP). The instruction pointer is also known as the program
counter.
• Decode: The control unit decodes the instruction’s
function to determine what the instruction will do. The
instruction’s input operands are passed to the arithmetic
logic unit (ALU), and signals are sent to the ALU
indicating the operation to be performed.
• Fetch operands: If the instruction uses an input operand
located in memory, the control unit uses a read operation to
retrieve the operand and copy it into internal registers.
Internal registers are not visible to user programs.

8. • Execute: The ALU executes the instruction using the
named registers and internal registers as operands and
sends the output to named registers and/or memory. The
ALU updates status flags providing information about the
processor state.
• Store output operand: If the output operand is in memory,
the control unit uses a write operation to store the data.

9. System Block Diagram
System bus (data, address & control signals)
Memory
Interrupt circuitrySerial I/OParallel I/O
Timing CPU
P +
associated
logic
circuitry:
•Bus controller
•Bus drivers
•Coprocessor
•ROM (Read Only Memory) (start-up
program)
•RAM (Random Access Memory)
•DRAM (Dynamic RAM) - high capacity,
refresh needed
•SRAM (Static RAM) - low power, fast,
easy to interface
•Crystal oscillator
•Timing circuitry
(counters dividing to
lower frequencies)
At external unexpected events, P
has to interrupt the main program
execution, service the interrupt
request (obviously a short
subroutine) and retake the main
program from the point where it
was interrupt.
Simple (only two wires
+ ground) but slow.
•Printer (low resolution)
•Modem
•Operator’s console
•Mainframe
•Personal computer
Many wires, fast.
•Printer (high resolution)
•External memory
•Floppy Disk
•Hard Disk
•Compact Disk
•Other high speed devices

10. Overview of Basic
Computer Mathematics
Rana Mukherji
rmukherji@icfaitech.org

11. Common Computer
Number System
System Base Symbols
Used by
humans?
Used in
computers?
Decimal 10 0, 1, … 9 Yes No
Binary 2 0, 1 No Yes
Octal 8 0, 1, … 7 No No
Hexa-
decimal
16 0, 1, … 9,
A, B, … F
No No

12. Quantities/Counting (1 of 3)
Decimal Binary Octal
Hexa-
decimal
0 0 0 0
1 1 1 1
2 10 2 2
3 11 3 3
4 100 4 4
5 101 5 5
6 110 6 6
7 111 7 7
p. 33

13. Quantities/Counting (2 of 3)
Decimal Binary Octal
Hexa-
decimal
8 1000 10 8
9 1001 11 9
10 1010 12 A
11 1011 13 B
12 1100 14 C
13 1101 15 D
14 1110 16 E
15 1111 17 F

14. Quantities/Counting (3 of 3)
Decimal Binary Octal
Hexa-
decimal
16 10000 20 10
17 10001 21 11
18 10010 22 12
19 10011 23 13
20 10100 24 14
21 10101 25 15
22 10110 26 16
23 10111 27 17 Etc.

15. Conversion Among Bases
• The possibilities:
Hexadecimal
Decimal Octal
Binary

16. Quick Example
2510 = 110012 = 318 = 1916
Base

17. Decimal to Decimal
Hexadecimal
Decimal Octal
Binary

18. 12510 => 5 x 100= 5
2 x 101= 20
1 x 102= 100
125
Base
Weight

19. Binary to Decimal
Hexadecimal
Decimal Octal
Binary

20. Binary to Decimal
• Technique
– Multiply each bit by 2n, where n is the
“weight” of the bit
– The weight is the position of the bit,
starting from 0 on the right
– Add the results

21. Example
1010112 => 1 x 20 = 1
1 x 21 = 2
0 x 22 = 0
1 x 23 = 8
0 x 24 = 0
1 x 25 = 32
4310
Bit “0”

22. Octal to Decimal
Hexadecimal
Decimal Octal
Binary

23. Octal to Decimal
• Technique
– Multiply each bit by 8n, where n is the
“weight” of the bit
– The weight is the position of the bit,
starting from 0 on the right
– Add the results

24. Example
7248 => 4 x 80 = 4
2 x 81 = 16
7 x 82 = 448
46810

25. Hexadecimal to Decimal
Hexadecimal
Decimal Octal
Binary

26. Hexadecimal to Decimal
• Technique
– Multiply each bit by 16n, where n is the
“weight” of the bit
– The weight is the position of the bit,
starting from 0 on the right
– Add the results

27. Example
ABC16 => C x 160 = 12 x 1 = 12
B x 161 = 11 x 16 = 176
A x 162 = 10 x 256 = 2560
274810

28. Decimal to Binary
Hexadecimal
Decimal Octal
Binary

29. Decimal to Binary
• Technique
– Divide by two, keep track of the
remainder
– First remainder is bit 0 (LSB, least-
significant bit)
– Second remainder is bit 1
– Etc.

30. Example
12510 = ?2
2 125
62 12
31 02
15 1
2
7 1
2
3 12
1 12
0 1
12510 = 11111012

31. Octal to Binary
Hexadecimal
Decimal Octal
Binary

32. Octal to Binary
• Technique
– Convert each octal digit to a 3-bit
equivalent binary representation

33. Example
7058 = ?2
7 0 5
111 000 101
7058 = 1110001012

34. Hexadecimal to Binary
Hexadecimal
Decimal Octal
Binary

35. Hexadecimal to Binary
• Technique
– Convert each hexadecimal digit to a 4-
bit equivalent binary representation

36. Example
10AF16 = ?2
1 0 A F
0001 0000 1010 1111
10AF16 = 00010000101011112

37. Decimal to Octal
Hexadecimal
Decimal Octal
Binary

38. Decimal to Octal
• Technique
– Divide by 8
– Keep track of the remainder

39. Example
123410 = ?8
8 1234
154 2
8
19 2
8
2 3
8
0 2
123410 = 23228

40. Decimal to Hexadecimal
Hexadecimal
Decimal Octal
Binary

41. Decimal to Hexadecimal
• Technique
– Divide by 16
– Keep track of the remainder

42. Example
123410 = ?16
123410 = 4D216
16 1234
77 216
4 13 = D16
0 4

43. Binary to Octal
Hexadecimal
Decimal Octal
Binary

44. Binary to Octal
• Technique
– Group bits in threes, starting on right
– Convert to octal digits

45. Example
10110101112 = ?8
1 011 010 111
1 3 2 7
10110101112 = 13278

46. Binary to Hexadecimal
Hexadecimal
Decimal Octal
Binary

47. Binary to Hexadecimal
• Technique
– Group bits in fours, starting on right
– Convert to hexadecimal digits

48. Example
10101110112 = ?16
10 1011 1011
2 B B
10101110112 = 2BB16

49. Octal to Hexadecimal
Hexadecimal
Decimal Octal
Binary

50. Octal to Hexadecimal
• Technique
– Use binary as an intermediary

51. Example
10768 = ?16
1 0 7 6
001 000 111 110
2 3 E
10768 = 23E16

52. Hexadecimal to Octal
Hexadecimal
Decimal Octal
Binary

53. Hexadecimal to Octal
• Technique
– Use binary as an intermediary

54. Example
1F0C16 = ?8
1 F 0 C
0001 1111 0000 1100
1 7 4 1 4
1F0C16 = 174148

55. Exercise – Convert ...
Decimal Binary Octal
Hexa-
decimal
33
1110101
703
1AF

56. Exercise – Convert …
Decimal Binary Octal
Hexa-
decimal
33 100001 41 21
117 1110101 165 75
451 111000011 703 1C3
431 110101111 657 1AF
Answer

57. Binary Addition (1 of 2)
• Two 1-bit values
pp. 36-
38
A B A + B
0 0 0
0 1 1
1 0 1
1 1 10
“two”

58. Binary Addition (2 of 2)
• Two n-bit values
– Add individual bits
– Propagate carries
– E.g.,
10101 21
+ 11001 + 25
101110 46
11

59. Multiplication (1 of 3)
• Decimal
pp. 39
35
x 105
175
000
35
3675

60. Multiplication (2 of 3)
• Binary, two 1-bit values
A B A  B
0 0 0
0 1 0
1 0 0
1 1 1

61. Multiplication (3 of 3)
• Binary, two n-bit values
– As with decimal values
– E.g., 1110
x 1011
1110
1110
0000
1110
10011010

62. Fractions
• Decimal to decima
pp. 46-
50
3.14 => 4 x 10-2 = 0.04
1 x 10-1 = 0.1
3 x 100 = 3
3.14

63. Fractions
• Binary to decimal
pp. 46-
50
10.1011 => 1 x 2-4 = 0.0625
1 x 2-3 = 0.125
0 x 2-2 = 0.0
1 x 2-1 = 0.5
0 x 20 = 0.0
1 x 21 = 2.0
2.6875

64. Fractions
• Decimal to binary
p. 50
3.14579
.14579
x 2
0.29158
x 2
0.58316
x 2
1.16632
x 2
0.33264
x 2
0.66528
x 2
1.33056
etc.
11.001001...

65. Exercise – Convert ...
Decimal Binary Octal
Hexa-
decimal
29.8
101.1101
3.07
C.82

66. Exercise – Convert …
Decimal Binary Octal
Hexa-
decimal
29.8 11101.110011… 35.63… 1D.CC…
5.8125 101.1101 5.64 5.D
3.109375 11.000111 3.07 3.1C
12.5078125 1100.10000010 14.404 C.82
Answer

67. Rana Mukherji
EXTERNAL
REPRESENTATION
Decimal BCD Code
0 0000
1 0001
2 0010
3 0011
4 0100
5 0101
6 0110
7 0111
8 1000
9 1001
Numbers
Most of numbers stored in the computer are eventually changed
by some kinds of calculations
→ Internal Representation for calculation efficiency
→ Final results need to be converted to as External Representation
for presentability
Alphabets, Symbols, and some Numbers
Elements of these information do not change in the course of processing
→ No needs for Internal Representation since they are not used
for calculations
→ External Representation for processing and presentability
Example
Decimal Number: 4-bit Binary Code
BCD(Binary Coded Decimal)

68. Rana Mukherji
OTHER DECIMAL CODES
Decimal BCD(8421) 2421 84-2-1 Excess-3
0 0000 0000 0000 0011
1 0001 0001 0111 0100
2 0010 0010 0110 0101
3 0011 0011 0101 0110
4 0100 0100 0100 0111
5 0101 1011 1011 1000
6 0110 1100 1010 1001
7 0111 1101 1001 1010
8 1000 1110 1000 1011
9 1001 1111 1111 1100 d3 d2 d1 d0: symbol in the codes
BCD: d3 x 8 + d2 x 4 + d1 x 2 + d0 x 1
 8421 code.
2421: d3 x 2 + d2 x 4 + d1 x 2 + d0 x 1
84-2-1: d3 x 8 + d2 x 4 + d1 x (-2) + d0 x (-1)
Excess-3: BCD + 3
Note: 8,4,2,-2,1,-1 in this table is the weight
associated with each bit position.
BCD: It is difficult to obtain the 9's complement.
However, it is easily obtained with the other codes listed above.
→ Self-complementing codes

69. Rana Mukherji
Example
• 709310 = ? (in BCD)
7 0 9 3
0111 0000 1001 0011

70. Rana Mukherji
BCD Addition
Decimal digits 0 through 9 represented as 0000 through 1001 in binary
Addition:
5 = 0101
3 = 0011
1000 = 8
5 = 0101
8 = 1000
1101 = 13!
Problem
when digit
sum exceeds 9
Solution: add 6 (0110) if sum exceeds 9!
5 = 0101
8 = 1000
1101
6 = 0110
1 0011 = 1 3 in BCD
9 = 1001
7 = 0111
1 0000 = 16 in binary
6 = 0110
1 0110 = 1 6 in BCD

71. Rana Mukherji
GRAY CODE
* Characterized by having their representations of the binary integers differ
in only one digit between consecutive integers
* Useful in some applications
Decimal
number
Gray Binary
g3 g2 g1 g0 b3 b2 b1 b0
0 0 0 0 0 0 0 0 0
1 0 0 0 1 0 0 0 1
2 0 0 1 1 0 0 1 0
3 0 0 1 0 0 0 1 1
4 0 1 1 0 0 1 0 0
5 0 1 1 1 0 1 0 1
6 0 1 0 1 0 1 1 0
7 0 1 0 0 0 1 1 1
8 1 1 0 0 1 0 0 0
9 1 1 0 1 1 0 0 1
10 1 1 1 1 1 0 1 0
11 1 1 1 0 1 0 1 1
12 1 0 1 0 1 1 0 0
13 1 0 1 1 1 1 0 1
14 1 0 0 1 1 1 1 0
15 1 0 0 0 1 1 1 1
4-bit Gray codes
Other Binary codes

72. Rana Mukherji
GRAY CODE - ANALYSIS
Letting gngn-1 ... g1 g0 be the (n+1)-bit Gray code
for the binary number bnbn-1 ... b1b0
gi = bi  bi+1 , 0  i  n-1
gn = bn
and
bn-i = gn  gn-1  . . .  gn-i
bn = gn

73. Rana Mukherji
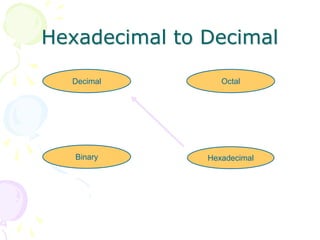
CHARACTER REPRESENTATION
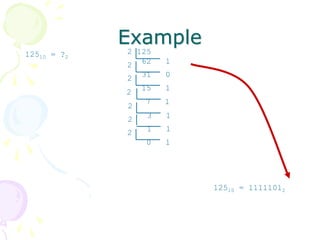
ASCIIASCII (American Standard Code for Information Interchange) Code
Other Binary codes
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
NUL
SOH
STX
ETX
EOT
ENQ
ACK
BEL
BS
HT
LF
VT
FF
CR
SO
SI
SP
!
“
#
$
%
&
‘
(
)
*
+
,
-
.
/
0
1
2
3
4
5
6
7
8
9
:
;
<
=
>
?
@
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
[
]
m
n
‘
a
b
c
d
e
f
g
h
I
j
k
l
m
n
o
P
q
r
s
t
u
v
w
x
y
z
{
|
}
~
DEL
0 1 2 3 4 5 6 7
DLE
DC1
DC2
DC3
DC4
NAK
SYN
ETB
CAN
EM
SUB
ESC
FS
GS
RS
US
LSB
(4 bits)
MSB (3 bits)

74. Rana Mukherji
CONTROL CHARACTER REPRESENTAION
(ASCII)
NUL Null
SOH Start of Heading (CC)
STX Start of Text (CC)
ETX End of Text (CC)
EOT End of Transmission (CC)
ENQ Enquiry (CC)
ACK Acknowledge (CC)
BEL Bell
BS Backspace (FE)
HT Horizontal Tab. (FE)
LF Line Feed (FE)
VT Vertical Tab. (FE)
FF Form Feed (FE)
CR Carriage Return (FE)
SO Shift Out
SI Shift In
DLE Data Link Escape (CC)
(CC) Communication Control
(FE) Format Effector
(IS) Information Separator
DC1 Device Control 1
DC2 Device Control 2
DC3 Device Control 3
DC4 Device Control 4
NAK Negative Acknowledge (CC)
SYN Synchronous Idle (CC)
ETB End of Transmission Block (CC)
CAN Cancel
EM End of Medium
SUB Substitute
ESC Escape
FS File Separator (IS)
GS Group Separator (IS)
RS Record Separator (IS)
US Unit Separator (IS)
DEL Delete

75. Rana Mukherji
000 001 010 011 100 101 110 111
0000 NULL DLE 0 @ P ` p
0001 SOH DC1 ! 1 A Q a q
0010 STX DC2 " 2 B R b r
0011 ETX DC3 # 3 C S c s
0100 EDT DC4 $ 4 D T d t
0101 ENQ NAK % 5 E U e u
0110 ACK SYN & 6 F V f v
0111 BEL ETB ' 7 G W g w
1000 BS CAN ( 8 H X h x
1001 HT EM ) 9 I Y i y
1010 LF SUB * : J Z j z
1011 VT ESC + ; K [ k {
1100 FF FS , < L l |
1101 CR GS - = M ] m }
1110 SO RS . > N ^ n ~
1111 SI US / ? O _ o DEL

76. Rana Mukherji
000 001 010 011 100 101 110 111
0000 NULL DLE 0 @ P ` p
0001 SOH DC1 ! 1 A Q a q
0010 STX DC2 " 2 B R b r
0011 ETX DC3 # 3 C S c s
0100 EDT DC4 $ 4 D T d t
0101 ENQ NAK % 5 E U e u
0110 ACK SYN & 6 F V f v
0111 BEL ETB ' 7 G W g w
1000 BS CAN ( 8 H X h x
1001 HT EM ) 9 I Y i y
1010 LF SUB * : J Z j z
1011 VT ESC + ; K [ k {
1100 FF FS , < L l |
1101 CR GS - = M ] m }
1110 SO RS . > N ^ n ~
1111 SI US / ? O _ o DEL
Most significant bit
Least significant bit

77. Rana Mukherji
000 001 010 011 100 101 110 111
0000 NULL DLE 0 @ P ` p
0001 SOH DC1 ! 1 A Q a q
0010 STX DC2 " 2 B R b r
0011 ETX DC3 # 3 C S c s
0100 EDT DC4 $ 4 D T d t
0101 ENQ NAK % 5 E U e u
0110 ACK SYN & 6 F V f v
0111 BEL ETB ' 7 G W g w
1000 BS CAN ( 8 H X h x
1001 HT EM ) 9 I Y i y
1010 LF SUB * : J Z j z
1011 VT ESC + ; K [ k {
1100 FF FS , < L l |
1101 CR GS - = M ] m }
1110 SO RS . > N ^ n ~
1111 SI US / ? O _ o DEL
e.g., ‘a’ = 1100001

78. Rana Mukherji
95 Graphic codes
000 001 010 011 100 101 110 111
0000 NULL DLE 0 @ P ` p
0001 SOH DC1 ! 1 A Q a q
0010 STX DC2 " 2 B R b r
0011 ETX DC3 # 3 C S c s
0100 EDT DC4 $ 4 D T d t
0101 ENQ NAK % 5 E U e u
0110 ACK SYN & 6 F V f v
0111 BEL ETB ' 7 G W g w
1000 BS CAN ( 8 H X h x
1001 HT EM ) 9 I Y i y
1010 LF SUB * : J Z j z
1011 VT ESC + ; K [ k {
1100 FF FS , < L l |
1101 CR GS - = M ] m }
1110 SO RS . > N ^ n ~
1111 SI US / ? O _ o DEL

79. Rana Mukherji
33 Control codes
000 001 010 011 100 101 110 111
0000 NULL DLE 0 @ P ` p
0001 SOH DC1 ! 1 A Q a q
0010 STX DC2 " 2 B R b r
0011 ETX DC3 # 3 C S c s
0100 EDT DC4 $ 4 D T d t
0101 ENQ NAK % 5 E U e u
0110 ACK SYN & 6 F V f v
0111 BEL ETB ' 7 G W g w
1000 BS CAN ( 8 H X h x
1001 HT EM ) 9 I Y i y
1010 LF SUB * : J Z j z
1011 VT ESC + ; K [ k {
1100 FF FS , < L l |
1101 CR GS - = M ] m }
1110 SO RS . > N ^ n ~
1111 SI US / ? O _ o DEL

80. Rana Mukherji
Alphabetic codes
000 001 010 011 100 101 110 111
0000 NULL DLE 0 @ P ` p
0001 SOH DC1 ! 1 A Q a q
0010 STX DC2 " 2 B R b r
0011 ETX DC3 # 3 C S c s
0100 EDT DC4 $ 4 D T d t
0101 ENQ NAK % 5 E U e u
0110 ACK SYN & 6 F V f v
0111 BEL ETB ' 7 G W g w
1000 BS CAN ( 8 H X h x
1001 HT EM ) 9 I Y i y
1010 LF SUB * : J Z j z
1011 VT ESC + ; K [ k {
1100 FF FS , < L l |
1101 CR GS - = M ] m }
1110 SO RS . > N ^ n ~
1111 SI US / ? O _ o DEL

81. Rana Mukherji
Numeric codes
000 001 010 011 100 101 110 111
0000 NULL DLE 0 @ P ` p
0001 SOH DC1 ! 1 A Q a q
0010 STX DC2 " 2 B R b r
0011 ETX DC3 # 3 C S c s
0100 EDT DC4 $ 4 D T d t
0101 ENQ NAK % 5 E U e u
0110 ACK SYN & 6 F V f v
0111 BEL ETB ' 7 G W g w
1000 BS CAN ( 8 H X h x
1001 HT EM ) 9 I Y i y
1010 LF SUB * : J Z j z
1011 VT ESC + ; K [ k {
1100 FF FS , < L l |
1101 CR GS - = M ] m }
1110 SO RS . > N ^ n ~
1111 SI US / ? O _ o DEL

82. Rana Mukherji
000 001 010 011 100 101 110 111
0000 NULL DLE 0 @ P ` p
0001 SOH DC1 ! 1 A Q a q
0010 STX DC2 " 2 B R b r
0011 ETX DC3 # 3 C S c s
0100 EDT DC4 $ 4 D T d t
0101 ENQ NAK % 5 E U e u
0110 ACK SYN & 6 F V f v
0111 BEL ETB ' 7 G W g w
1000 BS CAN ( 8 H X h x
1001 HT EM ) 9 I Y i y
1010 LF SUB * : J Z j z
1011 VT ESC + ; K [ k {
1100 FF FS , < L l |
1101 CR GS - = M ] m }
1110 SO RS . > N ^ n ~
1111 SI US / ? O _ o DEL
Punctuation, etc.

83. Rana Mukherji
“Hello, world” Example
=
=
=
=
=
=
=
=
=
=
=
=
Binary
01001000
01100101
01101100
01101100
01101111
00101100
00100000
01110111
01100111
01110010
01101100
01100100
Hexadecimal
48
65
6C
6C
6F
2C
20
77
67
72
6C
64
Decimal
72
101
108
108
111
44
32
119
103
114
108
100
H
e
l
l
o
,
w
o
r
l
d
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=

84. END of Chapter 1
Next we begin with
Digital Logic Devices for
Microprocessor System
Designs