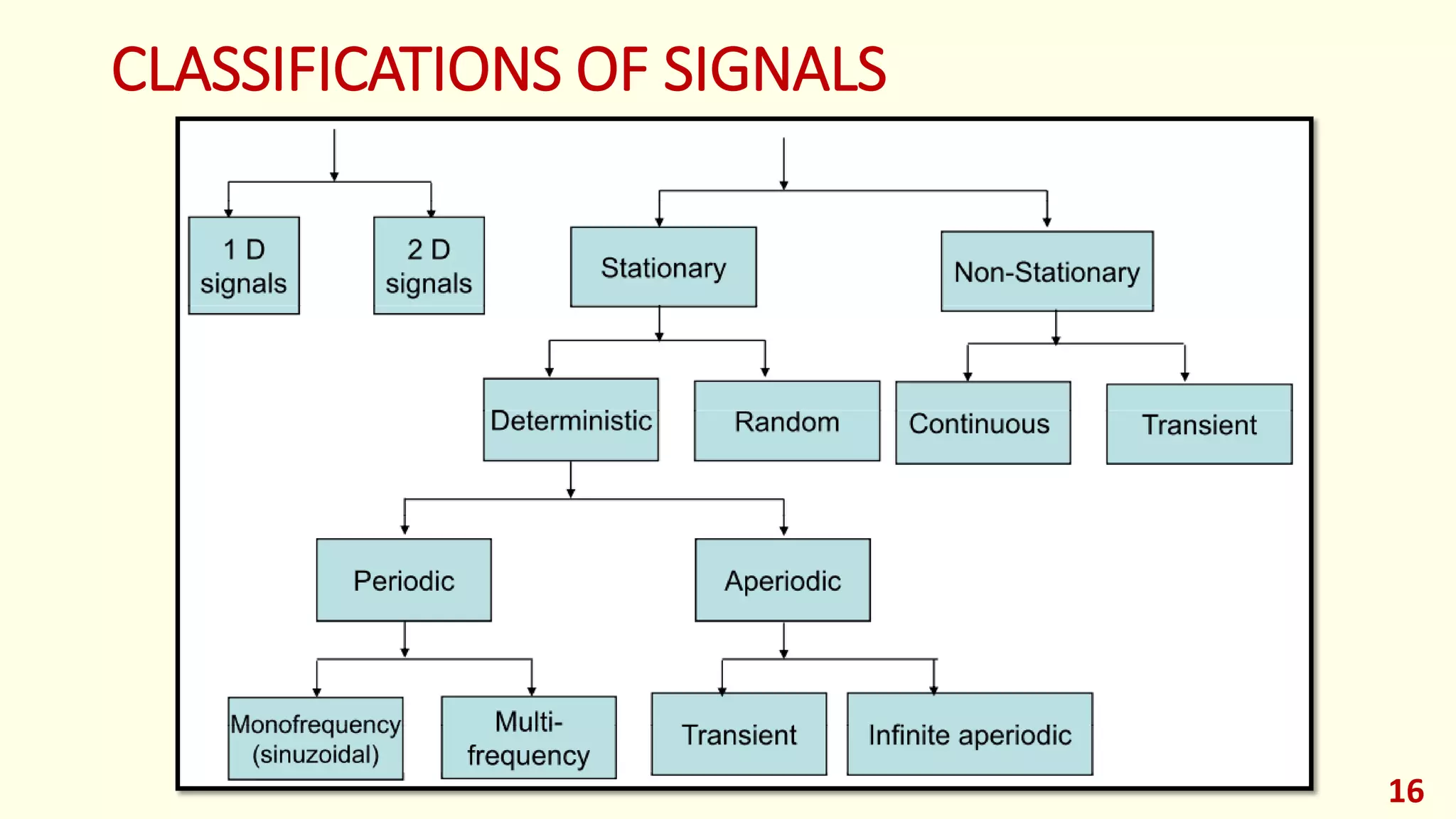
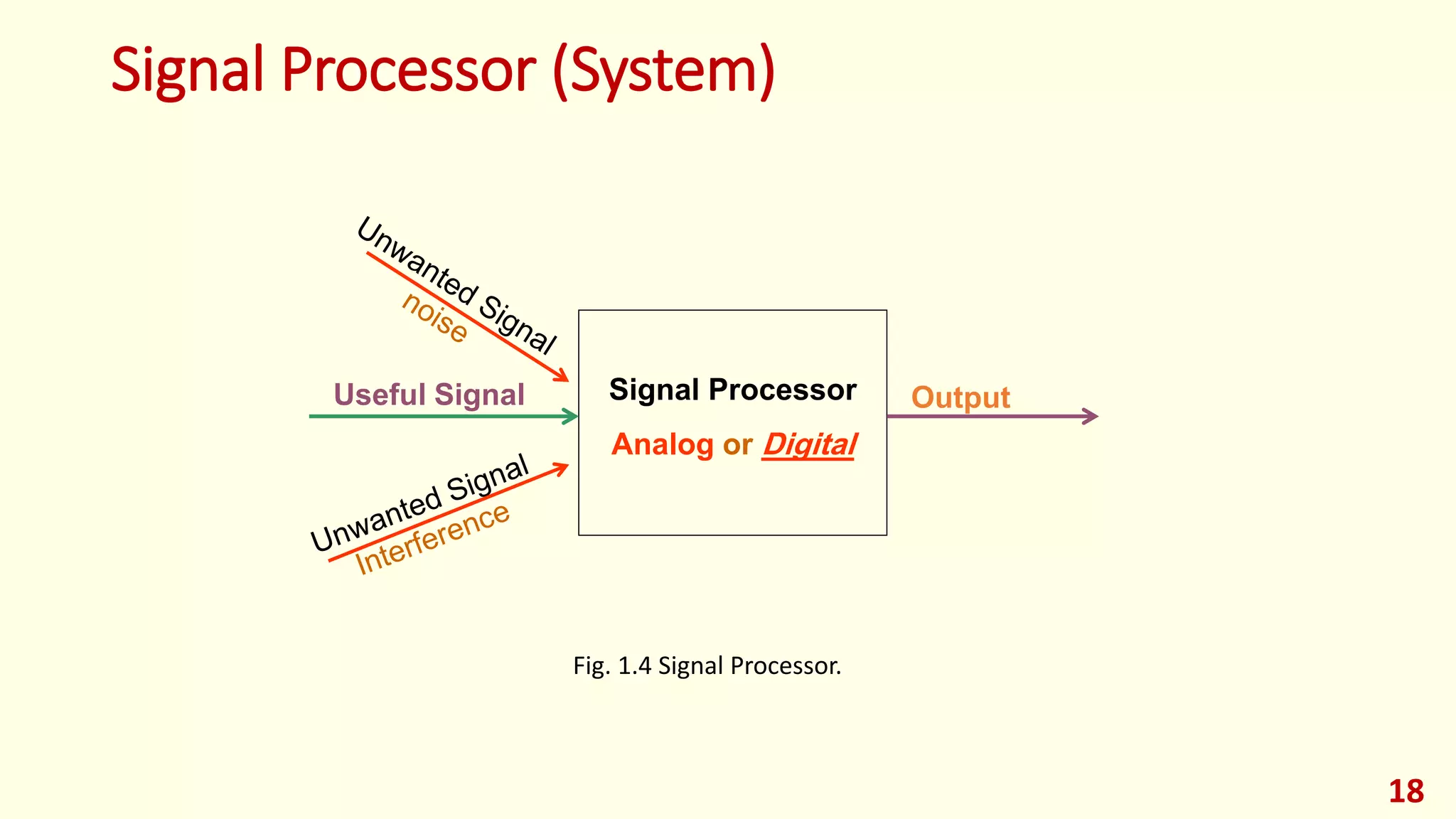
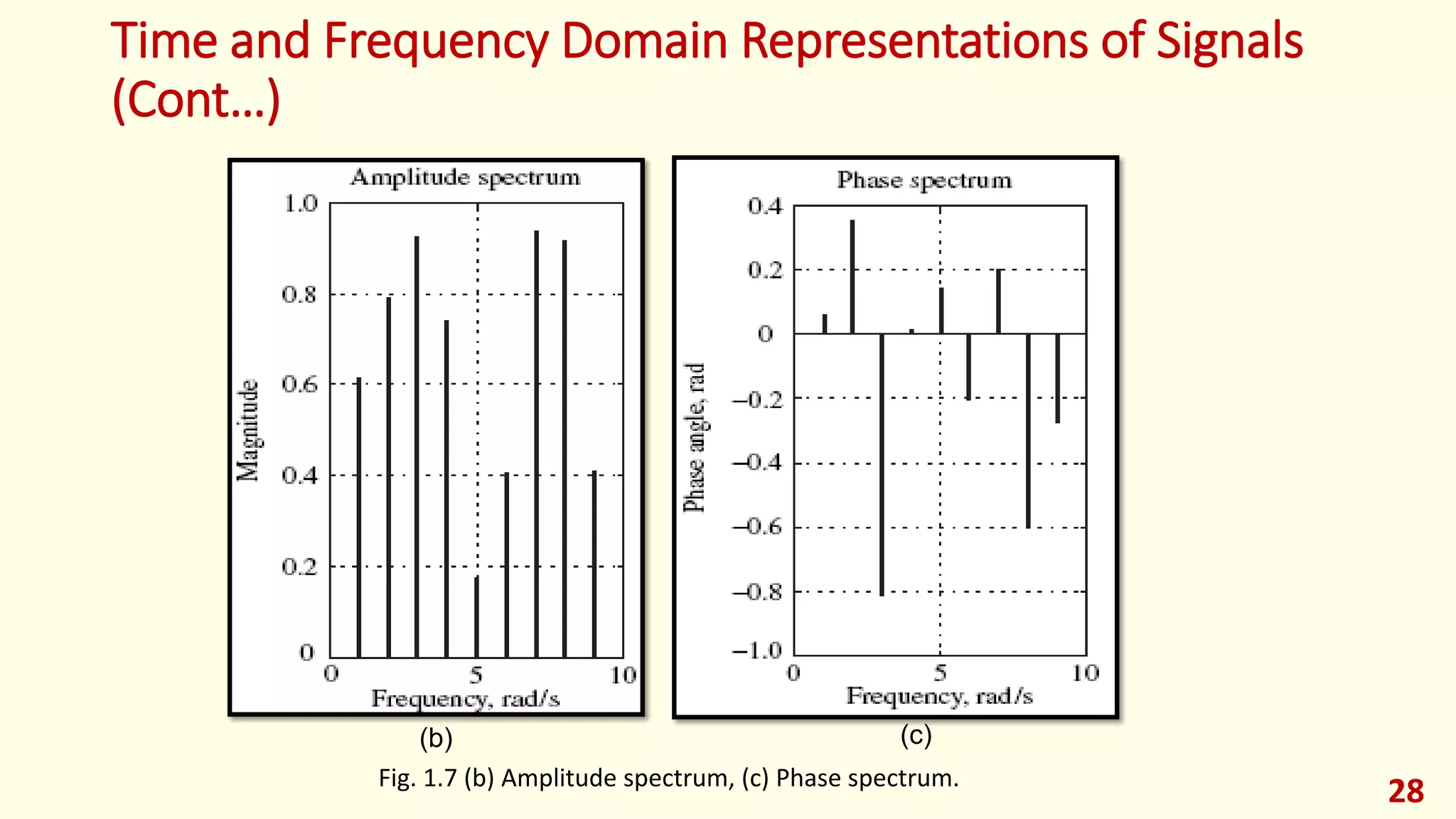
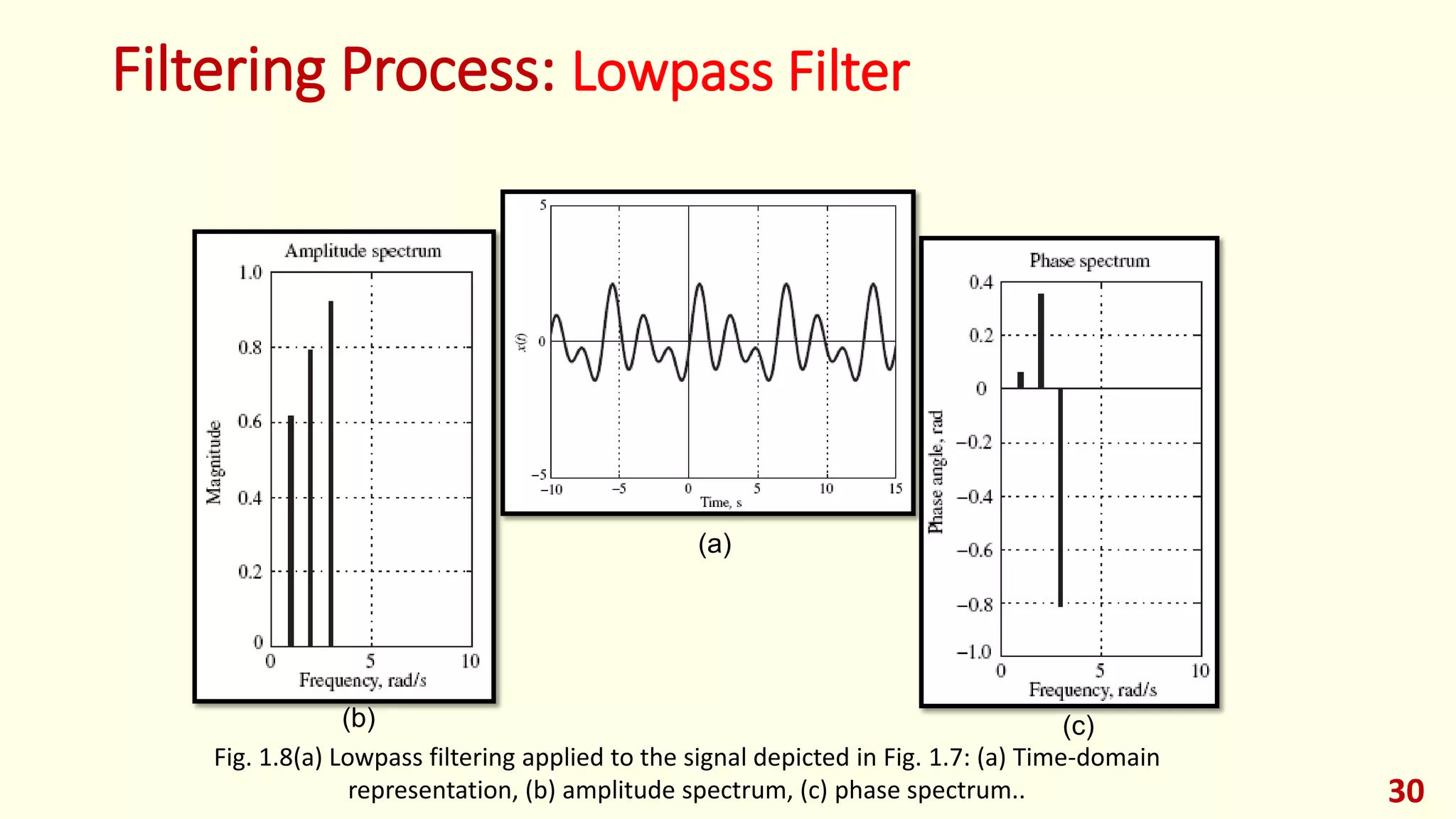
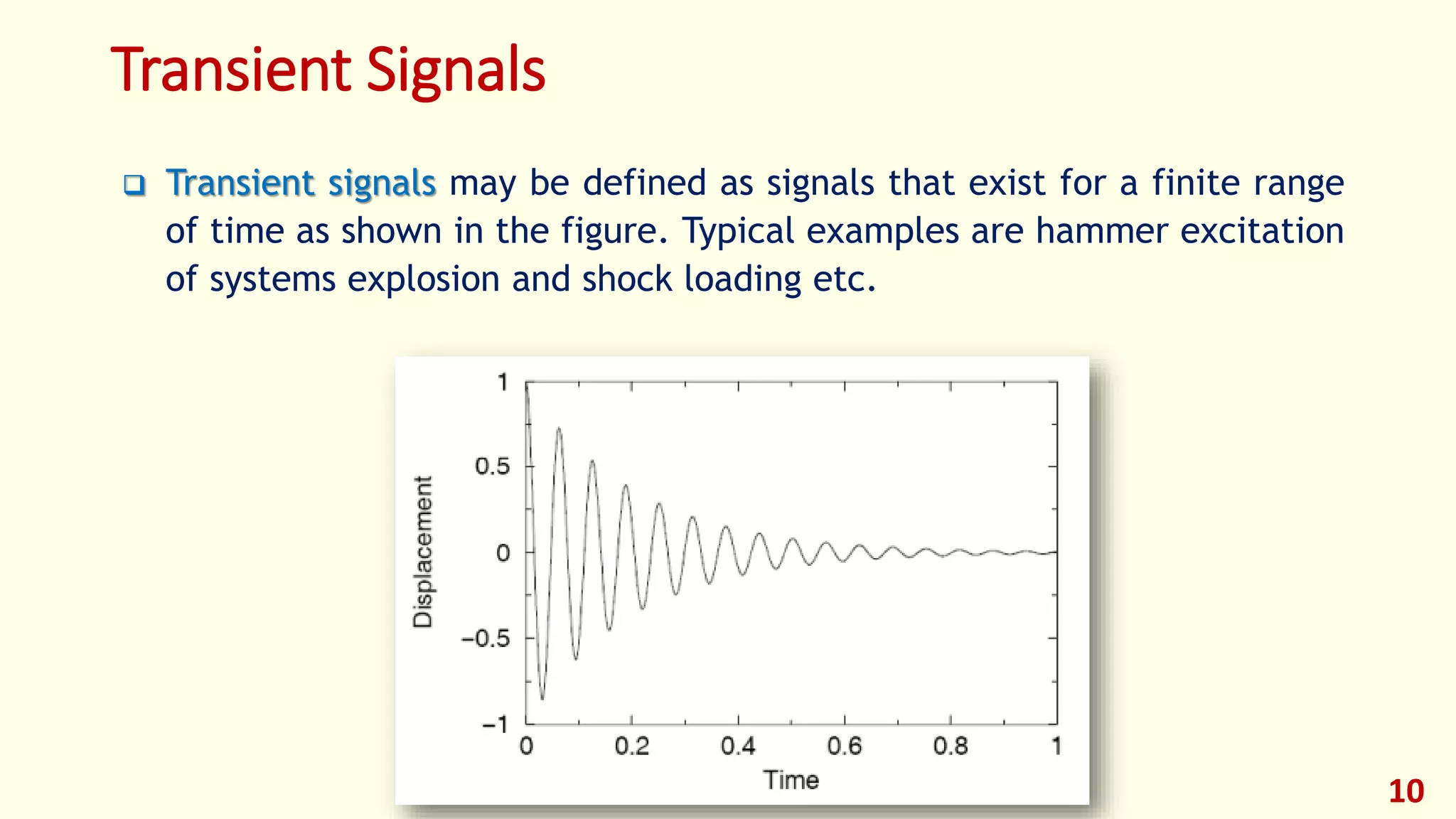
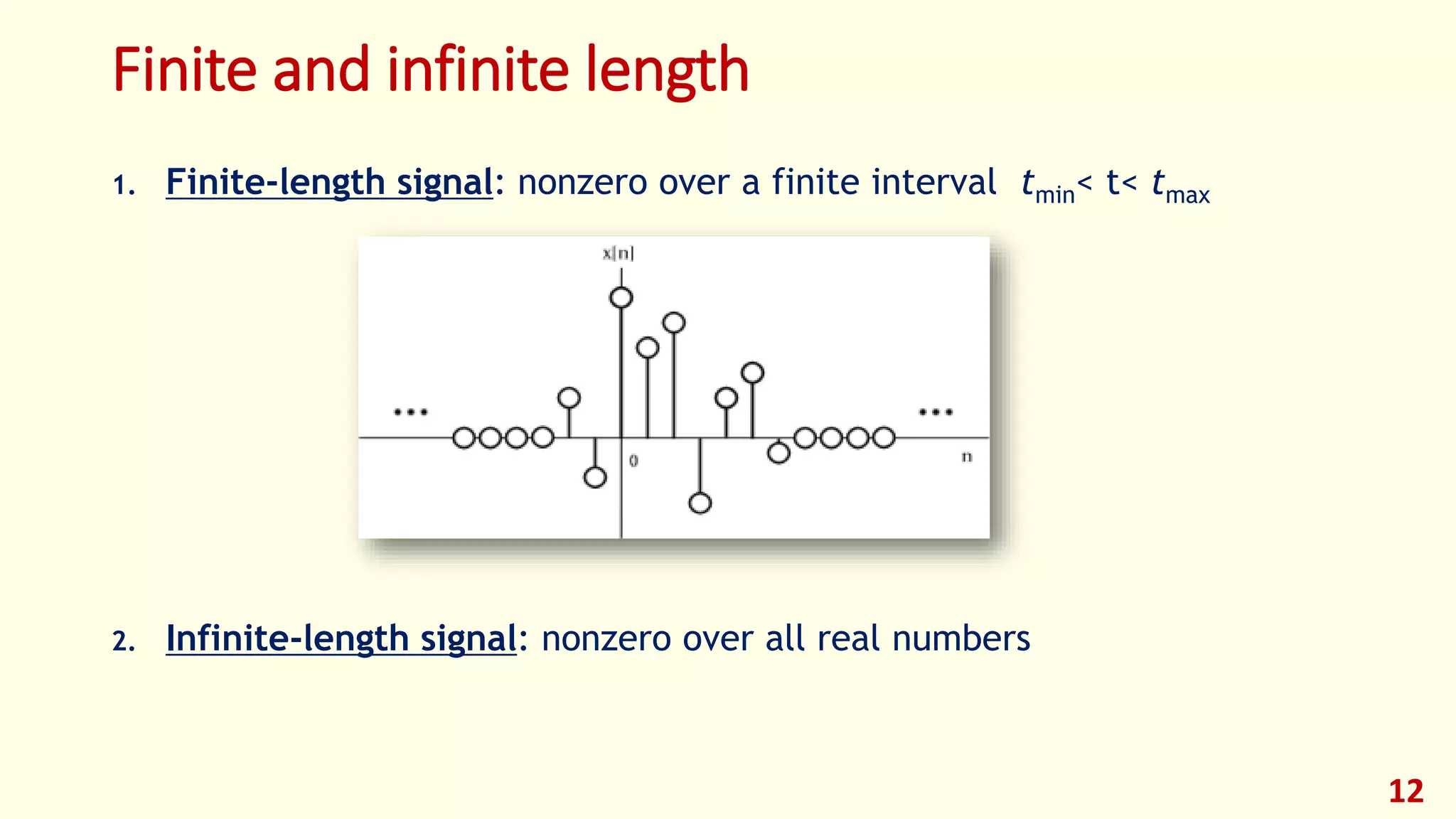
This lecture provides an introduction to digital signal processing. It defines what a signal is and discusses different types of signals including analog, discrete-time, and digital signals. It also covers signal classifications such as deterministic vs random, stationary vs non-stationary, and finite vs infinite length signals. The lecture then discusses analog signal processing systems and digital signal processing systems as well as transformations between time and frequency domains. It provides an overview of pros and cons of analog vs digital signal processing and examples of applications of digital signal processing.

1. LECTURE (1)
Introduction to Digital Signal Processing
‫ر‬َ‫ـد‬ْ‫ق‬‫ِـ‬‫ن‬،،،‫لما‬‫اننا‬ ‫نصدق‬ْْ‫ق‬ِ‫ن‬‫ر‬َ‫د‬
Amr E. Mohamed
Faculty of Engineering - Helwan University

2. Introduction
 Objectives:
 what is a signal
 What is Signal Processing
• Analog Signal Processing System
• Digital Signal Processing System
 Time and Frequency Domain Representations of Signals
 Brief introduction to MATLAB.
2

3. Fundamentals of Signals
 Signal (flow of information):
 Generally convey information about the state or behavior of a physical phenomena.
 Measured quantity that varies with time (or position)
 Electrical signal received from a transducer (Microphone, Thermometer,
Accelerometer, Antenna, etc.)
 Electrical signal that controls a process
 Signal:
 Signal is defined as any physical quantity that varies with Time, Space, or any other
independent variables. For Example, the functions
 Example:
 𝑠1(𝑡) = 5𝑡 or 𝑠1(𝑡) = 5𝑡2  one variable
 𝑆(𝑥, 𝑦) = 3𝑥 + 4𝑥𝑦 + 6𝑥2
 two variables x and y
3

4. Overview of Signal Processing: Signal Classifications
4
Fig. 1.1 Signal Classifications
Signal is a representation of physical quantity or phenomenon
Deterministic Signals Random Signals
Time Domain Representation
t is the independent variable
Frequency Domain Representation
f is the independent variable
Representation
Continuous
Discrete
Continuous
Discrete

5. Continuous-Time versus Discrete-Time Signals
1) Continuous-Time signal or analog signal: are defined for every value
of time and they take on values in the continuous interval (a,b).
 Analog Signal
 Continuous in time.
 Amplitude may take on any value in the continuous range of (-∞, ∞).
 Analog Processing
 Differentiation, Integration, Filtering, Amplification.
 Differential Equations
 Implemented via passive or active electronic circuitry.
5

6. Continuous-Time versus Discrete-Time Signals
2) Discrete-Time signals: are defined only at certain specific value of
time.
 Continuous in Amplitude but Discrete in Time
 Only defined for certain time instances.
 Can be obtained from analog signals via sampling.
6

7. 3) Digital Signal: is the signal that takes on values from a finite set of
possible values.
 Discrete in Amplitude & Discrete in Time.
 Can be obtained from Discrete signals via quantization.
7
Continuous-Time versus Discrete-Time Signals

8. Sampling Process
 Discrete-time signals are often generated from corresponding continuous-time
signals through the use of an analog-to-digital (A/D) interface. An A/D
interface typically comprises three components, namely, a sampler, a
quantizer, and an encoder as depicted in Fig. 1.3(a).
 Similarly, continuous-time signals can be obtained by using a digital-to-analog
(D/A) interface. The D/A interface comprises two modules, a decoder and a
smoothing device as depicted in Fig. 1.3(b).
8Fig. 1.3 Sampling system: (a) A/D interface, (b) D/A interface.
(SNR) dB= 6.02 n + 4.77

9. Deterministic versus Random Signals
1) Deterministic Signal: Any signal whose past,
present and future values are precisely
known without any uncertainty.
2) Random Signal: A signal in which cannot be
approximated by a formula to a reasonable
degree of accuracy (i.e. noise).
 The ‘shhhh’ sound is a good example that is
rather easy to observe using a microphone
and oscilloscope.
 Random signals are characterized by
analyzing the statistical characteristics
across an ensemble of records.
9

10. Transient Signals
 Transient signals may be defined as signals that exist for a finite range
of time as shown in the figure. Typical examples are hammer excitation
of systems explosion and shock loading etc.
10

11. Stationary versus Nonstationary Signals
 Stationary signals are those whose average properties do not change
with time Stationary signals have constant parameters to change with
time.
 Nonstationary signals have time dependent parameters. In an engine
excited vibration where the engines speed varies with time; the
fundamental period changes with time as well as with the corresponding
dynamic loads that cause vibration.
11

12. Finite and infinite length
1. Finite-length signal: nonzero over a finite interval tmin< t< tmax
2. Infinite-length signal: nonzero over all real numbers
12

13. Multi-channel & Multidimensional Signals
 A signal is described by a function of one or more independent
variables. The value of function can be real-valued Scalar, a complex-
valued, or perhaps a vector.
 Real-Valued Signal
 Complex-Valued Signal
 Vector Signal
tAts 3sin)(1 
tjtAAets tj

3sin3cos)( 3
2 











)(
)(
)(
)(
3
2
1
3
ts
ts
ts
tS
13

14. Multi-channel & Multidimensional Signals
1) Multi-channel Signals
 Signals are generated by multiple source or multiple sensor. This signals, can
represented in vector form.
 Example: ECG (Electrocardiogram) are often used 3-channel and 12-
channel.
14

15. Multi-channel & Multidimensional Signals
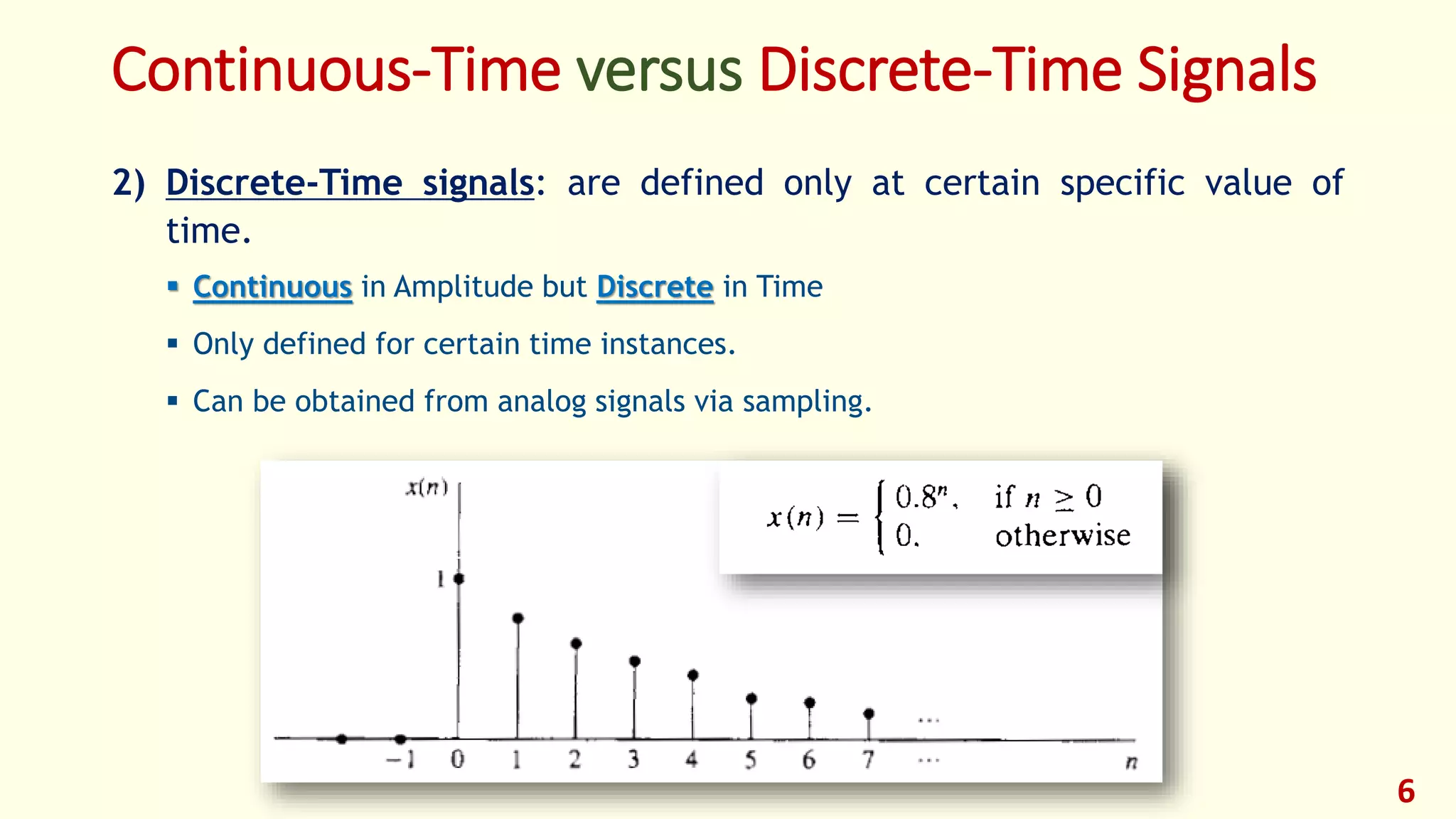
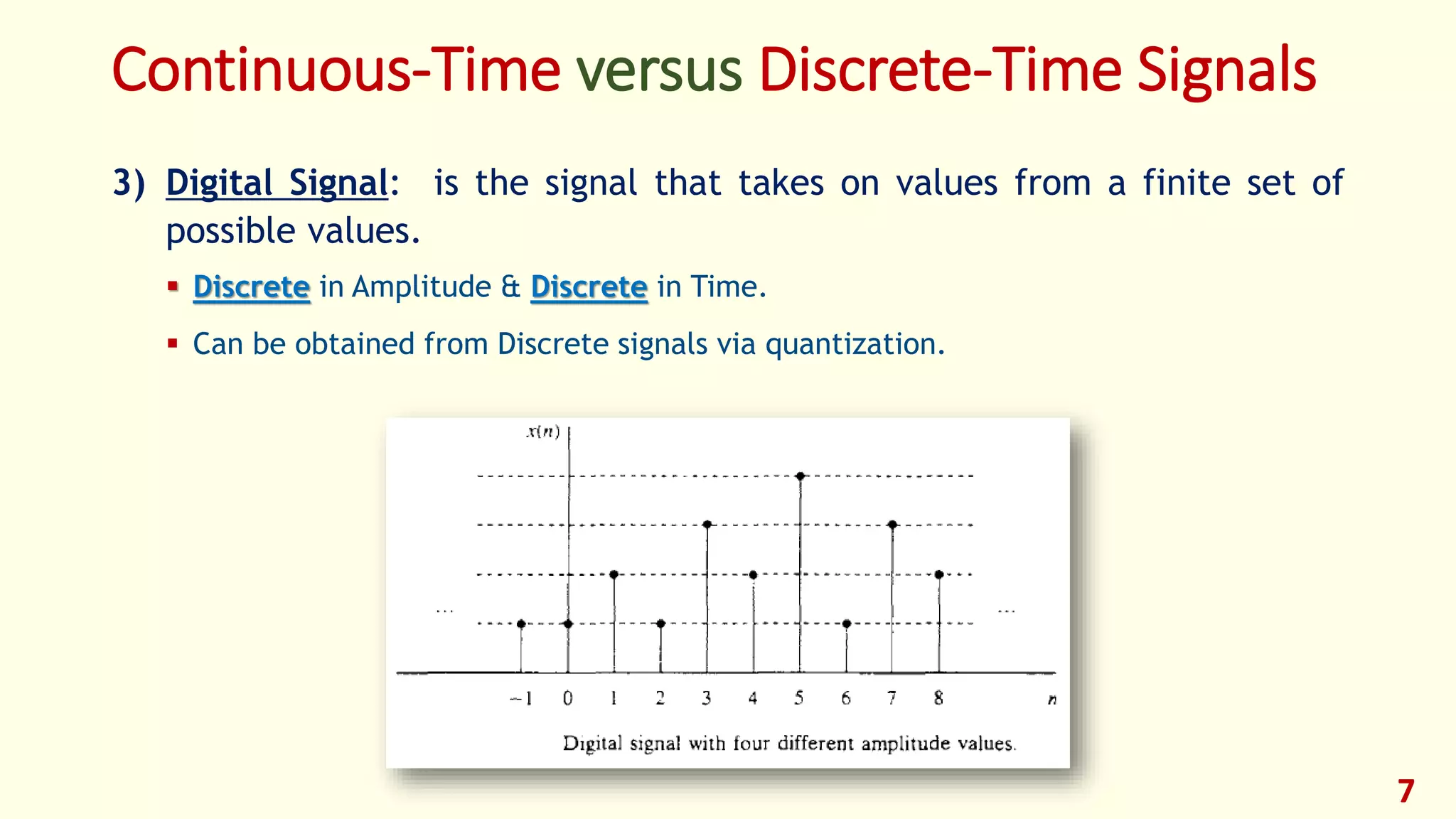
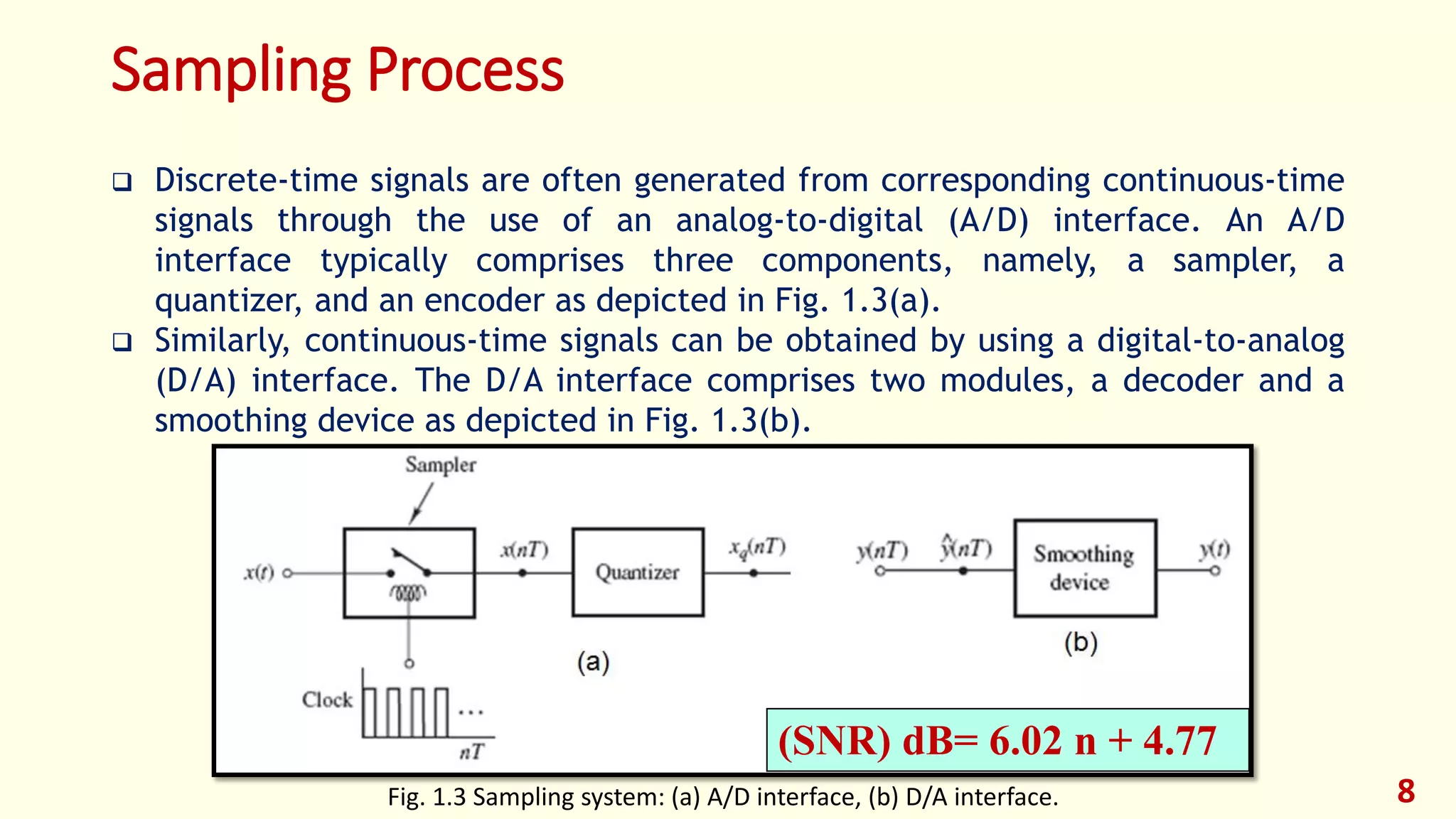
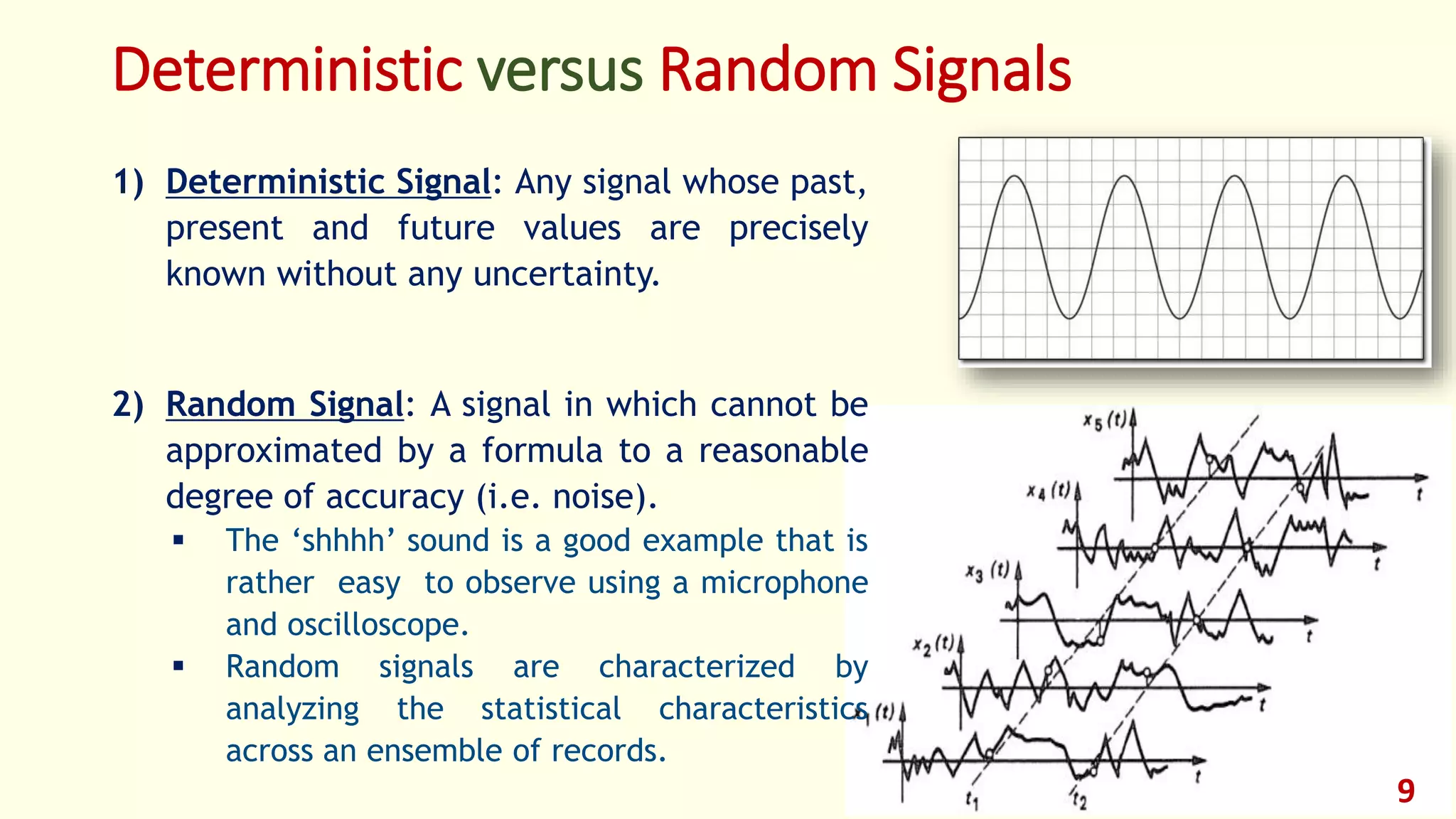
2) Multidimensional Signals:
 If the signal is a function of a single independent variable, the signal called a
one-dimensional signal.
 On the other hand , a signal called M-dimensional if its value is a function of M
independent variables.
 The gray picture is an example of a 2-dimensional signal, the brightness or the
intensity I(x,y) at each point is a function of 2 independent variables.
 The black & white TV picture [I(x,y,t)]: is a “3-Dimensional” since the
brightness is a function of time.
 The color TV picture: is a multi-channel/multidimensional signal.











),,(
),,(
),,(
),,(
tyxI
tyxI
tyxI
tyxI
b
g
r
15

16. CLASSIFICATIONS OF SIGNALS
16

17. What is Signal Processing
 Signals may have to be transformed in order to
 Amplify or filter out embedded information
 Detect patterns
 Prepare the signal to survive a transmission channel
 Undo distortions contributed by a transmission channel
 Compensate for sensor deficiencies
 Find information encoded in a different domain.
 To do so, we also need:
 Methods to measure, characterize, model, and simulate signals.
 Mathematical tools that split common channels and transformations into easily
manipulated building blocks.
17

18. Signal Processor (System)
18
Fig. 1.4 Signal Processor.
Signal Processor
Analog or Digital
OutputUseful Signal

19. Analog Signal Processing
 ℎ(𝑡): The System Impulse Response
 𝐻(𝑠): The System Transfer Function
 𝐻(Ω): The System Frequency Response
 Analogue signal processing is achieved by using analogue components
such as:
 Resistors.
 Capacitors.
 Inductors.
)(tx
)(sX
)(*)()( txthty 
)(.)()( sXsHsY 
Analog
input
Signal
Analog
output
Signal
Analog
Signal
Processor
19
)(X )(.)()(  XHY

20. Limitations of Analog Signal Processing
 Accuracy limitations due to
 Component tolerances
 Undesired nonlinearities
 Limited repeatability due to
 Tolerances
 Changes in environmental conditions
• Temperature
• Vibration
 Sensitivity to electrical noise
 Limited dynamic range for voltage and currents
 Inflexibility to changes
 Difficulty of implementing certain operations
 Nonlinear operations
 Time-varying operations
 Difficulty of storing information
20

21. Digital Signal Processing
 ℎ(𝑛): The System Impulse Response (Weighted Sequence)
 𝐻(𝑧): The System Transfer Function
 𝐻 𝑝𝑓(𝑠) : Prefilter (Band-limited – Reduce noise)
 𝐻𝑟𝑐(𝑠) : reconstruction filter (smoothing)
 Analog/digital and digital/analog converters, CPU, DSP, ASIC, FPGA
 Digital signal processing techniques are now so powerful that sometimes it is extremely
difficult, if not impossible, for analogue signal processing to achieve similar
performance.
 Examples:
 FIR filter with linear phase.
 Adaptive filters.
)(nx
)(zX
)(*)()(ˆ nxnhnx 
)(.)()(ˆ zXzHzX 
)(sH pf )(sHrc
)(tx
)(sX
)(ˆ tx
)(ˆ sX
Digital
Signal
Processor
ADC DAC
21

22. Pros and Cons of Digital Signal Processing
 Pros
 It is easy to Change, Correct, or Update applications (software changes).
 Accuracy can be controlled by choosing word length
 Repeatable
 Sensitivity to electrical noise is minimal
 Dynamic range can be controlled using floating point numbers
 Flexibility can be achieved with software implementations
 Non-linear and time-varying operations are easier to implement
 Digital storage is cheap
 Digital information can be encrypted for security
 Small size.
 Development time.
 Power consumption.
 Cost, cheaper than analog.
22

23. Pros and Cons of Digital Signal Processing
 Cons
 Sampling causes loss of information
 A/D and D/A requires mixed-signal hardware
 Limited speed of processors
 Quantization and round-off errors
 Discrete time processing artifacts (aliasing, delay)
 Dan require significantly more power (battery, cooling)
 Digital clock and switching (Synchronization)
23

24. Signal Processing
 Humans are the most advanced signal processors
 speech and pattern recognition, speech synthesis,…
 We encounter many types of signals in various applications
 Electrical signals: voltage, current, magnetic and electric fields,…
 Mechanical signals: velocity, force, displacement,…
 Acoustic signals: sound, vibration,…
 Other signals: pressure, temperature,…
 Most real-world signals are analog
 They are continuous in time and amplitude
 Convert to voltage or currents using sensors and transducers
 Analog circuits process these signals using
 Resistors, Capacitors, Inductors, Amplifiers,…
 Analog signal processing examples
 Audio processing in FM radios
 Video processing in traditional TV sets
24

25. DSP is Everywhere
 Sound applications
 Compression, enhancement, special effects, synthesis, recognition, echo cancellation,…
 Cell Phones, MP3 Players, Movies, Dictation, Text-to-speech,…
 Communication
 Modulation, coding, detection, equalization, echo cancellation,…
 Cell Phones, dial-up modem, DSL modem, Satellite Receiver,…
 Automotive
 ABS, GPS, Active Noise Cancellation, Cruise Control, Parking,…
 Medical
 Magnetic Resonance, Tomography, Electrocardiogram,…
 Military
 Radar, Sonar, Space photographs, remote sensing,…
 Image and Video Applications
 DVD, JPEG, Movie special effects, video conferencing,…
 Mechanical
 Motor control, process control, oil and mineral prospecting,…
25

26. Time and Frequency Domain Representations of Signals
 Signals have so far been represented in terms of functions of time, i.e., x(t) or x(nT). In
many situations, it is useful to represent signals in terms of functions of frequency using
Fourier transform or Fourier series.
 For example, a continuous-time periodic signal made up of a sum of sinusoidal
components such as:
can be fully described by two sets, say:
And
that describe the amplitudes and phase angles of the sinusoidal components present in
the signal. Sets A() and () can be referred to as the amplitude spectrum and phase
spectrum of the signal, respectively, for obvious reasons, and can be represented by
tables or graphs that give the amplitude and phase angle associated with each frequency.
26
)sin()(
9
1
kk
k
k tAtx   

 9...,,2,1:)(  kforAA kk 
 9...,,2,1:)(  kforkk 

27. Time and Frequency Domain Representations of Signals (Cont…)
 For example, if Ak and k in Eq. (1.1) assume the numerical values given
by Table 1.1, then x(t) can be represented in the time domain by the
graph in Fig. 1.7(a) and in the frequency domain by Table 1.1 or by the
graphs in Fig. 1.7(b) and (c).
27Fig. 1.7(a) Time-domain representation.Table 1.1 Parameters of signal in Eq. (1.1)

28. Time and Frequency Domain Representations of Signals
(Cont…)
28Fig. 1.7 (b) Amplitude spectrum, (c) Phase spectrum.
(b) (c)

29. Filtering Process
 Filtering can be used to select one or more desirable and
simultaneously reject one or more undesirable bands of frequency
components, or simply frequencies. They include different types:
1. Lowpass filters select a band of preferred low frequencies and reject a
band of undesirable high frequencies from the frequencies present in
the signal depicted in Fig. 1.7, as illustrated in Fig. 1.8.
2. Highpass filters select a band of preferred high frequencies and reject
a band of undesirable low frequencies as illustrated in Fig. 1.9.
3. Bandpass filters select a band of frequencies and reject low and high
frequencies as illustrated in Fig. 1.10.
4. Bandstop filters to reject a band of frequencies but select low
frequencies and high frequencies as illustrated in Fig. 1.11.
29

30. Filtering Process: Lowpass Filter
30
Fig. 1.8(a) Lowpass filtering applied to the signal depicted in Fig. 1.7: (a) Time-domain
representation, (b) amplitude spectrum, (c) phase spectrum..
(b) (c)
(a)

31. Filtering Process: Highpass Filter
31
Fig. 1.9(a) Highpass filtering applied to the signal depicted in Fig. 1.3: (a) Time-domain
representation, (b) amplitude spectrum, (c) phase spectrum..
(b)
(c)
(a)

32. Filtering Process: Bandpass Filter
32
Fig. 1.10(a) Bandpass filtering applied to the signal depicted in Fig. 1.3: (a) Time-domain
representation, (b) amplitude spectrum, (c) phase spectrum..
(b) (c)
(a)

33. Filtering Process: Bandstop Filter
33
Fig. 1.11(a) Bandstop filtering applied to the signal depicted in Fig. 1.3: (a) Time-domain
representation, (b) amplitude spectrum, (c) phase spectrum..
(b) (c)
(a)

34. 34