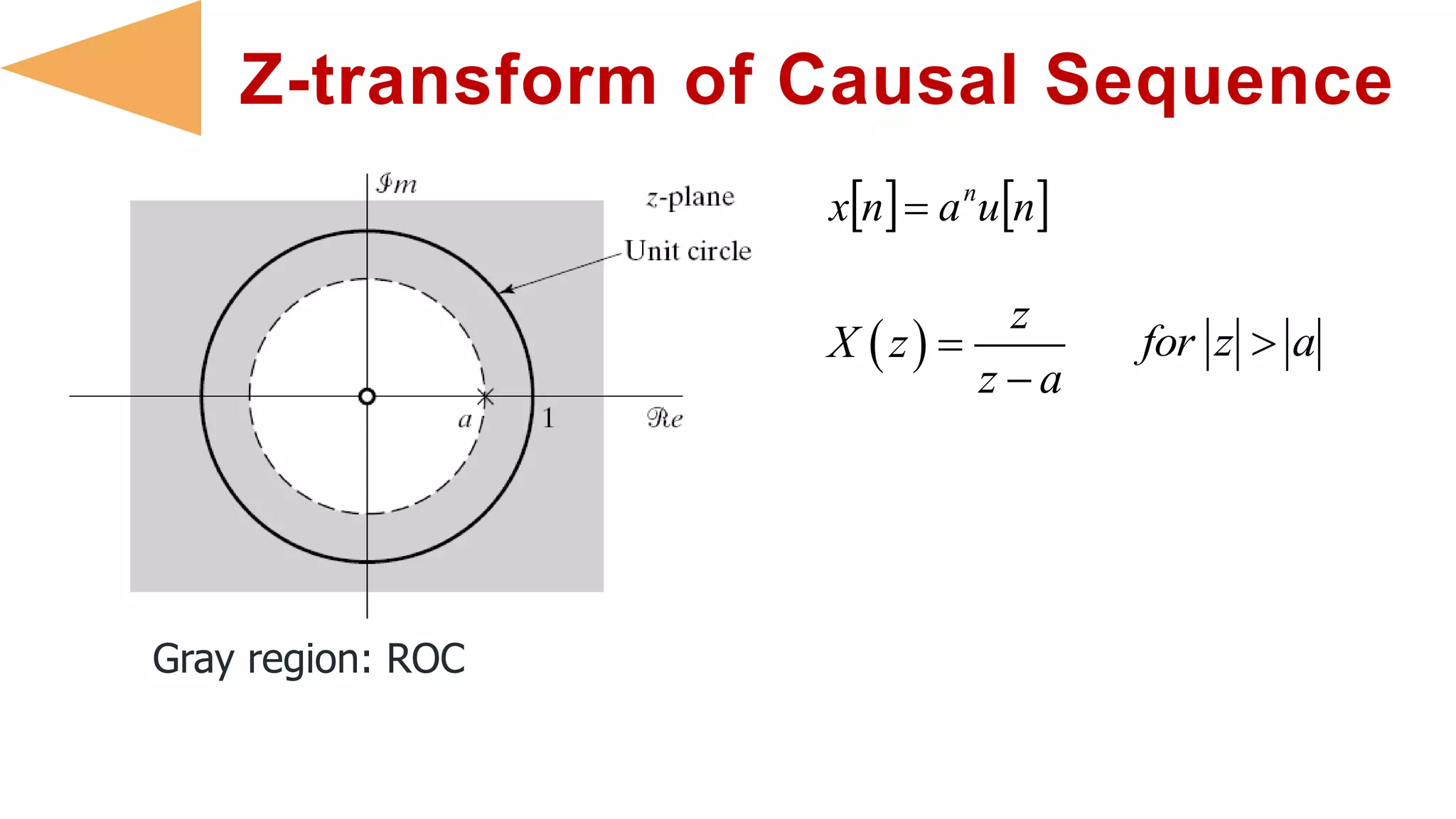
This document discusses the Z-transform, which converts a discrete-time signal into a complex frequency domain representation. Some key points: - The Z-transform provides a technique for analyzing and designing discrete time signals and systems, representing them in the complex Z-plane. It has advantages over other transforms like allowing stability analysis. - The region of convergence (ROC) is the set of Z-plane values where the Z-transform is finite. ROCs cannot contain poles and must be connected. Causal sequences have an exterior ROC, anti-causal an interior one. - Z-transforms characterize discrete time signals and linear time-invariant systems completely. Properties include how ROCs restrict poles, and transformations

1. Z-Transform
Brach: Electronics & Communication Engineering (11)
Semester: B.E (2nd year - 4th Semester)
Subject: Signal & System (SS)
GTU Subject Code: 3141005
Prepared By:-
Darshan Bhatt
Assistant Professor, EC Dept.
AIT, Ahmedabad, Gujarat

2. Content
 Introduction
 Advantages of Z-transform
 Definition of Z-transform
 ROC of Z-transform
 Properties of ROC
 Z-transform of causal sequence
 Z-transform of anti-causal sequence
 Properties of Z-transform
 Some important Z-transform Pairs

3. • In mathematics and signal processing, the Z-transform converts a discrete-
time signal, which is a sequence of real or complex numbers, into a complex
frequency-domain representation.
• The basic idea now known as the Z-transform was known to Laplace, and it
was re-introduced in 1947 by W. Hurewicz and others as a way to treat
sampled-data control systems used with radar.
• Z- transform provides a valuable technique for analysis and design of
discrete time signals and discrete time LTI systems.
Introduction

4. • The Z-transform has real and imaginary parts like Fourier transform.
• A plot of imaginary part versus real part is called as Z-plane or complex Z-
plane.
• The poles and zeros of discrete time systems (DTS) are plotted in Z-plane.
• We can also check the stability of the DTS using pole-zero plot.
Introduction

5. • Discrete time signals and LTI systems can be completely characterized by Z-
transform.
• The stability of LTI System can be determined by Z-transform.
• Mathematical calculations are reduced using Z-transform.
• DFT and FT can be determined by calculating Z-transform of the signal.
• Entire family of digital filter can be obtained one prototype design using Z-
transform.
• The solution of differential equations can be simplified using Z-transform.
Advantages of Z-transform

6. Definition: Z-transform
Bilateral or two-sided Z-transform:
Unilateral or single-sided Z-transform:

7. ROC of the Z-transform
Region of convergence (ROC):
• ROC of X(Z) is set for all the values of Z for which X(Z) attains a
finite value.

8. Properties of ROC
• The ROC is a ring, whose center is at origin.
• ROC cannot contain any pole.
• The ROC must be a connected region.
• If ROC of X(Z) includes unit circle then and then only the Fourier
transform of DT Sequence x(n) converges.
• For a finite duration sequence x(n); ROC is entire Z-plane except
Z=0 and Z=infinite.
• If x(n) is causal then ROC is the exterior part of the circle having
radius ‘a’ and for anti-causal ROC is the interior part of the same.

9. Z-transform of Causal Sequence
Determine the z-transform, including the ROC in z-plane and a sketch of
the pole-zero-plot, for sequence:
   nuanx n

   1
0 0
nn n
n n
X z a z az
 
 
 
  
az:polez:zero  0
Solution:
ROC: 1
1az or z a
 
1
1
1
z
az z a
 
 

10. Z-transform of Causal Sequence
Gray region: ROC
   nuanx n

 
z
X z
z a


for z a

11. Z-transform of Anti-Causal Sequence
Determine the z-transform, including the ROC in z-plane and a sketch of
the pole-zero-plot, for sequence:
   
1
1n n n n
n n
X z a u n z a z
 
 
 
      
   1 nuanx n
,z a
 1
1 1
nn n
n n
a z a z
 
 
 
    
1
1
1
a z z
a z z a


  
 
: 0 :zero z pole z a 
Solution:
ROC:

12. Z-transform of Anti-Causal Sequence
 
z
X z
z a


for z a
   1 nuanx n

13. Properties of Z-transform

14. Some important Z-transform Pairs

15. THANK YOU