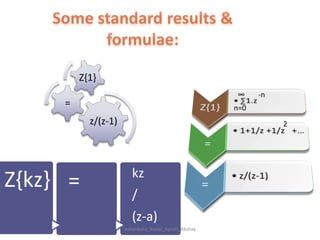
Z-transforms can be used to evaluate discrete functions, similar to how Laplace transforms are used for continuous functions. The z-transform of a discrete function f(n) is defined as the sum of f(n) multiplied by z to the power of -n, from n=0 to infinity. Some standard z-transform results include formulas for exponential, sinusoidal, and polynomial functions. Z-transforms have properties of linearity and shifting, and can be used to solve differential equations with constant coefficients and in applications of signal processing.

1. Z-TransformsAakankshaThakreAyushAgrawalKunalAgrawalAkshayPhadnisAakanksha_Kunal_Ayush_Akshay

2. Introduction:Just like Laplace transforms are used for evaluation of continuous functions, Z-transforms can be used for evaluating discrete functions.Z-Transforms are highly expedient in discrete analysis ,Which form the basis of communication technology.Definition:If a function f(n) is defined for discreet values ( n=0,+1 or -1 , +2 or -2,etc ) & f(n)=0 for n<0,then z-transform of the function is defined asZ{f(n)}=∞∑-nf(n) z=F(z)n=0Aakanksha_Kunal_Ayush_Akshay

3. Some standard results & formulae: -n∞ n=02Aakanksha_Kunal_Ayush_Akshay

4. Z{}n=aZ / (z-a)Z{n}=-aZ / (z+a)2Z{n}= z / (z-1)Z{1/n!}=e1/zZ{sin nф}= zSinф / (z -2zcosф +1 )22 2Z{Cosnф}= z- zCosф / (z -2zCosф + 1)Aakanksha_Kunal_Ayush_Akshay

5. Properties:Linearity: -Z{a f(n)+b g(n)}=a Z{f(n)}+b Z{g(n)}Damping rule:-Z{a f(n)} = F(z/a)Multiplication by positive integer n :-Z{n f(n)}= -z d/dz ( F(z) )Aakanksha_Kunal_Ayush_Akshay

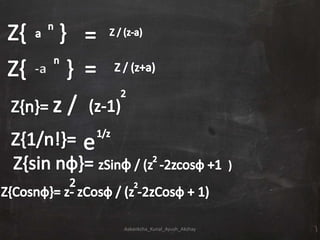
6. Initial value theorem:-f(0)= lim F(z)Z∞Final value theorem:-f(∞)= lim f(n) = lim (z-1) F(z)n∞ Z1Shifting Theorem:-Z{ f (n+k) }= z [ F(z) - ∑ f(i) z ]K-i-iKi=0Aakanksha_Kunal_Ayush_Akshay

7. Division by n property:-∞∫Z{f(n)/n}=F(z)/zdzZDivision by n+k property:-∞∫kZ{f(n) /(n+k)}=ZK+1F(z)/ (Z)dzzAakanksha_Kunal_Ayush_Akshay

8. Applications of Z-TransformsThe field of signal processing is essentially a field of signal analysis in which they are reduced to their mathematical components and evaluated. One important concept in signal processing is that of the Z-Transform, which converts unwieldy sequences into forms that can be easily dealt with. Z-Transforms are used in many signal processing systemsZ-transforms can be used to solve differential equations with constant coefficients.Aakanksha_Kunal_Ayush_Akshay

9. Derivation of the z-TransformThe z-transform is the discrete-time counterpart of the Laplace transform. In thissection we derive the z-transform from the Laplace transform a discrete-time signal.Aakanksha_Kunal_Ayush_Akshay

10. The Laplace transform X(s), of a continuous-time signal x(t), is given by the integral ∞ -stX(s) = ∫ x(t) e dt0-where the complex variable s=a +jω, and the lower limit of t=0− allows the possibilitythat the signal x(t) may include an impulse. The inverse Laplace transform is definedby:-a+j∞stX(t) = ∫ X(s) e dsa-j∞Aakanksha_Kunal_Ayush_Akshay

11. where a is selected so that X(s) is analytic (no singularities) for s>a. The ztransformcan be derived from Eq. by sampling the continuous-time input signalx(t). For a sampled signal x(mTs), normally denoted as x(m) assuming the samplingperiod Ts=1, the Laplace transform Eq. becomes∞s-smX(e ) = ∑ x(m) em=0Aakanksha_Kunal_Ayush_Akshay

12. Substituting the variable e to the power s in Eq. with thevariable z we obtain the one-sided ztransform∞-mX(z) = ∑ x(m) zm = 0The two-sided z-transform is defined as:-∞-mX(z) = ∑ x(m) zm = -∞Aakanksha_Kunal_Ayush_Akshay

13. The Relationship Between the Laplace, the Fourier, andthe z-Transforms :-The Laplace transform, the Fourier transform and the z-transform are closely related inthat they all employ complex exponential as their basis function. For right-sidedsignals (zero-valued for negative time index) the Laplace transform is a generalisation of the Fourier transform of a continuous-time signal, and the z-transform is ageneralisation of the Fourier transform of a discrete-time signal.Aakanksha_Kunal_Ayush_Akshay