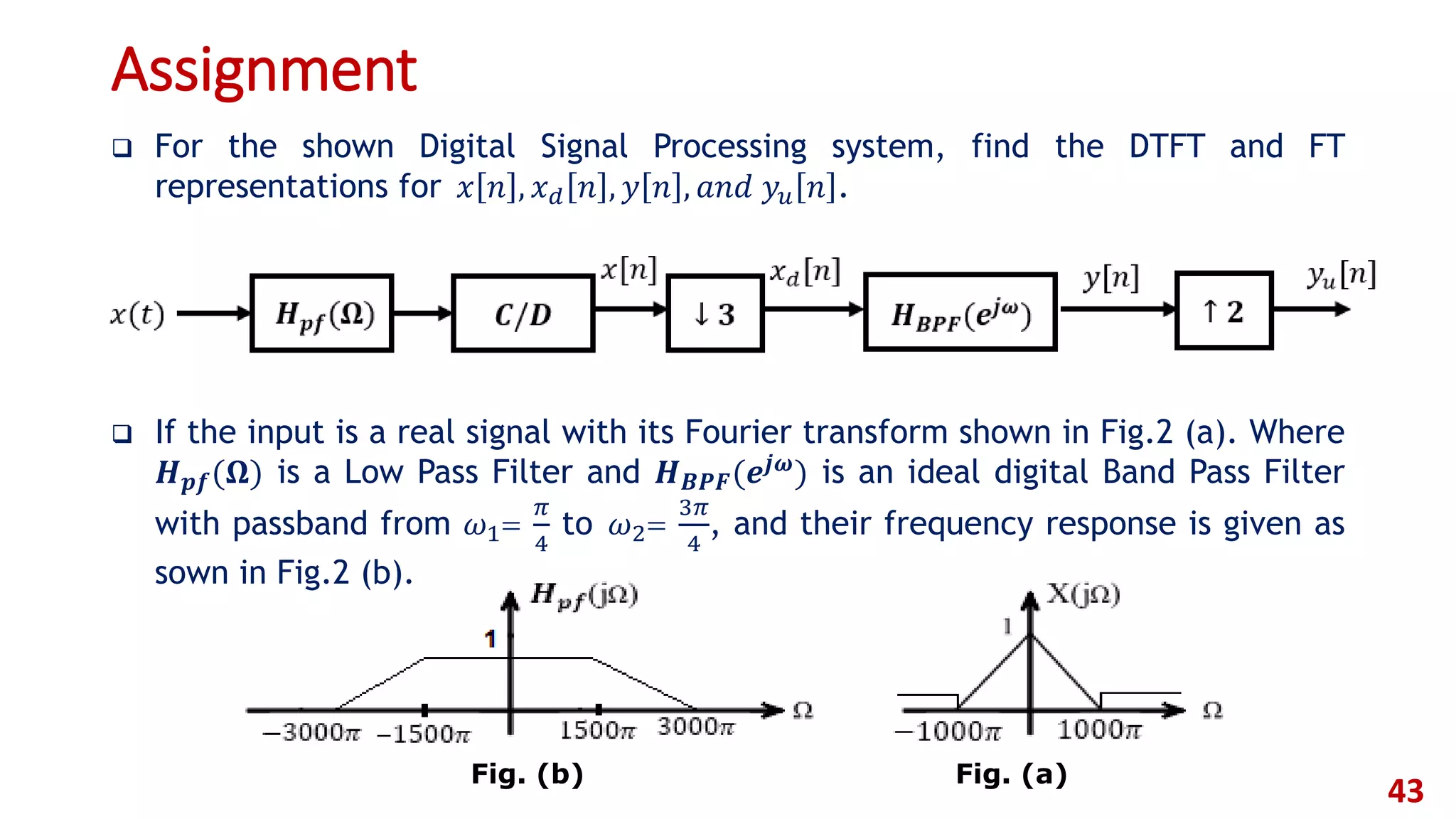
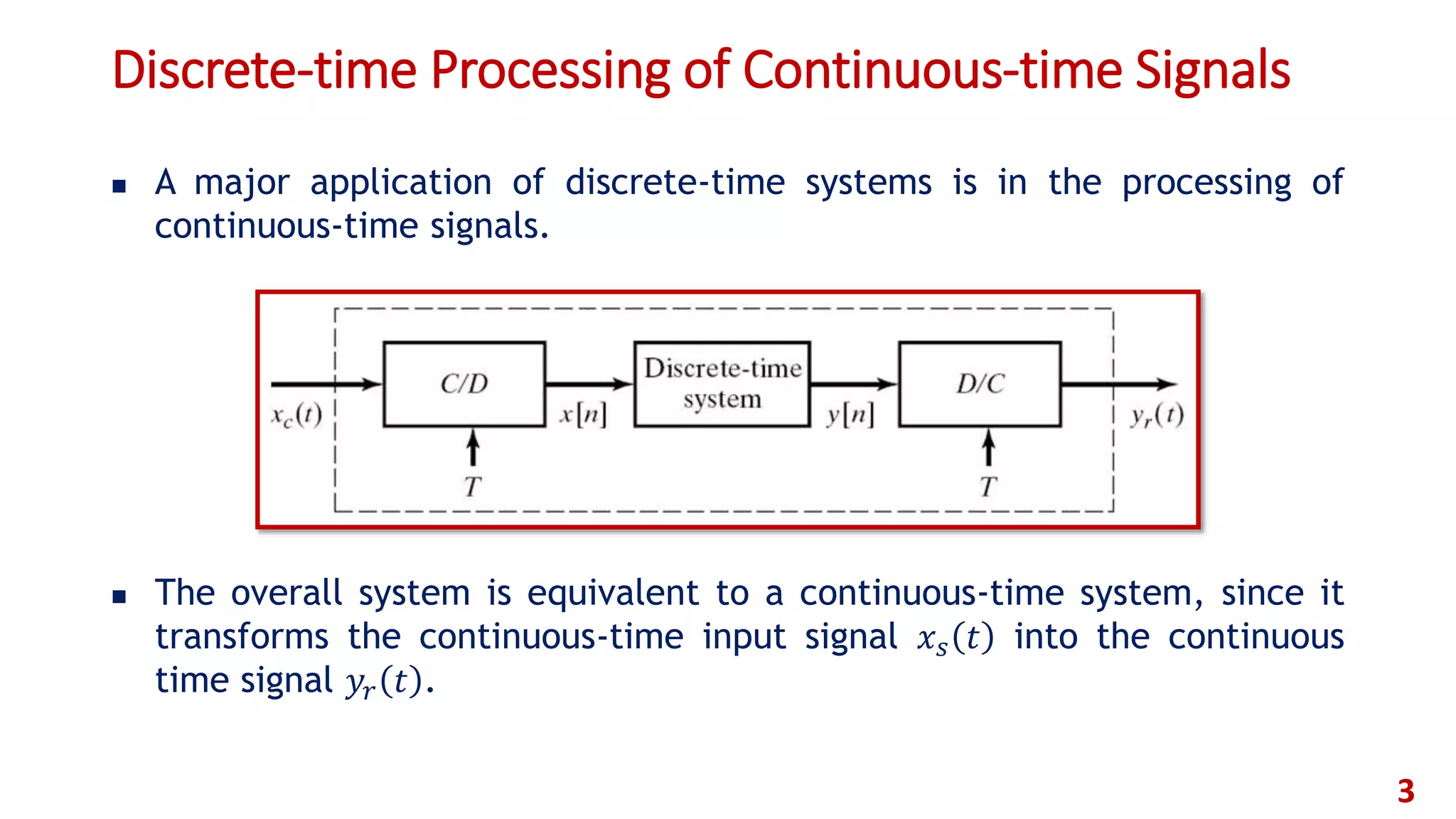
This document discusses multi-rate digital signal processing and concepts related to sampling continuous-time signals. It begins by introducing discrete-time processing of continuous signals using an ideal continuous-to-discrete converter. It then covers the Nyquist sampling theorem and relationships between continuous and discrete Fourier transforms. It discusses ideal and practical reconstruction using zero-order hold and anti-imaging filters. Finally, it introduces the concepts of downsampling and upsampling in multi-rate digital signal processing systems.

1. ‫ر‬َ‫ـد‬ْ‫ق‬‫ِـ‬‫ن‬،،،‫لما‬‫اننا‬ ‫نصدق‬ْْ‫ق‬ِ‫ن‬‫ر‬َ‫د‬
LECTURE (10)
Multi-Rate Digital Signal Processing
Assist. Prof. Amr E. Mohamed

2. Sampling Theorem
2

3. Discrete-time Processing of Continuous-time Signals
 A major application of discrete-time systems is in the processing of
continuous-time signals.
 The overall system is equivalent to a continuous-time system, since it
transforms the continuous-time input signal 𝑥 𝑠 𝑡 into the continuous
time signal 𝑦𝑟 𝑡 .
3

4. Continuous to discrete (Ideal C/D) converter
 The impulse train (sampling Signal) is
 Where
 The sampled signal in Time-domain (Time domain multiplication) is
4
   



n
cs nTttxtstxtx )()()(
   



n
nTtts      



n
snj
T
jS 
2
continuous
F. T.
Ts /2

5. Continuous to discrete (Ideal C/D) converter (Cont.)
 The sampled signal in Frequency-domain is
 Hence, the continuous Fourier transforms of 𝑥 𝑠(𝑡) consists of
periodically repeated copies of the Fourier transform of 𝑥 𝑐(𝑡).
 Review of Nyquist sampling theorem:
 Aliasing effect: If 𝛺 𝑠 < 2𝛺ℎ, the copies of 𝑋𝑐(𝑗𝛺) overlap, where 𝛺ℎ is the
highest nonzero frequency component of 𝑋𝑐(𝑗𝛺). 𝛺ℎ is referred to as the
Nyquist frequency.
5
)()(
2
1
)(  jSjXjX cs

    



n
scs njX
T
jX
1

6. C/D Converter
 Relationship between 𝑥(𝑡) and 𝑥 𝑛 is:
𝑥 𝑛 = 𝑥(𝑡) 𝑡=𝑛𝑇 = 𝑥 𝑛𝑇 , 𝑛 = ⋯ , −1, 0, 1, 2, 3, …
6

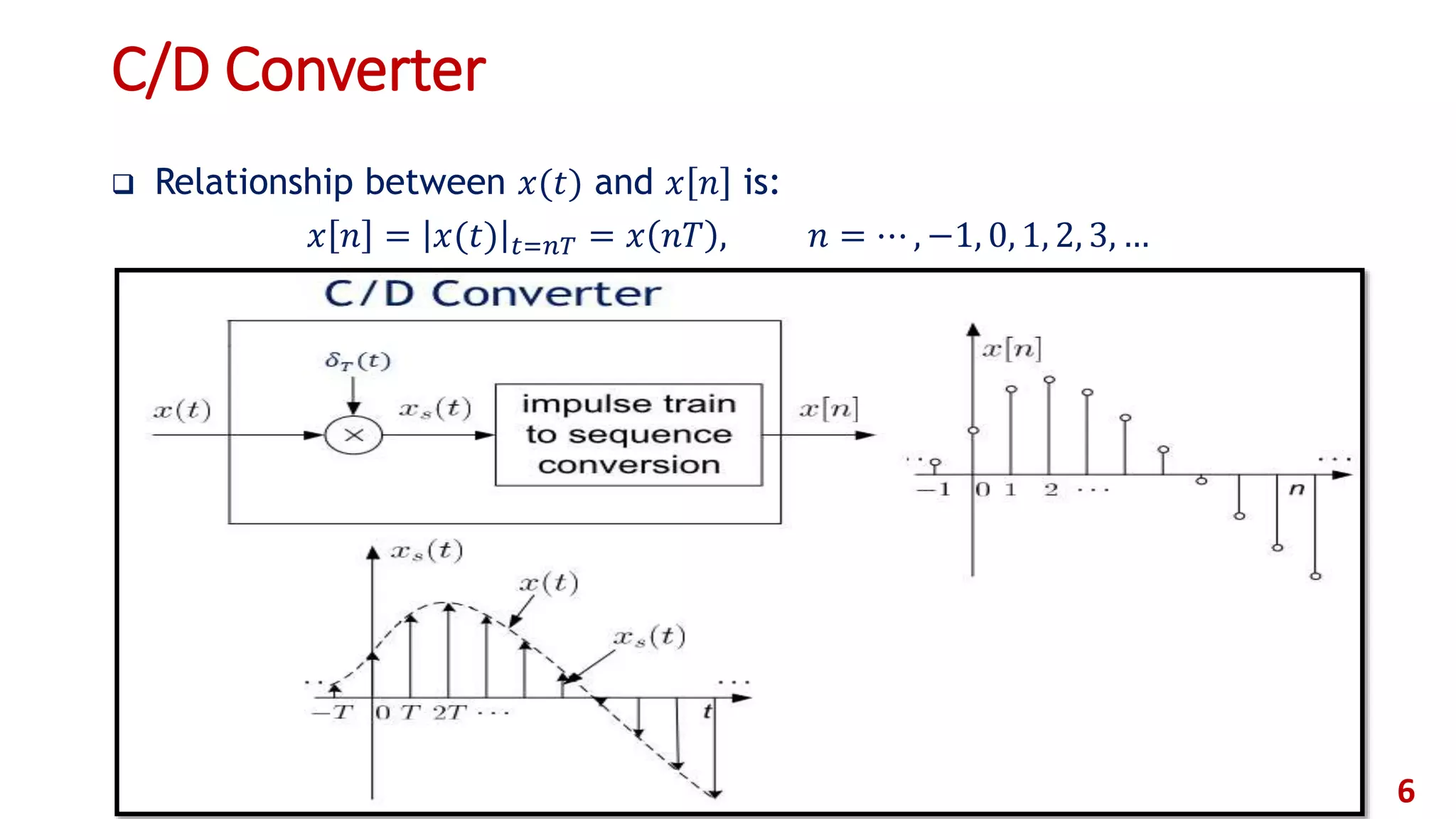
7. Continuous to discrete (Ideal C/D) converter (Cont.)
 In the above, we characterize the relationship of 𝑥 𝑠(𝑡) and 𝑥 𝑐(𝑡) in the
continuous F.T. domain.
 From another point of view, 𝑋𝑠(𝑗𝛺) can be represented as the linear
combination of a serious of complex exponentials:
 If 𝑥(𝑛𝑇) ≡ 𝑥[𝑛], its DTFT is
 The relation between digital frequency and analog frequency is 𝝎 = 𝛀𝐓 7
     



n
cs nTtnTxtx since
   




n
Tnj
cs enTxjX








n
nj
n
njj
enTxenxeX 
)(][)(

8. Continuous to discrete (Ideal C/D) converter (Cont.)
 Combining these properties, we have the relationship between the
continuous F.T. and DTFT of the sampled signal:
where
: represent continuous F.T.
: represent DTFT
 Thus, we have the input-output relationship of C/D converter
8
     

















n
s
c
n
sc
jw
T
n
T
jX
T
njX
T
eX
11
 jw
eX
 jXc
     Tj
T
j
s eXeXjX 





9. Discrete-to-continuous (Ideal D/C) converter
9

10. Ideal reconstruction filter
 The ideal reconstruction filter
is a continuous-time filter,
with the frequency response
being H 𝑟(𝑗𝛺) and impulse
response ℎ 𝑟(𝑡).
10
)/(
)/sin(
)(
Tt
Tt
thr




11. Combine C/D, discrete-time system, and D/C
 Consider again the discrete-time processing of continuous signals
 Let 𝐻(𝑒 𝑗𝜔) be the frequency response of the discrete-time system in
the above diagram. Since Y 𝑒 𝑗𝜔 = 𝐻 𝑒 𝑗𝜔 𝑋(𝑒 𝑗𝜔)
11

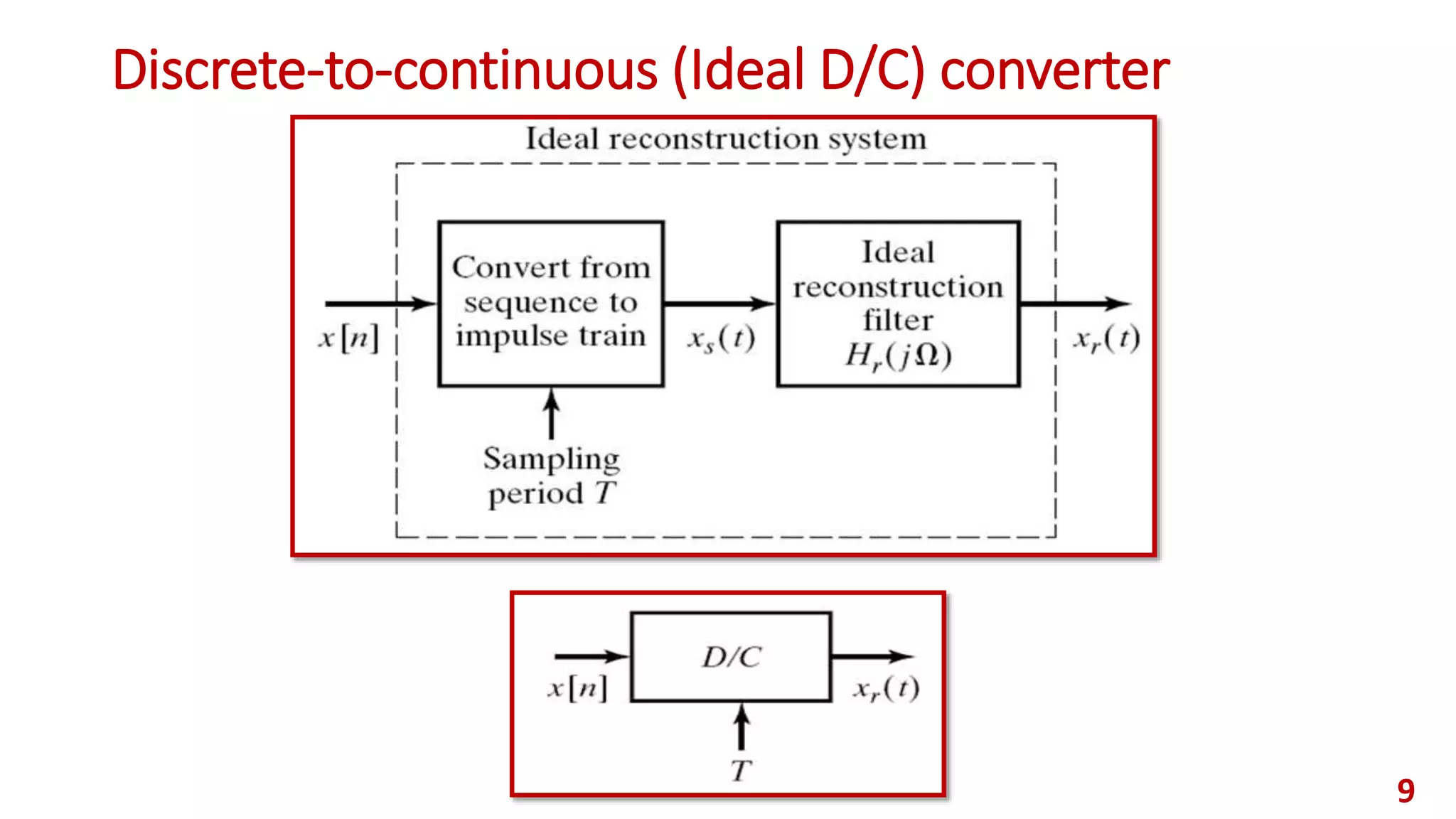
12. D/C converter revisited
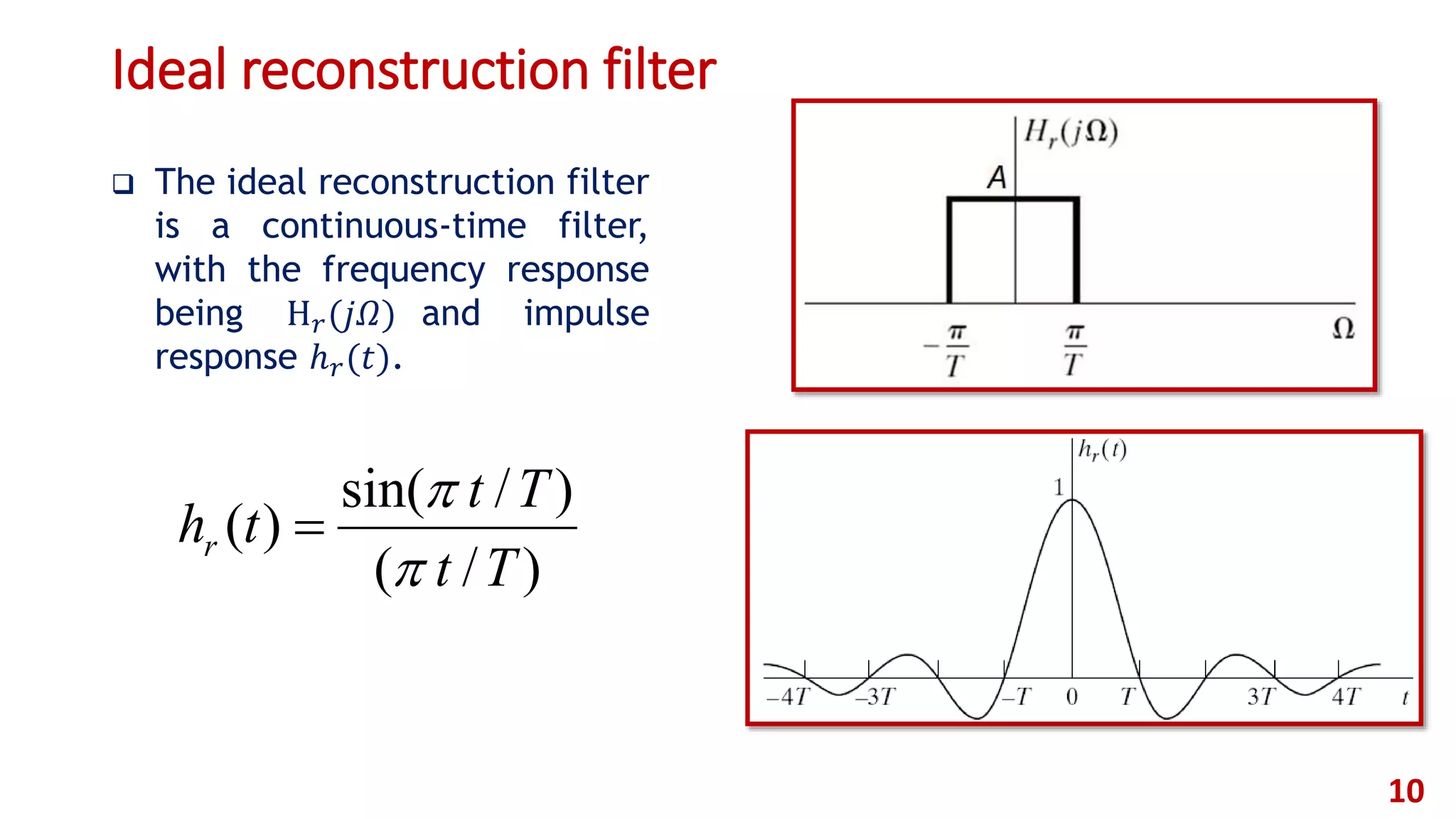
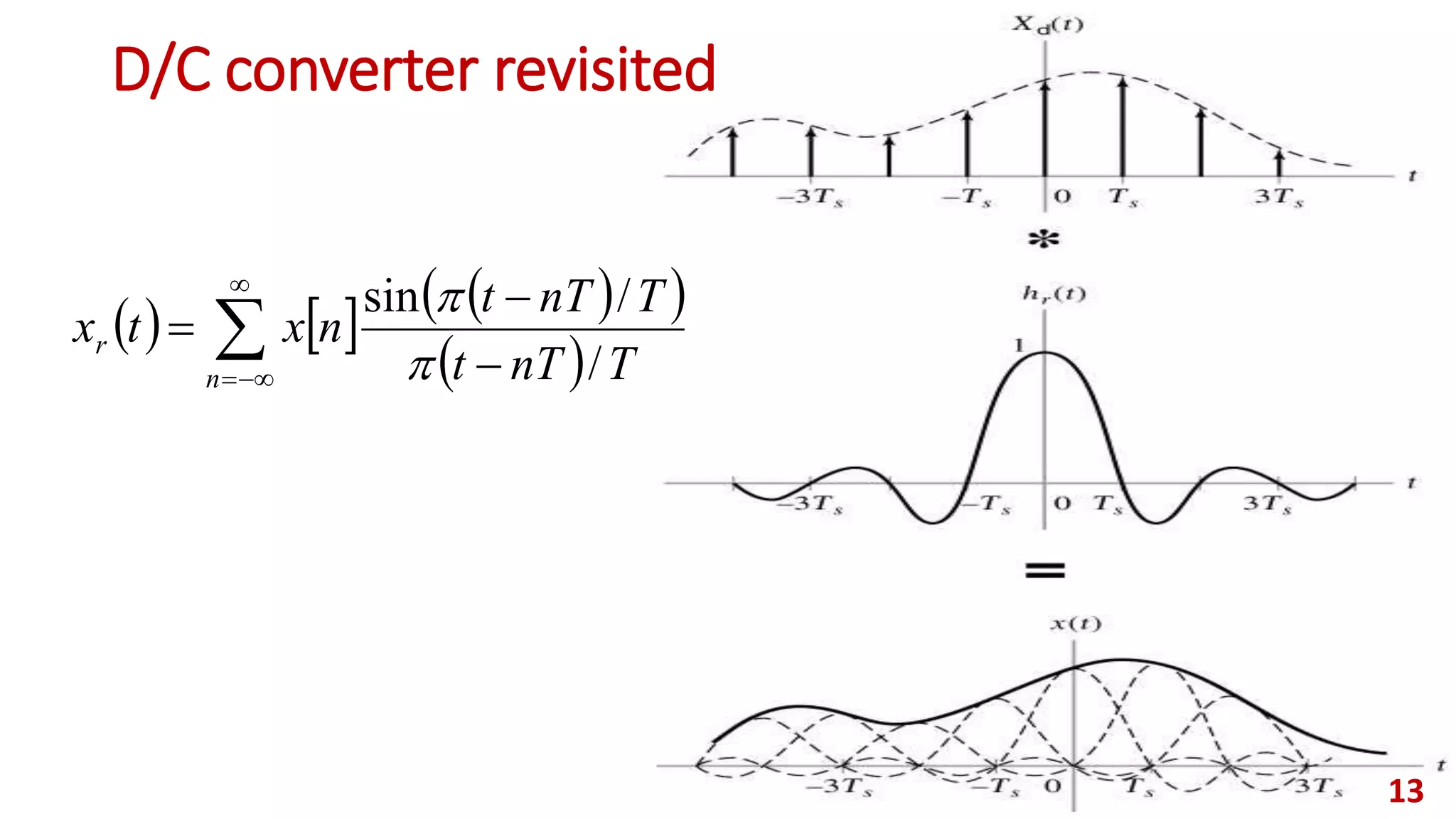
 An ideal low-pass filter 𝐻(𝑒 𝑗𝜔) that has a cut-off frequency Ω 𝑐 = Ω 𝑠/2
= 𝜋/𝑇 and gain 𝐴 is used for reconstructing the continuous signal.
 Frequency domain of D/C converter: [𝐻(𝑒 𝑗𝜔) is its frequency response]
 Remember that the corresponding impulse response is a 𝑠𝑖𝑛𝑐 function, and
the reconstructed signal is
12
      
 

 


n
r
TnTt
TnTt
nyty
/
/sin


       


 



otherwise
TeYA
eYjHjY
Tj
Tj
rr
,0
/, 

13. D/C converter revisited
13
      
 

 


n
r
TnTt
TnTt
nxtx
/
/sin



14. Practical Reconstruction
 We cannot build an ideal Low-Pass-Filter.
 Practical systems could use a zero-order hold block
 This distorts signal spectrum, and compensation is needed
14

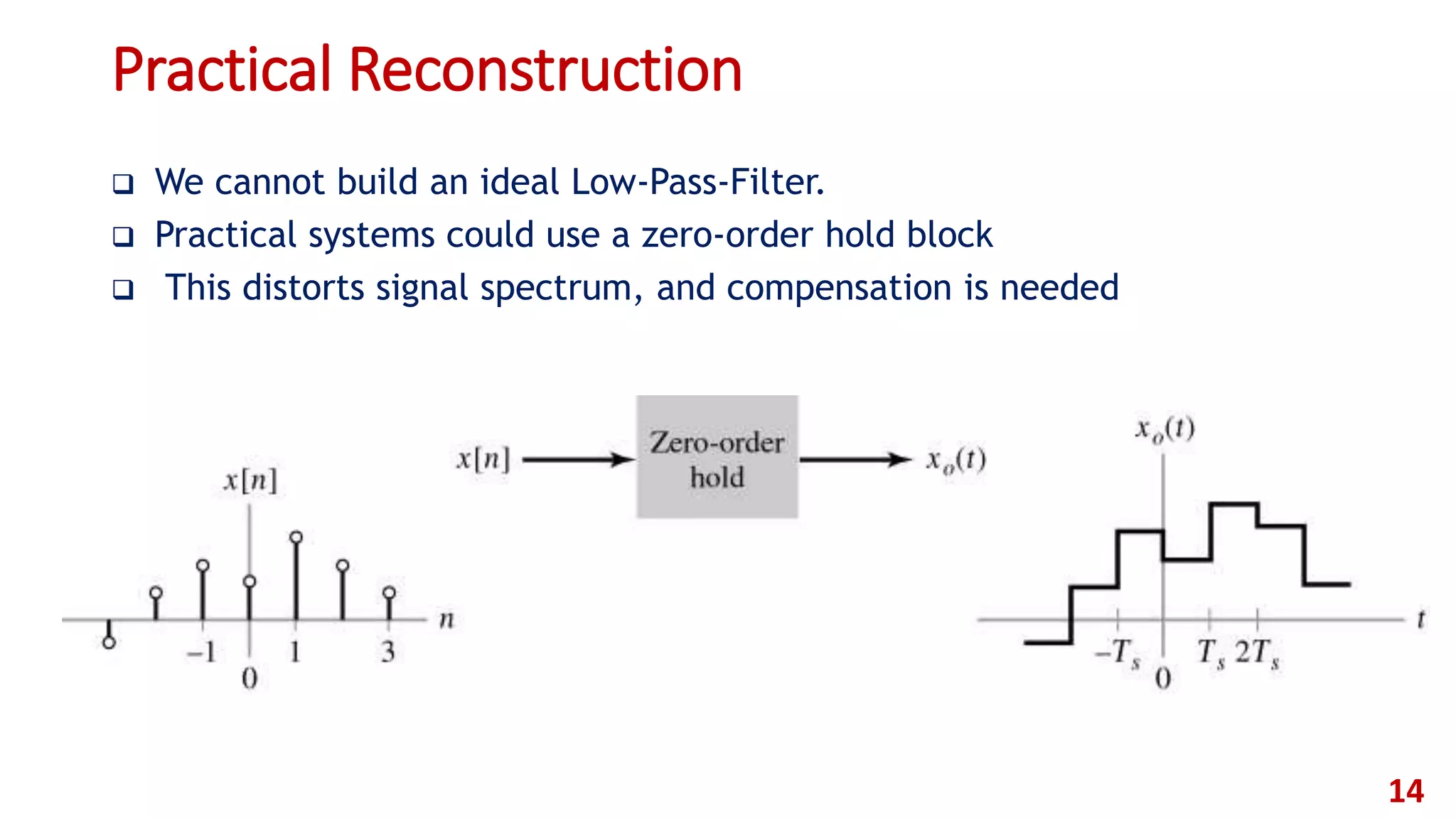
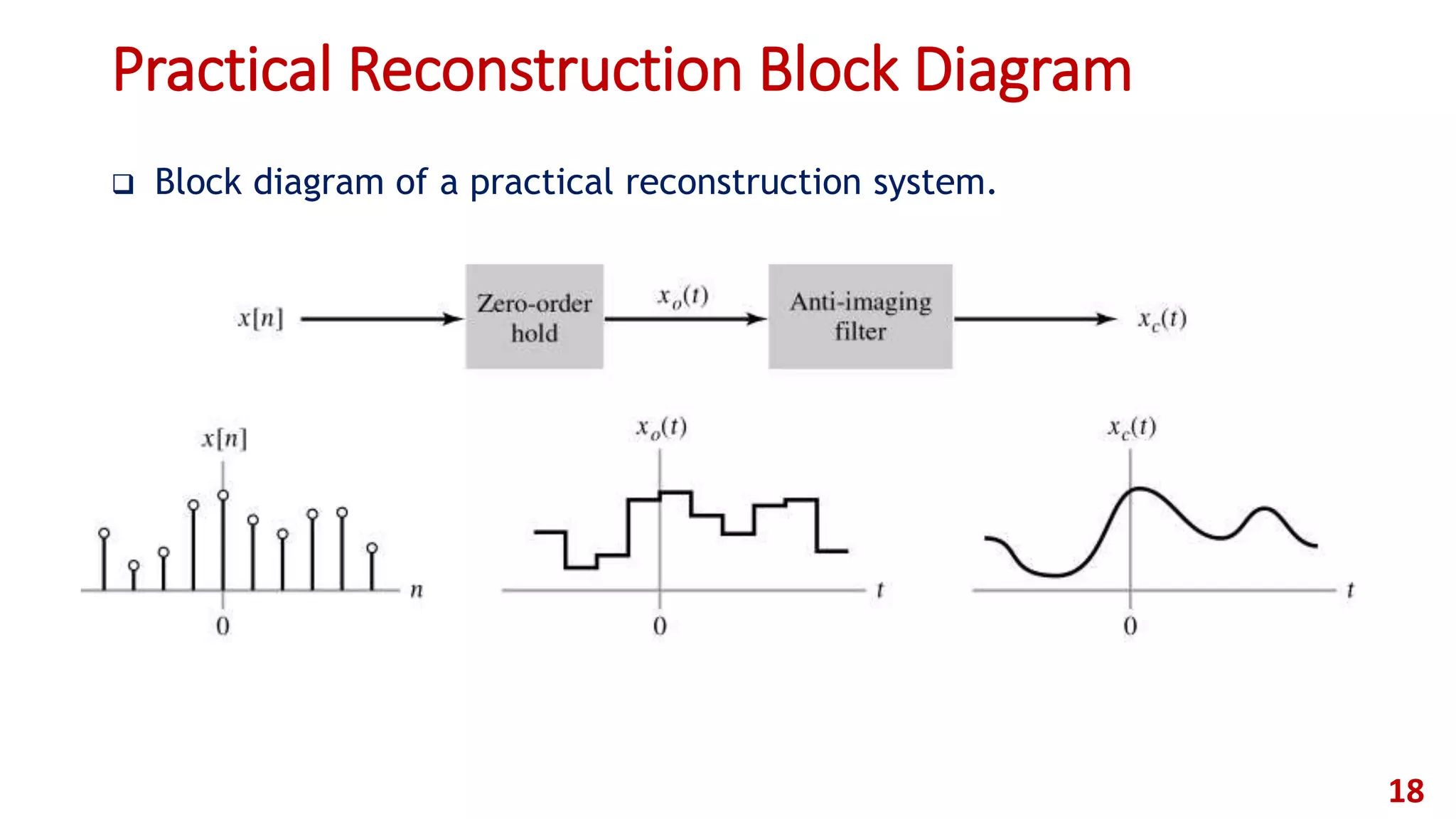
15. Practical Reconstruction (Zero-Order Hold)
 Rectangular pulse used to analyze zero-order hold reconstruction
15






s
s
Ttt
Tt
th
,0,0
0,1
)(0









n
s
n
s
nTthnx
nTtnxth
thtxtx
)(][
)(][)(
)()()(
0
0
00






 )2/sin(
2)(
)()()(
2/
0
00
sTj T
ejH
jXjHjX
s


16. Practical Reconstruction
(Zero-Order Hold)
 Effect of the zero-order hold in the
frequency domain.
a) Spectrum of original continuous-time
signal.
b) spectrum of sampled signal.
c) Magnitude of Ho(j).
d) Phase of Ho(j).
e) Magnitude spectrum of signal
reconstructed using zero-order hold.
16

17. Practical Reconstruction (Anti-imaging Filter)
 Frequency response of a compensation filter used to eliminate some of
the distortion introduced by the zero-order hold.
17









ms
m
s
s
c T
T
jH


||,0
||,
)2/sin(2)(
Anti-imaging filter.

18. Practical Reconstruction Block Diagram
 Block diagram of a practical reconstruction system.
18

19. Analog Processing using DSP
 Block diagram for discrete-time processing of continuous-time signals.
19
(b) Equivalent continuous-time system.
(a) A basic system.

20. Idea: find the CT system
 0th-order S/H:
20
)()()(such that)()(  jXjGjYjGtg FT



  )2/sin(
2)( 2/
0
sTj T
ejH s

)()()(  jXjHjX aa 
 
 















n
ssa
Tj
c
s
n
ssa
Tj
s
ss
n
ssa
s
n
sa
s
kjXkjHeHjHjH
T
jY
kjXkjHeH
T
jY
TkjXkjH
T
kjX
T
jX
s
s
))(())(()()(
1
)(
))(())((
1
)(
/2,))(())((
1
))((
1
)(
0 








21. Idea: find the CT system (Cont.)
 If no aliasing, the anti-imaging filter Hc(jw) eliminates frequency
components above s/2, leaving only k=0 terms
 If anti-aliasing and anti-imaging filters are chosen to compensate the
effects of sampling and reconstruction, then
21
 
  )()()(
1
)(
)()()()(
1
)(
0
0




jHeHjHjH
T
jG
jXjHeHjHjH
T
jY
a
Tj
c
s
a
Tj
c
s
s
s


 sTj
acs
eHjG
jHjHjHT





)(Thus,
1)()()()/1( 0

22. Multi-Rate Digital Signal Processing
Downsampling (Decimation) and Upsampling (Interpolation)
22

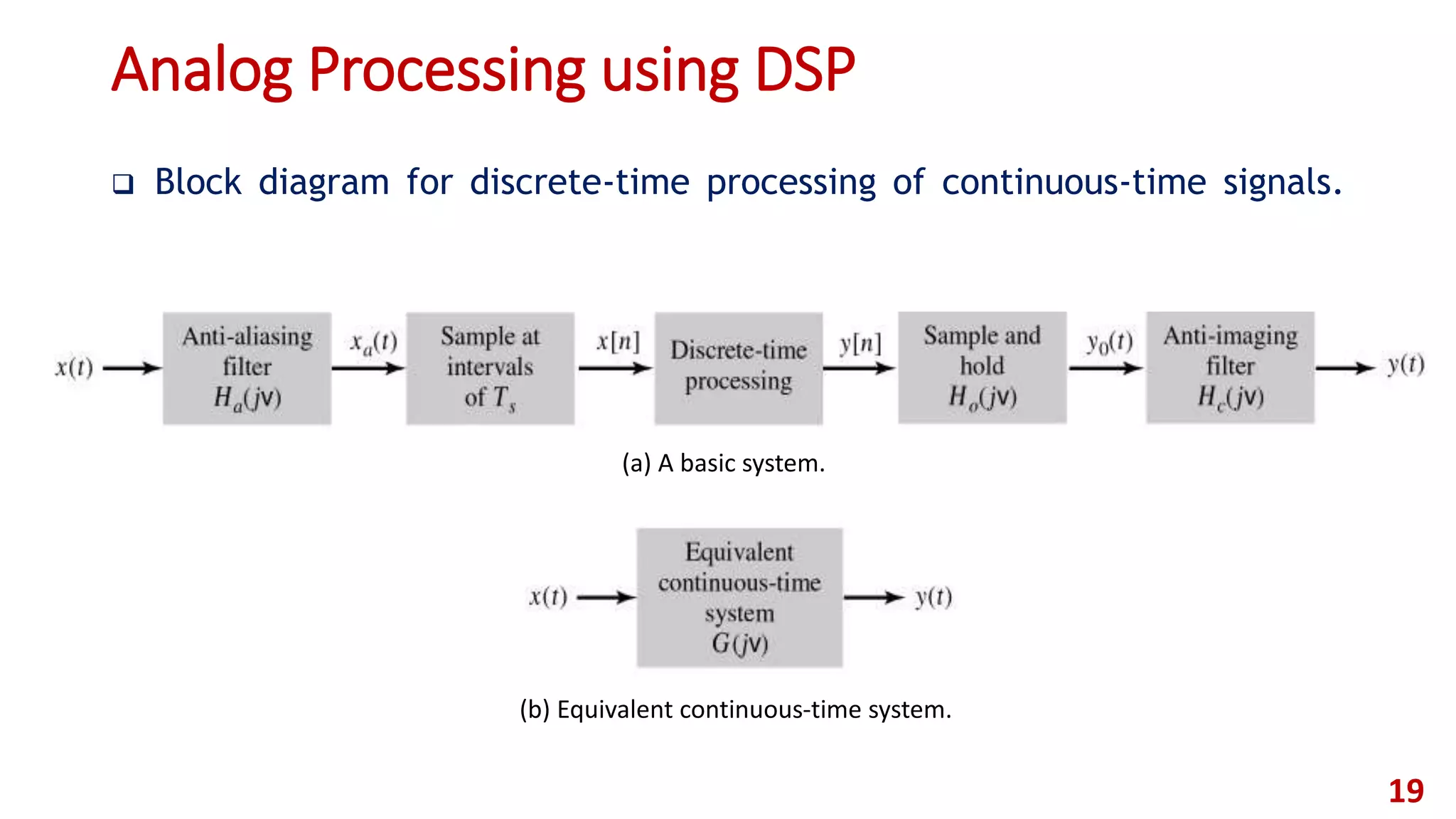
23. Digital Signal Processing
 Provided that :
𝐻 𝑎 𝑗Ω =
1 Ω ≤
Ω 𝑠
2
0 Ω >
Ω 𝑠
2
𝐺 𝑒𝑓𝑓 𝑗Ω =
𝐻 𝑎 𝑗Ω 𝐺 𝑒 𝑗Ω𝑇
𝐻 𝑜 𝑗Ω 𝐻𝑟 𝑗Ω Ω ≤
Ω 𝑠
2
0 Ω >
Ω 𝑠
2 23
Digital Signal
Processor
C/D
Sample
nT
𝑥(𝑡)
𝑋(𝑗Ω)
Antialiasing
Analog
Filter
𝑯 𝒂(𝒋𝛀)
𝑥 𝑎(𝑡)
𝑋 𝑎(𝑗Ω)
𝑥[𝑛]
𝑋(𝑒 𝑗𝜔
)
Reconstruction
Analog
Filter
𝑯 𝒓(𝒋𝛀)
𝑮(𝒆𝒋𝝎)
𝑦[𝑛]
𝑌(𝑒 𝑗𝜔
)
𝑦𝑎(𝑡)
𝑌𝑎(𝑗Ω)𝑯 𝒐(𝒋𝛀)
D/C
Zero order
hold
𝑦(𝑡)
𝑌(𝑗Ω)
𝑮 𝒆𝒇𝒇(𝒋𝛀)
𝑦(𝑡)
𝑌(𝑗Ω)𝑋(𝑗Ω)
𝑥(𝑡)

24. Introduction
 In single-rate DSP systems, all data is sampled at the same rate no
change of rate within the system.
 In Multirate DSP systems, sample rates are changed (or are different)
within the system
 Multirate can offer several advantages
 reduced computational complexity
 reduced transmission data rate.
24

25. Example: Audio sample rate conversion
 Recording studios use 192 kHz
 CD uses 44.1 kHz
 wideband speech coding using 16 kHz
 Master from studio must be rate-converted by a factor 44.1/192
25

26. Example: Oversampling ADC
 Consider a Nyquist rate ADC in which the signal is sampled at the
desired precision and at a rate such that Nyquist’s sampling criterion is
just satisfied.
 Bandwidth for audio is 20 Hz < f < 20 kHz
 The required Antialiasing filter has very demanding specification
 Requires high order analogue filter such as elliptic filters that have very
nonlinear phase characteristics
• hard to design, expensive and bad for audio quality.
26

27.  Nyquist Rate Conversion Anti-aliasing Filter.
 Building a narrow band filters 𝐻 𝑎(𝑗Ω) and 𝐻 𝑜(𝑗Ω) is difficult &
expensive.
27

28.  Consider oversampling the signal at, say, 64 times the Nyquist rate but
with lower precision. Then use multirate techniques to convert sample
rate back to 44.1 kHz with full precision.
 New (over-sampled) sampling rate is 44.1 × 64 kHz.
 Requires simple antialiasing filter
 Could be implemented by simple filter (eg. RC network)
 Recover desired sampling rate by downsampling process.
28

29.  Oversampled Conversion Antialiasing Filter
29

30. Multirate Digital Signal Processing
 The solution is changing sampling rate using downsampling and
upsampling.
 Low cos:
 Analog filter (eg. RC circuit)
 Storage / Computation
 Price:
 Extra Computation for ↓ 𝑴 𝟏 and ↑ 𝑴 𝟐
 Faster ADC and DAC
30
DSPC/D
Sample
nT
𝑥(𝑡)
𝑋(𝑗Ω)
Antialiasing
Analog
Filter
𝑯 𝒂(𝒋𝛀)
𝑥 𝑎(𝑡) 𝑥[𝑛]
Reconstruction
Analog
Filter
𝑯 𝒓(𝒋𝛀)
𝑮(𝒆𝒋𝝎
)
𝑦[𝑛] 𝑦𝑎(𝑡)
𝑯 𝒐(𝒋𝛀)
D/C
Zero order
hold 𝑦(𝑡)
𝑌(𝑗Ω)
↓ 𝑴 𝟏
Downsampler
𝑥1[𝑛]
↑ 𝑴 𝟐
Upsampler
𝑦2[𝑛]

31. Example (1)
 Given a 2nd order analog filter
 Evaluate 𝐻 𝑎 𝑗Ω for
 Anti-aliasing filter
 Zero-Order-Hold
 Anti-imaging filter
 At sampling frequency:
 Sampling frequency = 300Hz.
 Sampling frequency = 2400Hz. (8x Oversampling)
31
𝐻 𝑎 𝑗Ω =
(200𝜋)2
(𝑗Ω + 200𝜋)2
, 𝑠𝑖𝑔𝑛𝑎𝑙 𝐵𝑊 − 50 < 𝑓 < 50

32. Example (1): Ideal Anti-aliasing Filter
 The required specification is
𝐻 𝑎 𝑗Ω =
1 Ω ≤ 100𝜋
0 Ω > 100𝜋
 In case of Ω 𝑠 = 600𝜋
 In case of Ω 𝑠 = 4800𝜋
 Passband constraint same for both cases
 𝐻 𝑎 𝑗100𝜋 =
(200𝜋)2
200𝜋(𝑗
1
2
+1)
2 =
4
5
= 0.8
 Stopband actual
 𝐻 𝑎 𝑗500𝜋 =
(200𝜋)2
200𝜋(𝑗
5
2
+1)
2 =
4
29
≅ 0.14
 𝐻 𝑎 𝑗4700𝜋 =
(200𝜋)2
200𝜋(𝑗
47
2
+1)
2 =
4
472+4
≅ 0.002
32
76𝑋 𝑎𝑡𝑡𝑒𝑛𝑢𝑎𝑡𝑖𝑜𝑛 𝑜𝑓 1

33. Example (1): Ideal Anti-imaging Filter
 The required specifications are shown in the figure
 In case of Ω 𝑠 = 600𝜋,
 Desired at Ω = 100𝜋
• 𝐻𝑟 𝑗100𝜋 =
𝜋/6
𝑠𝑖𝑛 𝜋/6
≅ 1.06
 Actual filter at
• Passband: 𝐻 𝑎 𝑗100𝜋 =
(200𝜋)2
200𝜋(𝑗
1
2
+1)
2 =
4
5
= 0.8
• Stopband: 𝐻 𝑎 𝑗500𝜋 =
(200𝜋)2
200𝜋(𝑗
5
2
+1)
2 =
4
29
≅ 0.14
 In case of Ω 𝑠 = 4800𝜋
 Desired at Ω = 100𝜋
• 𝐻𝑟 𝑗100𝜋 =
𝜋/48
𝑠𝑖𝑛 𝜋/48
≅ 1.007
 Actual filter at
• Passband: 𝐻 𝑎 𝑗100𝜋 =
(200𝜋)2
200𝜋(𝑗
1
2
+1)
2 =
4
5
= 0.8
• Stopband: 𝐻 𝑎 𝑗500𝜋 =
(200𝜋)2
200𝜋(𝑗
5
2
+1)
2 =
4
29
≅ 0.002
33
 
)/sin(
/
)2/sin(2 s
s
s
s
r
T
T
jH









34. Downsampling (Decimation ):
 To relax design of anti-aliasing filter and anti-imaging filters, we wish to
use high sampling rates.
 High-sampling rates lead to expensive digital processor
 Wish to have:
• High rate for sampling/reconstruction
• Low rate for discrete-time processing
 This can be achieved using downsampling/upsampling
34

35. Downsampling
 Let 𝑥1 𝑛 and 𝑥2 𝑛 be obtained by sample 𝑥(𝑡) with sampling interval 𝑇 and MT,
respectively.
35
𝑥 𝑎(𝑡)
𝑋 𝑎(𝑗Ω) 𝑋1(𝑒 𝑗𝜔)
𝑥1[n]A/D
Sample @T
Ω 𝑠
𝑥 𝑎(𝑡)
𝑋 𝑎(𝑗Ω) 𝑋2(𝑒 𝑗𝜔
)
𝑥2[n]A/D
Sample @MT
Ω 𝑠/𝑀
T
MT
𝟐𝝅 𝟒𝝅𝟐𝝅𝟒𝝅 T𝛀 𝒐T𝛀 𝒐
𝟐𝝅 𝟒𝝅𝟐𝝅𝟒𝝅

36. Downsampling Block
𝑥[n]
𝑋(𝑒 𝑗𝜔
)
Discrete Time
Low-Pass Filter
𝐻 𝑑(𝑒 𝑗𝜔
)
𝑤[n]
𝑊(𝑒 𝑗𝜔
) 𝑌(𝑒 𝑗𝜔
)
𝑦 n = 𝑤[Mn]Discard Values
𝑛 ≠ 𝑀𝑙
𝝅
𝑴
𝝅
𝝅
𝑴
(d) Spectrum after Downsampling.
(c) Spectrum of filter output.
(b) Filter frequency response.
(a) Spectrum of oversampled input signal.
Noise is depicted as the shaded portions
of the spectrum.
𝑌(𝑒 𝑗𝜔)
𝑦 nDownsampler
↓ 𝑀
𝑥[n]
𝑋(𝑒 𝑗𝜔)

37. Downsampling Block
 Note: if 𝑦 n = 𝑤[Mn], then
𝑌 𝑒 𝑗𝜔 =
1
𝑀
𝑚=0
𝑀−1
𝑋 𝑒 𝑗(𝜔−2𝜋𝑚)/𝑀
 What does 𝑌 𝑒 𝑗𝜔
=
1
𝑀 𝑚=0
𝑀−1
𝑋 𝑒 𝑗(𝜔−2𝜋𝑚)/𝑀
represent?
 Stretching of 𝑋(𝑒 𝑗𝜔) to 𝑋(𝑒 𝑗𝜔/𝑀)
 Creating M − 1 copies of the stretched versions
 Shifting each copy by successive multiples of 2𝜋 and superimposing (adding)
all the shifted copies
 Dividing the result by M
37
Discrete Time
Low-Pass Filter
𝐻 𝑑(𝑒 𝑗𝜔
)
𝑤[n]
𝑊(𝑒 𝑗𝜔) 𝑌(𝑒 𝑗𝜔
)
𝑦 n = 𝑤[Mn]Discard Values
𝑛 ≠ 𝑀𝑙

38. Upsampling
 Let 𝑥1 𝑛 and 𝑥2 𝑛 be obtained by sample 𝑥(𝑡) with sampling interval 𝑇 and T/M,
respectively.
38
𝑥 𝑎(𝑡)
𝑋 𝑎(𝑗Ω) 𝑋1(𝑒 𝑗𝜔)
𝑥1[n]A/D
Sample @T
Ω 𝑠
𝑥 𝑎(𝑡)
𝑋 𝑎(𝑗Ω) 𝑋2(𝑒 𝑗𝜔
)
𝑥2[n]A/D
Sample @T/M
𝑀 Ω 𝑠
M
T

T
𝟐𝝅 𝟒𝝅𝟐𝝅𝟒𝝅
𝟐𝝅 𝟒𝝅𝟐𝝅𝟒𝝅

39. Upsampling (zero padding) Block Diagram
39
Insert (M-1) zeros
between each two
successive samples
𝑥2[n]
𝑋2(𝑒 𝑗𝜔
)
Discrete Time
Low-Pass Filter
𝐻𝑖(𝑒 𝑗𝜔
)
𝑋𝑖(𝑒 𝑗𝜔
)
𝑥𝑖 nUpsampler
↑ 𝑀
𝑥[n]
𝑋(𝑒 𝑗𝜔
)

40. Upsampling (zero padding) Block Diagram
𝑥2 𝑛 =
𝑥[
𝑛
𝑀
]
𝑛
𝑀
𝑖𝑛𝑡𝑒𝑔𝑒𝑟
0 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒
 or
𝑥2 𝑛 =
𝑘=−∞
∞
𝑥 𝑘 𝛿(𝑛 − 𝑘𝑀)
 The frequency spectrum is
𝑋2(𝑒 𝑗𝜔
) =
𝑛=−∞
∞
𝑘=−∞
∞
𝑥 𝑘 𝛿(𝑛 − 𝑘𝑀) 𝑒−𝑗𝑛𝜔
𝑋2(𝑒 𝑗𝜔
) =
𝑘=−∞
∞
𝑥 𝑘
𝑛=−∞
∞
𝛿(𝑛 − 𝑘𝑀) 𝑒−𝑗𝑛𝜔
𝑋2 𝑒 𝑗𝜔 =
𝑘=−∞
∞
𝑥 𝑘 𝑒−𝑗𝑘𝑀𝜔 = 𝑋 𝑒 𝑗𝑀𝜔 = 𝑋 𝑒 𝑗 𝜔 , 𝑤ℎ𝑒𝑟𝑒 𝜔 = 𝑀𝜔
40

41. Upsampling (zero padding) Block Diagram
41
𝑥[n]
𝑋(𝑒 𝑗𝜔
)
Insert (M-1) zeros
between each two
successive samples
𝑥2[n]
𝑋2(𝑒 𝑗𝜔
) 𝑋𝑖(𝑒 𝑗𝜔
)
𝑥𝑖 nDiscrete Time
Low-Pass Filter
𝐻𝑖(𝑒 𝑗𝜔
) 𝑋𝑖(𝑒 𝑗𝜔)
𝑥𝑖 nUpsampler
↑ 𝑀
𝑥[n]
𝑋(𝑒 𝑗𝜔
)
(a) Spectrum of original sequence.
(b) Spectrum after inserting (M – 1) zeros in
between every value of the original sequence.
(c) Frequency response of a filter for removing
undesired replicates located at  2/M,  4/M, …, 
(M – 1)2/M.
(d) Spectrum of interpolated sequence.
𝝅

42. Continuous Signal Processing Using DSP
 Block diagram of a system for discrete-time processing of continuous-
time signals including decimation and interpolation.
42

43. Assignment
 For the shown Digital Signal Processing system, find the DTFT and FT
representations for 𝑥 𝑛 , 𝑥 𝑑 𝑛 , 𝑦 𝑛 , 𝑎𝑛𝑑 𝑦𝑢 𝑛 .
 If the input is a real signal with its Fourier transform shown in Fig.2 (a). Where
𝑯 𝒑𝒇(𝛀) is a Low Pass Filter and 𝑯 𝑩𝑷𝑭(𝒆𝒋𝝎) is an ideal digital Band Pass Filter
with passband from 𝜔1
𝜋
4
to 𝜔2
3𝜋
4
, and their frequency response is given as
sown in Fig.2 (b).
43
Fig. (b) Fig. (a)

44. 44