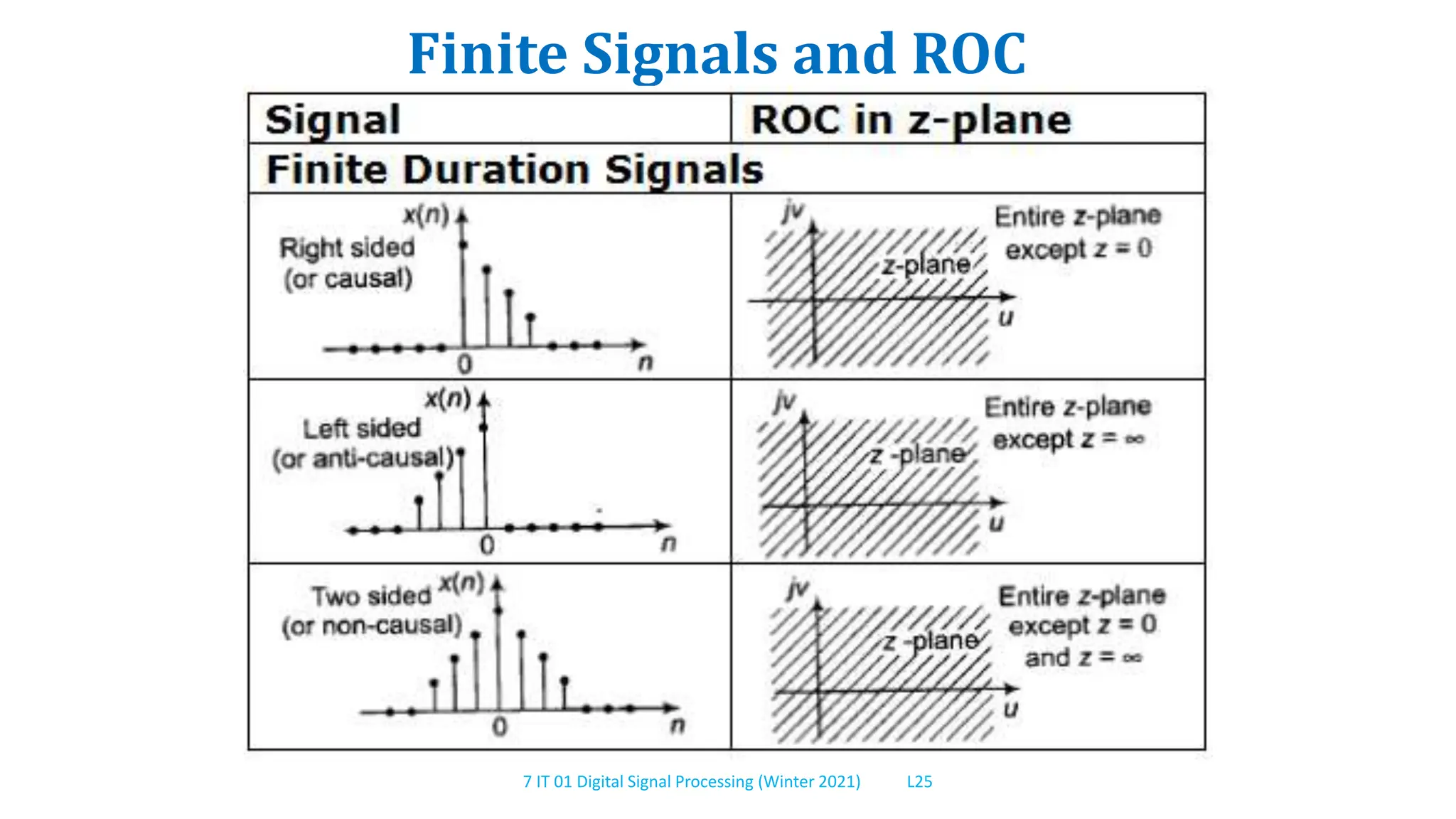
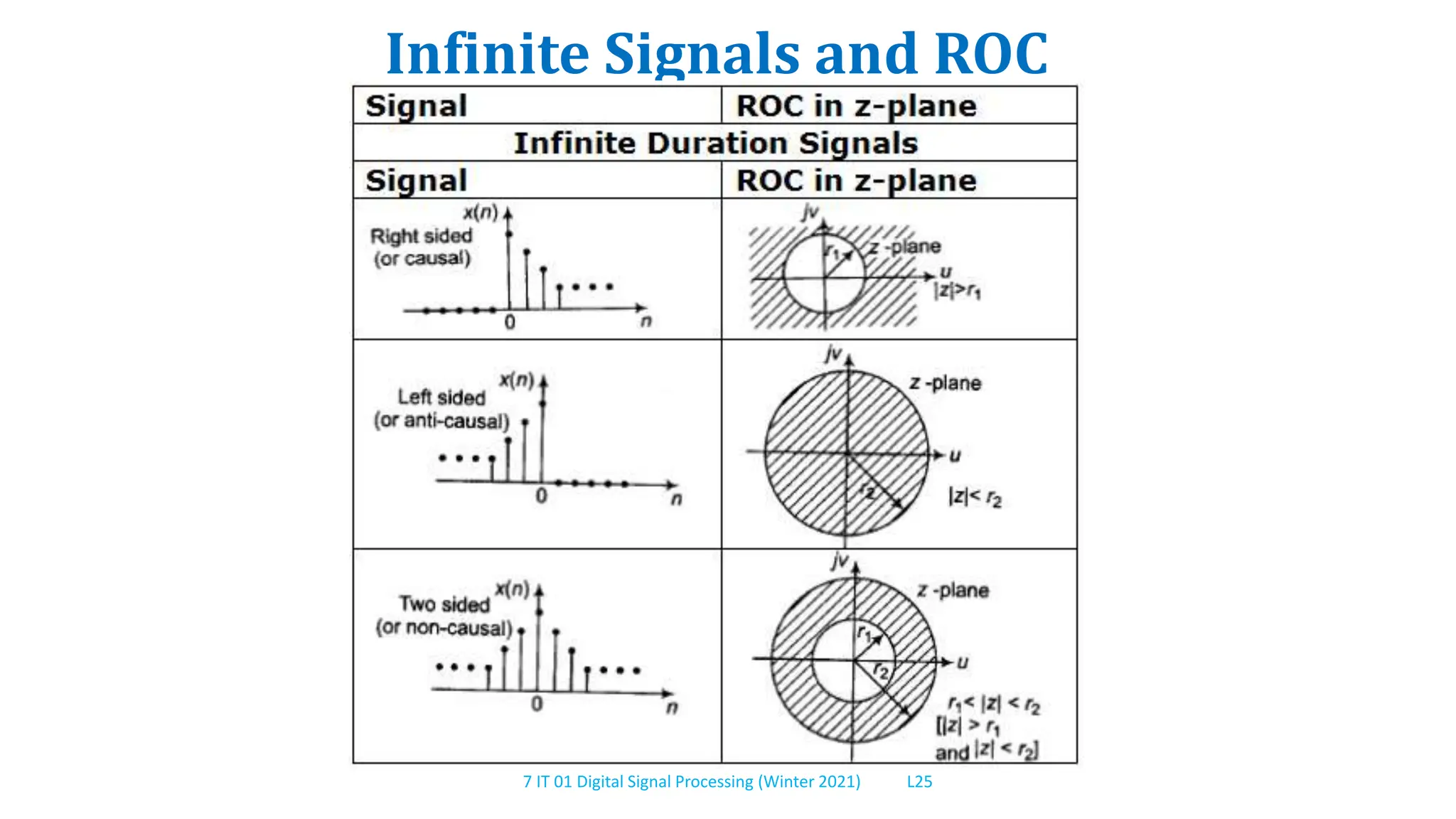
This document provides an overview of frequency analysis using the Z-transform. It defines the Z-transform, discusses its properties and relationship to the Fourier transform. Examples are provided to demonstrate calculating the Z-transform of different signals and determining the region of convergence. Key topics covered include the definition of the Z-transform, its region of convergence, properties, inverse Z-transform, and analyzing discrete time linear time-invariant systems using the Z-transform.





































![7 IT 01 Digital Signal Processing (Winter 2021) L25
Problems on Linearity Property
EX: Determine the z transform of signal 𝑥(𝑛) = (cos 𝑤0𝑛)u(n)
Solution : Given signal is 𝑥(𝑛) = (cos 𝑤0𝑛)u(n)
This signal can be decomposed by using Eular’s Identity as
cos 𝑤0𝑛 =
𝑒𝑗𝑤0𝑛 + 𝑒−𝑗𝑤0𝑛
2
So 𝑥(𝑛) = (
𝑒𝑗𝑤0𝑛+𝑒−𝑗𝑤0𝑛
2
)u(n)
Thus the decomposed signal is represented as
𝑥 𝑛 =
𝑒𝑗𝑤0𝑛
2
u n +
𝑒−𝑗𝑤0𝑛
2
u n
𝑋 𝑧 =
1
2
[𝑧(𝑒𝑗𝑤0𝑛)+𝑧(𝑒−𝑗𝑤0𝑛)]
We can write 𝑥1(𝑛) = 𝑒𝑗𝑤0𝑛𝑢(𝑛) and 𝑥2(𝑛) = 𝑒−𝑗𝑤0𝑛𝑢(𝑛)](https://image.slidesharecdn.com/3dspunitiiisession2021-22-240108114546-f1ee9436/75/Frequency-Analysis-using-Z-Transform-pptx-40-2048.jpg)
![7 IT 01 Digital Signal Processing (Winter 2021) L25
Problems on Linearity Property
𝑿 𝒛 =
𝟏
𝟐
[𝒛(𝒆𝒋𝒘𝟎𝒏)+𝒛(𝒆−𝒋𝒘𝟎𝒏)]
We can write 𝑥1 = 𝑒𝑗𝑤0𝑛𝑢(𝑛) and 𝑥2 = 𝑒−𝑗𝑤0𝑛𝑢(𝑛)
Let us say 𝛼 = 𝑒𝑗𝑤0 so 𝛼 = 𝑒𝑗𝑤0 = 1
𝑋1 𝑧 = 𝑧{ 𝑒𝑗𝑤0𝑛 𝑢 𝑛 } = 𝑛=0
∞
𝑒𝑗𝑤0𝑛 𝑧−𝑛
𝑋1 𝑧 = 𝑛=0
∞
(𝑒𝑗𝑤0𝑧−1)𝑛 =
1
1−(𝑒𝑗𝑤0𝑧−1)
where |𝑒𝑗𝑤0𝑧−1| < 1
As 𝑒𝑗𝑤0 = 1 , ROC is |z|> 1
Now let us say 𝛼 = 𝑒−𝑗𝑤0 so 𝛼 = 𝑒−𝑗𝑤0 = 1
𝑋2 𝑧 = 𝑧{ 𝑒−𝑗𝑤0𝑛 𝑢 𝑛 } = 𝑛=0
∞
𝑒−𝑗𝑤0𝑛 𝑧−𝑛
𝑋2 𝑧 = 𝑛=0
∞
(𝑒−𝑗𝑤0𝑧−1
)𝑛
=
1
1−(𝑒−𝑗𝑤0𝑧−1)
where |𝑒−𝑗𝑤0𝑧−1
| < 1
As 𝑒𝑗𝑤0 = 1 , ROC is |z|> 1](https://image.slidesharecdn.com/3dspunitiiisession2021-22-240108114546-f1ee9436/75/Frequency-Analysis-using-Z-Transform-pptx-41-2048.jpg)
![7 IT 01 Digital Signal Processing (Winter 2021) L25
Problems on Linearity Property
𝑿 𝒛 =
𝟏
𝟐
[𝒛(𝒆𝒋𝒘𝟎𝒏)+𝒛(𝒆𝒋𝒘𝟎𝒏)]
𝑋 𝑧 =
1
2
{
1
1−(𝑒𝑗𝑤0𝑧−1)
+
1
1−(𝑒−𝑗𝑤0𝑧−1)
}
Where ROC in both cases is |z|> 1
𝑋 𝑧 =
1
2
{
1−(𝑒−𝑗𝑤0𝑧−1+1−(𝑒𝑗𝑤0𝑧−1)
1−𝑒𝑗𝑤0𝑧−1 ∗(1−𝑒−𝑗𝑤0𝑧−1)
}
𝑋 𝑧 =
1
2
{
2−𝑒−𝑗𝑤0𝑧−1−𝑒𝑗𝑤0𝑧−1
1−𝑒𝑗𝑤0𝑧−1 ∗(1−𝑒−𝑗𝑤0𝑧−1)
}
Solving Numerator = 2 − 𝑒−𝑗𝑤0𝑧−1 − 𝑒𝑗𝑤0𝑧−1
= 2 −
2(𝑒𝑗𝑤0+𝑒−𝑗𝑤0) 𝑧−1
2
= 2 − 2 𝑐𝑜𝑠𝑤0𝑧−1](https://image.slidesharecdn.com/3dspunitiiisession2021-22-240108114546-f1ee9436/75/Frequency-Analysis-using-Z-Transform-pptx-42-2048.jpg)

![7 IT 01 Digital Signal Processing (Winter 2021) L25
Problems on Linearity Property
EX: Determine the z transform of signal 𝑥(𝑛) = (sin 𝑤0𝑛)u(n)
Solution : Given signal is 𝑥(𝑛) = (𝑠𝑖𝑛 𝑤0𝑛)u(n)
This signal can be decomposed by using Eular’s Identity as
sin 𝑤0𝑛 =
𝑒𝑗𝑤0𝑛 − 𝑒−𝑗𝑤0𝑛
2𝑗
So 𝑥(𝑛) = (
𝑒𝑗𝑤0𝑛−𝑒−𝑗𝑤0𝑛
2𝑗
)u(n)
Thus the decomposed signal is represented as
𝑥 𝑛 =
𝑒𝑗𝑤0𝑛
2𝑗
u n −
𝑒−𝑗𝑤0𝑛
2𝑗
u n
𝑋 𝑧 =
1
2𝑗
[𝑧(𝑒𝑗𝑤0𝑛)-𝑧(𝑒−𝑗𝑤0𝑛)]
We can write 𝑥1 = 𝑒𝑗𝑤0𝑛
𝑢(𝑛) and 𝑥2 = 𝑒−𝑗𝑤0𝑛
𝑢(𝑛)](https://image.slidesharecdn.com/3dspunitiiisession2021-22-240108114546-f1ee9436/75/Frequency-Analysis-using-Z-Transform-pptx-44-2048.jpg)
![7 IT 01 Digital Signal Processing (Winter 2021) L25
Problems on Linearity Property
𝑿 𝒛 =
𝟏
𝟐𝒋
[𝒛(𝒆𝒋𝒘𝟎𝒏)-𝒛(𝒆−𝒋𝒘𝟎𝒏)]
We can write 𝑥1 = 𝑒𝑗𝑤0𝑛𝑢(𝑛) and 𝑥2 = 𝑒−𝑗𝑤0𝑛𝑢(𝑛)
Let us say 𝛼 = 𝑒𝑗𝑤0 so 𝛼 = 𝑒𝑗𝑤0 = 1
𝑋1 𝑧 = 𝑧{ 𝑒𝑗𝑤0𝑛 𝑢 𝑛 } = 𝑛=0
∞
𝑒𝑗𝑤0𝑛 𝑧−𝑛
𝑋1 𝑧 = 𝑛=0
∞
(𝑒𝑗𝑤0𝑧−1
)𝑛
=
1
1−(𝑒𝑗𝑤0𝑧−1)
where |𝑒𝑗𝑤0𝑧−1
| < 1
As 𝑒𝑗𝑤0 = 1 , ROC is |z|> 1
Now let us say 𝛼 = 𝑒−𝑗𝑤0 so 𝛼 = 𝑒−𝑗𝑤0 = 1
𝑋1 𝑧 = 𝑧{ 𝑒−𝑗𝑤0𝑛 𝑢 𝑛 } = 𝑛=0
∞
𝑒−𝑗𝑤0𝑛 𝑧−𝑛
𝑋1 𝑧 = 𝑛=0
∞
(𝑒−𝑗𝑤0𝑧−1)𝑛 =
1
1−(𝑒−𝑗𝑤0𝑧−1)
where |𝑒−𝑗𝑤0𝑧−1| < 1
As 𝑒𝑗𝑤0 = 1 , ROC is |z|> 1](https://image.slidesharecdn.com/3dspunitiiisession2021-22-240108114546-f1ee9436/75/Frequency-Analysis-using-Z-Transform-pptx-45-2048.jpg)
![7 IT 01 Digital Signal Processing (Winter 2021) L25
Problems on Linearity Property
𝑿 𝒛 =
𝟏
𝟐𝒋
[𝒛(𝒆𝒋𝒘𝟎𝒏)-𝒛(𝒆−𝒋𝒘𝟎𝒏)]
𝑋 𝑧 =
1
2𝑗
{
1
1−(𝑒𝑗𝑤0𝑧−1)
−
1
1−(𝑒−𝑗𝑤0𝑧−1)
}
Where ROC in both cases is |z|> 1
𝑋 𝑧 =
1
2𝑗
{
1−𝑒−𝑗𝑤0𝑧−1−1+𝑒𝑗𝑤0𝑧−1)
1−𝑒𝑗𝑤0𝑧−1 ∗(1−𝑒−𝑗𝑤0𝑧−1)
}
𝑋 𝑧 =
1
2𝑗
{
−𝑒−𝑗𝑤0𝑧−1+𝑒𝑗𝑤0𝑧−1
1−𝑒𝑗𝑤0𝑧−1 ∗(1−𝑒−𝑗𝑤0𝑧−1)
}
Solving Numerator = 𝑒−𝑗𝑤0𝑧−1 − 𝑒𝑗𝑤0𝑧−1
=
(𝑒𝑗𝑤0−𝑒−𝑗𝑤0) 𝑧−1
2𝑗
= sin 𝑤0 𝑧−1](https://image.slidesharecdn.com/3dspunitiiisession2021-22-240108114546-f1ee9436/75/Frequency-Analysis-using-Z-Transform-pptx-46-2048.jpg)




















![7 IT 01 Digital Signal Processing (Winter 2021) L25
Problems on Diff. in z Domain Property
EX : Determine the z transform of the given signal 𝑥 𝑛 = 𝑛𝑎𝑛
𝑢(𝑛)
Solution : In this case we can write 𝑥 𝑛 = 𝑛 [𝑎𝑛𝑢 𝑛 ]
let 𝑥1 𝑛 = 𝑎𝑛𝑢(𝑛)
So 𝑥 𝑛 = 𝑛𝑥1(𝑛)
𝑋1 𝑧 =
1
1−𝑎𝑧−1 with ROC |z| > a
By using differentiation in z domain property z transform of 𝑛𝑥(𝑛) is
−𝑧
𝑑𝑋 𝑧
𝑑𝑧
so in this case 𝑧 𝑥 𝑛 = −𝑧
𝑑
𝑑𝑧
(
1
1−𝑎𝑧−1)
Using differentiation formula
𝑑
𝑑𝑧
𝑢
𝑣
=
𝑢.𝑑𝑣−𝑣.𝑑𝑢
𝑣2
We get X 𝑧 =
𝑎𝑧−1
(1−𝑎𝑧−1)2 with ROC |z| > a](https://image.slidesharecdn.com/3dspunitiiisession2021-22-240108114546-f1ee9436/75/Frequency-Analysis-using-Z-Transform-pptx-67-2048.jpg)
![7 IT 01 Digital Signal Processing (Winter 2021) L25
Problems on Diff. in z Domain Property
EX : Determine the z transform of the given signal 𝑥 𝑛 = 𝑛𝑎𝑛
𝑢(𝑛)
So : In this case we can write 𝑥 𝑛 = 𝑛 [𝑎𝑛𝑢 𝑛 ]let 𝑥1 𝑛 = 𝑎𝑛
𝑢(𝑛) , So 𝑥 𝑛 = 𝑛𝑥1(𝑛)
𝑋1 𝑧 =
1
1−𝑎𝑧−1 with ROC |z| > a
By using differentiation in z domain property z transform of 𝑛𝑥(𝑛) is
−𝑧
𝑑𝑋 𝑧
𝑑𝑧
so in this case 𝑧 𝑥 𝑛 = −𝑧
𝑑
𝑑𝑧
(
1
1−𝑎𝑧−1)
Using differentiation formula
𝑑
𝑑𝑧
𝑢
𝑣
=
𝑢.𝑑𝑣−𝑣.𝑑𝑢
𝑣2
We get X 𝑧 =
𝑎𝑧−1
(1−𝑎𝑧−1)2 with ROC |z| > a
If we consider a=1 we get a ramp signal 𝑥 𝑛 = 𝑛𝑢(𝑛)
So its z transform is X 𝑧 =
𝑧−1
(1−𝑧−1)2 with ROC |z| > 1](https://image.slidesharecdn.com/3dspunitiiisession2021-22-240108114546-f1ee9436/75/Frequency-Analysis-using-Z-Transform-pptx-68-2048.jpg)


























