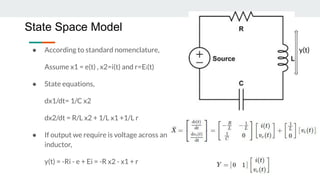
The document discusses state space analysis in electrical systems, introducing key concepts such as state variables, equations, and the mathematical modeling of energy storage in capacitors and inductors. It explains how state variables provide total information about a system's energy state and outlines the advantages and disadvantages of state models. Additionally, it highlights the applicability of state space methods to nonlinear, time-invariant, and multiple input-output systems.

1. State Space Analysis
Introduction and
Terminologies

2. Basic Laws of Physics
Set of Differential
Equations
State Space Method Transfer Function Method

3. Electrical System
● E(t) and I(t) are called characterising
variables
● Energy stored in capacitor
=1/2(CV^2)
● Energy stored in inductor= ½(LI^2)
I
e
Ei

4. ● e(t) and i(t) can be found for t>=0
● If initial energy state,
e(0) and i(0) as well as,
Ei(t) for t>=0 are known.
● So they can be defined as state variable.
● State variable:- They are set of characterising variable which gives you total
information about at any time instant t>=0, provided initial state and external
input are known to you.

5. ● From Basic laws of physics,
Ei = Ri + e + L di/dt
Also i=C de/dt.
● Mathematical Model,
de(t)/dt= 1/C i(t)
di/dt= R/L i(t) + 1/L e(t) + 1/L Ei(t)
Ei
i
e

6. ● According to standard nomenclature,
Assume x1 = e(t) , x2=i(t) and r=Ei(t)
● State equations,
dx1/dt= 1/C x2
dx2/dt = R/L x2 + 1/L x1 +1/L r
● If output we require is voltage across an
inductor,
y(t) = -Ri - e + Ei = -R x2 - x1 + r
State Space Model
y(t)

7. Mechanical System
Assume ,
x1=x(t) and x2=v(t)
● consider that we want to measure the position of the body. y=x1

8. Standard Format
Where ,
● x(t) : "state vector"
● y(t) : "output vector"
● u(t) : "input (or control) vector"
● A : "state (or system) matrix"
● B : “input matrix"
● C : "output matrix"
● D :"feedthrough (or
feedforward) matrix"

9. ● State variable defined are not unique. They can be defined by almost
infinite ways.
● We can define state variable according to our convenience.
Eg. Charge stored in capacitor.
● State variable formulation will give you unique output for given input.
Points to be considered

10. Advantages
● Complex techniques.
● Many computations are required.
● State model is not the unique
property of the system, because the
order of the state variables is not
important due to which state model
matrices get changed.
Disadvantages
● It can be applied to nonlinear
system.
● It can be applied to time invariant
systems.
● It can be applied to multiple input
multiple output systems.
● Its gives idea about the internal
state of the system.
● Can be used in time domain.

11. 1.