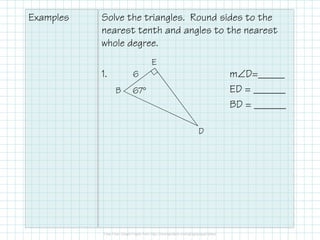
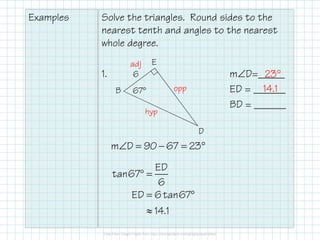
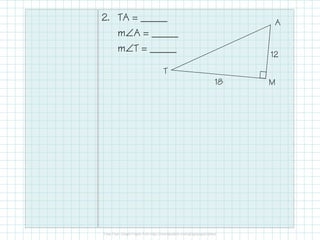
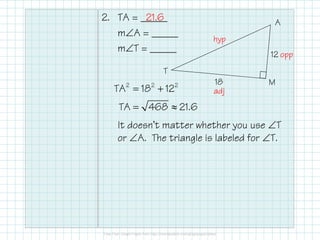
This document provides instructions for solving right triangles. It explains that to solve a right triangle, you find all the missing parts. If given an angle and side, you can use trig ratios to find the other acute angle and missing sides. If given two sides, you can use the Pythagorean theorem to find the missing side and trig ratios to find an angle. It provides examples of solving right triangles when given an angle and side or two sides.

1. 4.11.5 Solving Right Triangles
The student is able to (I can):
• Find the missing parts of a right triangle
• Use trig ratios to solve problems

2. To “solve” a right triangle means to find all
of the missing parts of the right triangle.
If you are given an angle and a side:
• Subtract the angle from 90° to find the
other acute angle
• Use trig ratios to find one of the missing
sides
• Use either trig ratios or Pythagorean
Theorem to find the third side

3. If you are given two sides:
• Use Pythagorean Theorem to find the
missing side
• Use trig ratios to find an angle
— Unless all of your sides work out to
be whole numbers, be sure to use the
two given sides in your trig ratio to
prevent rounding errors.
• Subtract the angle you found from 90°
to find the other angle

4. Examples Solve the triangles. Round sides to the
nearest tenth and angles to the nearest
whole degree.
1. m∠D=_____
ED = ______
BD = ______
6
67°B
E
D

5. Examples Solve the triangles. Round sides to the
nearest tenth and angles to the nearest
whole degree.
1. m∠D=_____
ED = ______
BD = ______
6
67°B
E
D
adj
opp
hyp
ED
tan67
6
ED 6tan67
14.1
° =
= °
≈
m D 90 67 23∠ = − = °
23°
14.1

6. Examples Solve the triangles. Round sides to the
nearest tenth and angles to the nearest
whole degree.
1. m∠D=_____
ED = ______
BD = ______
6
67°B
E
D
adj
opp
hyp
ED
tan67
6
ED 6tan67
14.1
° =
= °
≈
m D 90 67 23∠ = − = °
2 2 2
BD 6 14.1
BD 234.81
15.3
= +
=
≈
23°
14.1
15.3

7. 2. TA = _____
m∠A = _____
m∠T = _____
12
18
T
A
M

8. 2. TA = _____
m∠A = _____
m∠T = _____
It doesn’t matter whether you use ∠T
or ∠A. The triangle is labeled for ∠T.
12
18
T
A
M2 2 2
TA 18 12
TA 468 21.6
= +
= ≈
hyp
opp
adj
21.6

9. 2. TA = _____
m∠A = _____
m∠T = _____
It doesn’t matter whether you use ∠T
or ∠A. The triangle is labeled for ∠T.
12
18
T
A
M2 2 2
TA 18 12
TA 468 21.6
= +
= ≈
hyp
opp
adj
1
12
tanT
18
12
T tan
18
34
−
=
 =  
 
≈ °
m A 90 34
56
∠ = −
= °
21.6
56°
34°