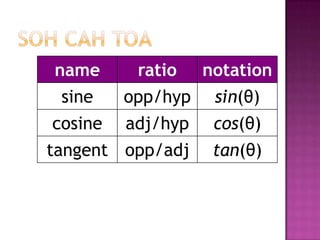
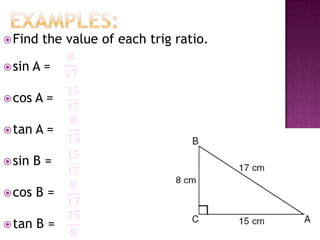
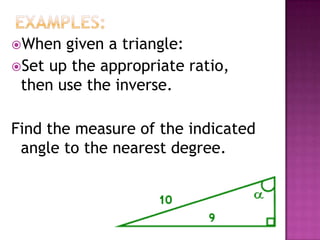
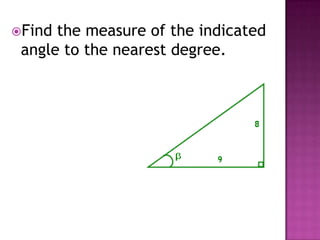
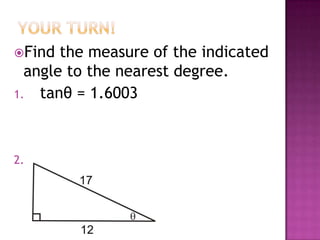
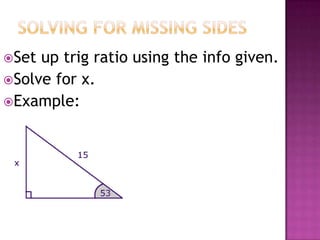
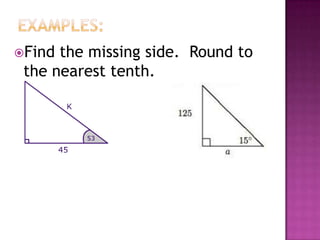
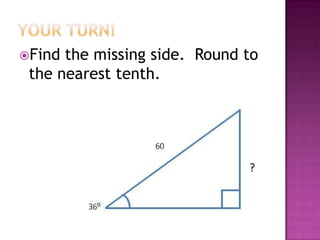
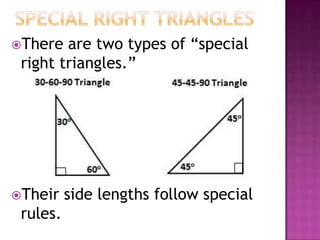
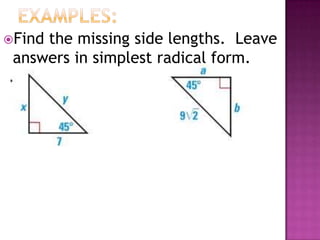
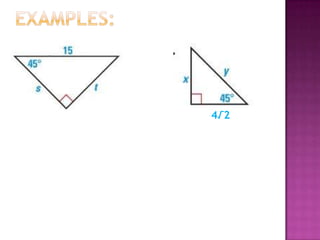
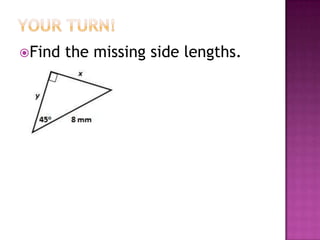
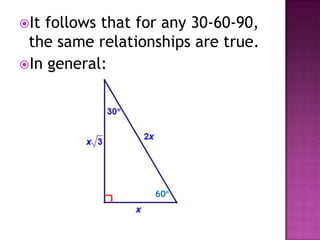
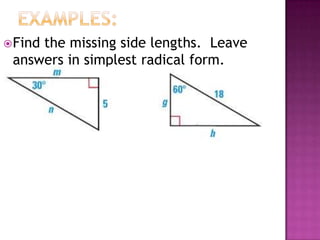
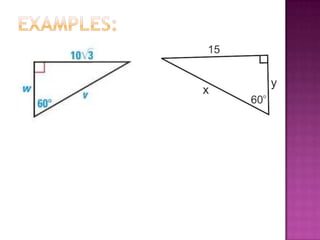
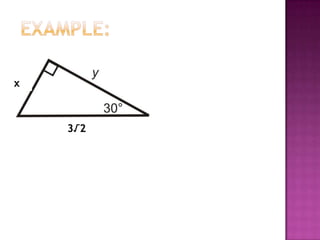
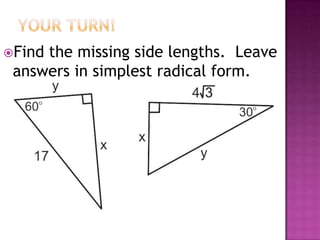
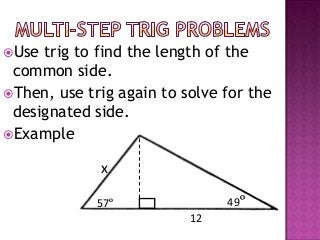
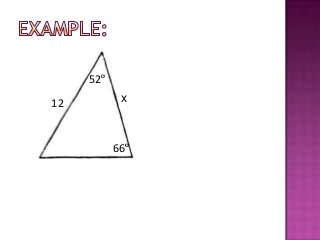
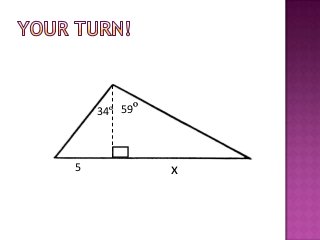
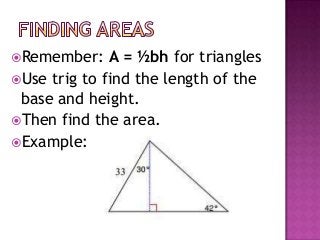
The document provides information on trigonometric ratios and how to use them to solve for missing angles and sides of right triangles. It defines the sine, cosine, and tangent ratios using opposite, adjacent, and hypotenuse side lengths relative to a designated angle θ. It gives examples of setting up and evaluating trig ratios, finding missing sides and angles of triangles using inverse trig functions, and solving application problems involving angles of elevation/depression.

2. Trigonometric ratios are used with
right triangles to solve for missing
angles and/or sides.
The 3 main trig ratios are:
Sine
Cosine
Tangent

3. Sides are labeled in reference to a
designated angle, θ (“theta”)
Hypotenuse: the longest side. Always
opposite the right angle.
Adjacent: side that is
touching the angle θ.
Opposite: side across
from the angle θ.

4. name ratio notation
sine opp/hyp sin(θ)
cosine adj/hyp cos(θ)
tangent opp/adj tan(θ)

5. Set up the ratio using the
correct side lengths.
Reduce if possible.
OR – divide and round your
answer.
Depends on the directions given.

6.  Find the value of each trig ratio.
 sin A=
 cos A=
 tan A=
 sin B=
 cos B=
 tan B=

7. Find the value of each trig ratio to
the nearest ten-thousandth.
sin R=
cos R=
tan S=

8. Inverse trig ratios are used to solve
for missing angle measures.
They include:
sin-1
cos-1
tan-1
On your calculator: hit “2nd” and
then the trig button you need

9. When given a decimal value:
Find each angle measure to the
nearest degree.
sinθ = 0.7193
cosθ = 0.3907
tanθ = 0.6009

10. When given a triangle:
Set up the appropriate ratio,
then use the inverse.
Find the measure of the indicated
angle to the nearest degree.

11. Find the measure of the indicated
angle to the nearest degree.

12. Find the measure of the indicated
angle to the nearest degree.
1. tanθ = 1.6003
2.

13. Set up trig ratio using the info given.
Solve for x.
Example:

14. Find the missing side. Round to
the nearest tenth.

15. Find the missing side. Round to
the nearest tenth.

16. There are two types of “special
right triangles.”
Their side lengths follow special
rules.

17. Wecan use the Pythagorean
Theorem to verify the length of the
hypotenuse if both legs are 1.

18. It follows that for any 45-45-90,
the same relationships are true.
In general:

19. Findthe missing side lengths. Leave
answers in simplest radical form.

20. 4√2

21. Find the missing side lengths.

22. A 30-60-90 is half of an equilateral
triangle.
That means the hypotenuse is twice
the short leg.
We can use the Pythagorean
Theorem to find the long leg.

23. It follows that for any 30-60-90,
the same relationships are true.
In general:
60º

24.  Find
the missing side lengths. Leave
answers in simplest radical form.

26. x
3√2

27. Findthe missing side lengths. Leave
answers in simplest radical form.

28. Use trig to find the length of the
common side.
Then, use trig again to solve for the
designated side.
Example
x
57º 49º
12

29. 52º
12 x
66º

30. 34º 59º
5 x

31. Remember: A = ½bh for triangles
Use trig to find the length of the
base and height.
Then find the area.
Example:

32.  Hints for successful problem solving:
 Draw a picture!
 Label all given information.
 Mark the angles or sides you need to find.
Use a different variable for each quantity.
 Create a game plan!
 Solve using trig.
 Check that your answer is reasonable.
The hypotenuse is always the longest
side!

33. Angle of elevation – measured
upward from the horizontal.
Angle of depression – measured
downward from the horizontal.

34. A light house is 60 meters high with its
base at sea level. From the top of the
lighthouse, the angle of depression of a
boat is 15 degrees.
A. How far is the boat from the foot of
the light house?
B. How far is the boat from the top of
the lighthouse?

35.  Katieand Sara are attending a theater
performance. From her seat, Katie looks
down at an angle of 18 degrees to see
the orchestra pit. Sara's seat is in the
balcony directly above Katie. Sara looks
down at an angle of 42 degrees to see
the pit. The horizontal distance from
Katie's seat to the pit is 46 ft. What is
the vertical distance between Katie's
seat and Sara's seat?