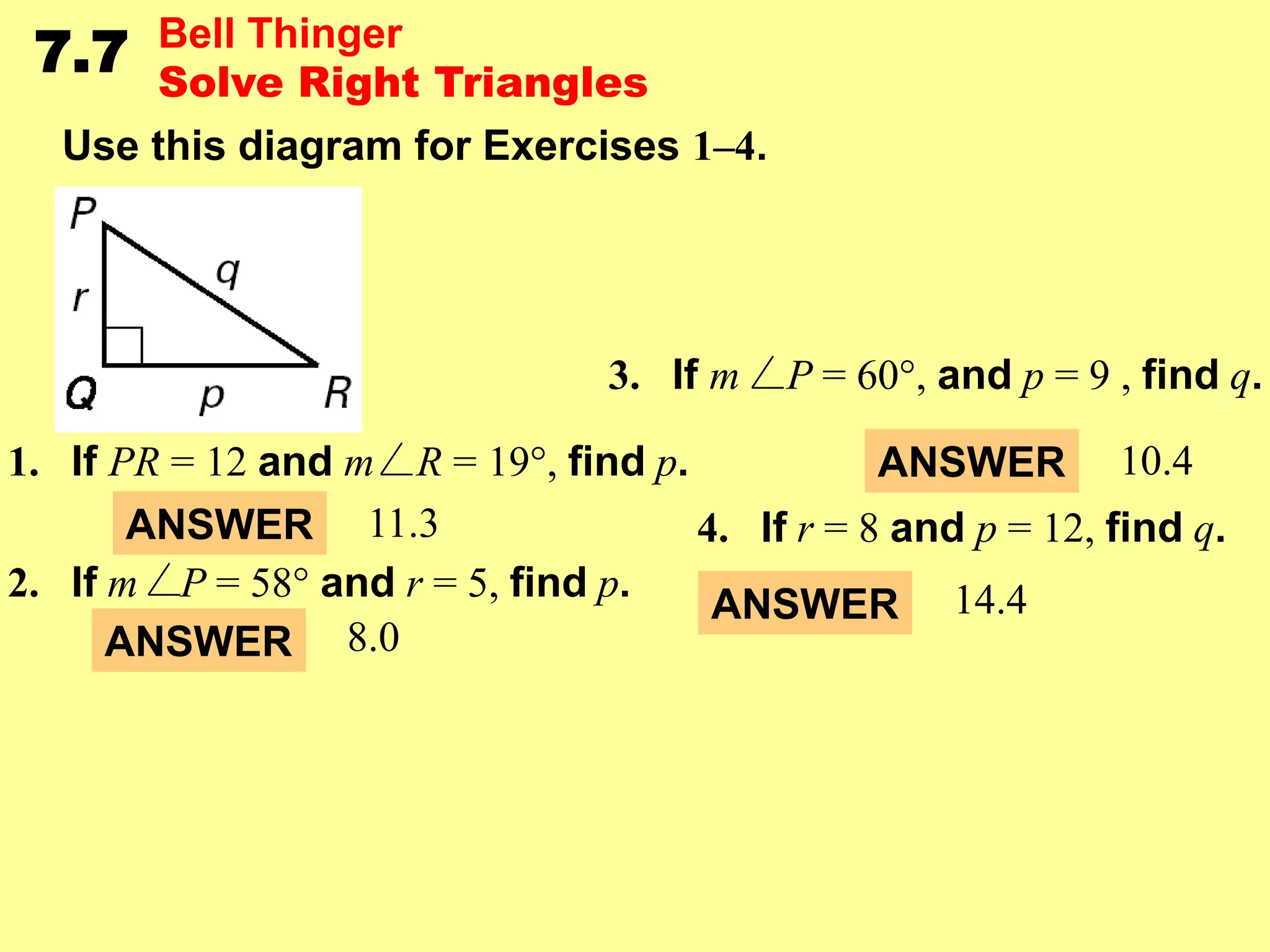
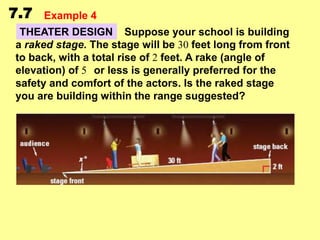
This document contains examples and exercises about solving right triangles using trigonometric ratios and inverse trigonometric functions with a calculator. It includes examples finding unknown side lengths and angle measures of right triangles given certain ratios. Students are guided through setting up and solving right triangle problems. Practice problems are provided for students to work through on their own.

1. Bell Thinger
7.7 Solve Right Triangles
Use this diagram for Exercises 1–4.
3. If m
P = 60°, and p = 9 , find q.
1. If PR = 12 and m R = 19°, find p.
ANSWER 10.4
ANSWER 11.3
4. If r = 8 and p = 12, find q.
2. If m P = 58° and r = 5, find p.
ANSWER 14.4
ANSWER 8.0

2. 7.7
Example 1
Use a calculator to approximate the
measure of A to the nearest tenth
of a degree.
SOLUTION
Because tan A =
15
3
=
= 0.75, tan–1 0.75 = m
20
4
Use a calculator.
tan –1 0.75
36.86989765. . .
So, the measure of
A is approximately 36.9 .
A

3. 7.7
Example 2
Let A and
B be acute angles in a right triangle.
Use a calculator to approximate the measures of A
and
B to the nearest tenth of a degree.
a. sin A = 0.87
b. cos B = 0.15
SOLUTION
a. m
A
= sin –1 0.87
60.5
b. m
B
= cos –1 0.15
81.4°

4. 7.7
Guided Practice
1. Look back at Example 1. Use a calculator and an
inverse tangent to approximate m
C to the
nearest tenth of a degree.
ANSWER
53.1
2. Find m D to the nearest tenth of a degree if
sin D = 0.54.
ANSWER
32.7°

5. 7.7
Example 3
Solve the right triangle. Round
decimal answers to the nearest
tenth.
SOLUTION
STEP 1
Find mB by using the Triangle Sum Theorem.
180 = 90 + 42° + mB
48° = mB

6. 7.7
Example 3
STEP 2
Approximate BC by using a tangent ratio.
tan 42 = BC
70
70 tan 42° = BC
Write ratio for tangent of 42 .
Multiply each side by 70.
70 0.9004
BC
Approximate tan 42°.
63
BC
Simplify and round answer.

7. 7.7
Example 3
STEP 3
Approximate AB by using a cosine ratio.
cos 42 = 70
Write ratio for cosine of 42o.
AB
AB cos 42° =
70
70
AB = cos 42°
70
AB
0.7431
AB
94.2
Multiply each side by AB.
Divide each side by cos 42o.
Use a calculator to find cos 42o.
Simplify .
The angle measures are 42°, 48°, and 90°. The side
lengths are 70 feet, about 63 feet, and about 94 feet.

8. 7.7
Example 4
THEATER DESIGN Suppose your school is building
a raked stage. The stage will be 30 feet long from front
to back, with a total rise of 2 feet. A rake (angle of
elevation) of 5 or less is generally preferred for the
safety and comfort of the actors. Is the raked stage
you are building within the range suggested?

9. 7.7
Example 4
SOLUTION
Use the sine and inverse sine ratios to find the degree
measure x of the rake.
sin x = opp. = 2
hyp
30
x
sin –1 0.0667
0.0667
3.842
The rake is about 3.8 , so it is within the suggested
range of 5° or less.

10. 7.7
Guided Practice
3. Solve a right triangle that has a 40 angle and a
20 inch hypotenuse.
ANSWER
40°, 50°, and 90°, about 12.9 in., about 15.3 in., and 20 in.
4. WHAT IF? In Example 4, suppose another raked
stage is 20 feet long from front to back with a total
rise of 2 feet. Is this raked stage safe? Explain.
ANSWER
No; the rake is 5.7° so it is slightly larger than the
suggested range.

11. 7.7
Exit Slip
Use this diagram for exercises 1-3.
1.
If x = 9 and z = 11 find m
degree.
ANSWER 54.9
X to the nearest tenth of a

12. 7.7
Exit Slip
Use this diagram for exercises 1-3.
2.
If y = 5 and z = 12 find m
degree.
ANSWER 65.4
X to the nearest tenth of a

13. 7.7
Exit Slip
Use this diagram for exercises 1-3.
3.
If m
Y = 17.4 and z = 12 solve ∆XYZ.
ANSWER
The angles are 17.4°, 72.6°, and 90°; the sides are 12,
about 3.6, and about 11.5.

14. 7.7
Homework
Pg 505-507
#6, 7, 10, 14, 34