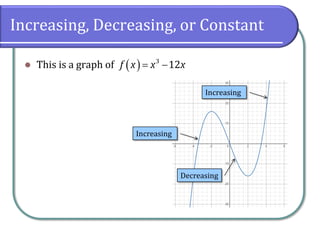
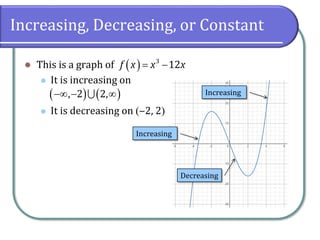
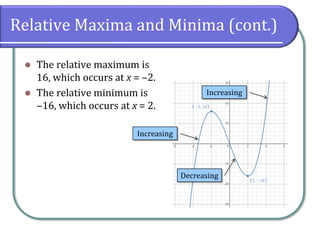
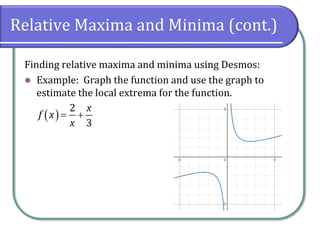
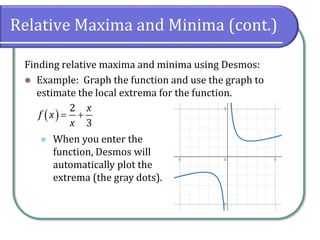
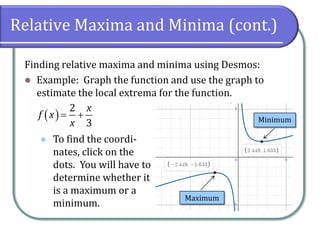
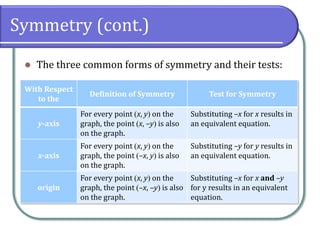
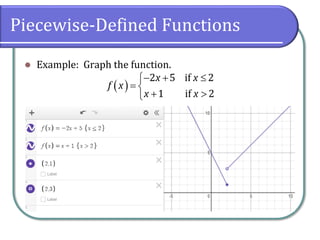
This document discusses functions and their graphs. It defines increasing, decreasing and constant functions based on how the function values change as the input increases. Relative maxima and minima are points where a function changes from increasing to decreasing. Symmetry of functions is classified by the y-axis, x-axis and origin. Even functions are symmetric about the y-axis, odd functions are symmetric about the origin. Piecewise functions have different definitions over different intervals.

1. 2.2 More on Functions and
Their Graphs
Chapter 2 Functions and Graphs

2. Concepts and Objectives
⚫ The objectives for this section are
⚫ Identify intervals on which a function increases,
decreases, or is constant
⚫ Use graphs to locate relative maxima or minima
⚫ Test for symmetry
⚫ Identify even or odd functions and recognize their
symmetries
⚫ Understand and use piecewise functions

3. Increasing, Decreasing, or Constant
⚫ We say that a function is increasing on an interval if the
function values increase as the input values increase
within that interval.
⚫ Similarly, a function is decreasing on an interval if the
function values decrease as the input values increase
over that interval.
⚫ If a function is neither increasing nor decreasing on an
interval (a horizontal line), then it is constant as the
input values do not change over that interval.

4. Increasing, Decreasing, or Constant
⚫ This is a graph of ( ) 3
12
f x x x
= −
Increasing
Increasing
Decreasing

5. Increasing, Decreasing, or Constant
⚫ This is a graph of
⚫ It is increasing on
⚫ It is decreasing on (‒2, 2)
( ) 3
12
f x x x
= −
Increasing
Increasing
Decreasing
( ) ( )
, 2 2,
− − 

6. Relative Maxima and Minima
⚫ A value of the input where a function changes from
increasing to decreasing (as the input variable
increases) is the location of a relative maximum.
⚫ If a function has more than one, we say it has relative
maxima.
⚫ Similarly, a value of the input where a function changes
from decreasing to increasing as the input variable
increases is the location of a relative minimum (plural
minima).
⚫ Sometimes the word local is used instead of relative.

7. Relative Maxima and Minima (cont.)
⚫ The relative maximum is
16, which occurs at x = ‒2.
⚫ The relative minimum is
‒16, which occurs at x = 2.
Increasing
Increasing
Decreasing

8. Relative Maxima and Minima (cont.)
Finding relative maxima and minima using Desmos:
⚫ Example: Graph the function and use the graph to
estimate the local extrema for the function.
( )
2
3
x
f x
x
= +

9. Relative Maxima and Minima (cont.)
Finding relative maxima and minima using Desmos:
⚫ Example: Graph the function and use the graph to
estimate the local extrema for the function.
⚫
( )
2
3
x
f x
x
= +
When you enter the
function, Desmos will
automatically plot the
extrema (the gray dots).

10. Relative Maxima and Minima (cont.)
Finding relative maxima and minima using Desmos:
⚫ Example: Graph the function and use the graph to
estimate the local extrema for the function.
⚫
( )
2
3
x
f x
x
= +
To find the coordi-
nates, click on the
dots. You will have to
determine whether it
is a maximum or a
minimum.
Minimum
Maximum

11. Symmetry
⚫ The word symmetry comes from the Greek symmetria,
meaning “the same measure”. Three different types of
symmetry are shown below.
⚫ Notice that a graph does not have to be a function to be
symmetrical (b).

12. Symmetry (cont.)
⚫ The three common forms of symmetry and their tests:
With Respect
to the
Definition of Symmetry Test for Symmetry
y-axis
For every point (x, y) on the
graph, the point (x, –y) is also
on the graph.
Substituting –x for x results in
an equivalent equation.
x-axis
For every point (x, y) on the
graph, the point (–x, y) is also
on the graph.
Substituting –y for y results in
an equivalent equation.
origin
For every point (x, y) on the
graph, the point (–x, –y) is also
on the graph.
Substituting –x for x and –y
for y results in an equivalent
equation.

13. Symmetry
⚫ Example: Test for symmetry with respect to the y-axis
and the x-axis.
a) b)
2
4
y x
= + 2 4
x y
+ =

14. Symmetry
⚫ Example: Test for symmetry with respect to the y-axis
and the x-axis.
a) b)
2
4
y x
= + 2 4
x y
+ =
( )
2
4
y x
= − +
2
4
y x
= +
2
4
y x
− = +
Symmetric about the
y-axis, not symmetric
about the x-axis.

15. Symmetry
⚫ Example: Test for symmetry with respect to the y-axis
and the x-axis.
a) b)
2
4
y x
= + 2 4
x y
+ =
( )
2
4
y x
= − +
2
4
y x
= +
2
4
y x
− = +
( )
2 4
x y
− + =
2 4
x y
− + =
( )
2 4
x y
+ − =
2 4
x y
− =
Symmetric about the
y-axis, not symmetric
about the x-axis.
Not symmetric about
either axis.

16. Symmetry (cont.)
⚫ Example: Is the following graph symmetric with respect
to the origin?
3
y x
=
( )
3
y x
− = −
3
y x
− = −
3
y x
=

17. Even and Odd Functions
⚫ We have seen that if a graph is symmetric with respect
to the x-axis, it usually fails the vertical line test and is
therefore not a function.
⚫ However, many functions have graphs that are
symmetric with respect to the y-axis or the origin. These
functions are classified as even or odd functions.
⚫ It is possible for a function to be neither even nor odd.
Also, remember that this only applies to functions.
Even function
Symmetric about the
y-axis
Odd function
Symmetric about the
origin
( ) ( )
f x f x
− =
( ) ( )
f x f x
− = −

18. Even and Odd Functions (cont.)
Example: Decide whether each function is even, odd, or
neither.
a) ( ) 4 2
8 3
f x x x
= −

19. Even and Odd Functions (cont.)
Example: Decide whether each function is even, odd, or
neither.
a) ( ) 4 2
8 3
f x x x
= −
( ) ( ) ( )
4 2
8 3
f x x x
− = − − −
4 2
8 3
x x
= − ( ) ( ): even
f x f x
− =

20. Even and Odd Functions (cont.)
b) c)
( ) 3
6 9
f x x x
= +
3
6 9
x x
= − −
( )
3
6 9
x x
= − +
( ) ( ): odd
f x f x
− = −
( ) 2
3 5
f x x x
= +

21. Even and Odd Functions (cont.)
b) c)
( ) 3
6 9
f x x x
= + ( ) 2
3 5
f x x x
= +

22. Even and Odd Functions (cont.)
b) c)
( ) 3
6 9
f x x x
= +
( ) ( ) ( )
3
6 9
f x x x
− = − + −
3
6 9
x x
= − −
( )
3
6 9
x x
= − +
( ) ( ): odd
f x f x
− = −
( ) 2
3 5
f x x x
= +

23. Even and Odd Functions (cont.)
b) c)
⚫ What do you notice about the exponents and the
function’s being called even, odd, or neither?
( ) 3
6 9
f x x x
= +
( ) ( ) ( )
3
6 9
f x x x
− = − + −
3
6 9
x x
= − −
( )
3
6 9
x x
= − +
( ) ( ): odd
f x f x
− = −
( ) 2
3 5
f x x x
= +
( ) ( ) ( )
2
3 5
f x x x
− = − + −
2
3 5
x x
= −
( ) ( )
f x f x
− 
( ) ( )
f x f x
−  −
neither

24. Piecewise-Defined Functions
⚫ Some functions, such as the absolute value function, are
defined by different rules over different intervals of their
domains. Such functions are called piecewise-defined
functions.
⚫ If you are graphing a piecewise function by hand, graph
each piece over its defined interval. If necessary, use
open and closed circles to mark discontinuities.

25. Piecewise-Defined Functions
⚫ If you are using Desmos to graph a piecewise function:
⚫ Use one line for each piece. You can either call it y or
use the function name.
⚫ You can control the interval graphed by putting
braces after the function and defining the intervals
over which it is defined.
⚫ You can make open and closed circles by plotting the
points separately and changing the type of point used
by clicking on the setup wheel.

26. Piecewise-Defined Functions
⚫ Example: Graph the function.
( )
2 5 if 2
1 if 2
x x
f x
x x
− + 

= 
+ 


27. Evaluating a Piecewise Function
⚫ To evaluate a piecewise function for a given value, you
have to determine into which given interval your value
of x falls. Once you have done that, substitute your x into
that piece.
⚫ Example: Given the function,
Evaluate
( )
3 5 if 0
4 7 if 0
x x
f x
x x
+ 

= 
+ 

( ) ( )
0 and 3
f f

28. Evaluating a Piecewise Function
⚫ Example: Given the function,
Evaluate
–2 is less than 0, so we will use the first expression.
0 is greater than or equal to 0, so we use the second.
( )
3 5 if 0
4 7 if 0
x x
f x
x x
+ 

= 
+ 

( ) ( )
2 and 0
f f
−
( )
3 2 5 1
− + = −
( )
4 0 7 7
+ =

29. For Next Class
⚫ Section 2.2 in MyMathLab
⚫ Quiz 2.2 in Canvas
⚫ Optional: Read section 2.5 in your textbook