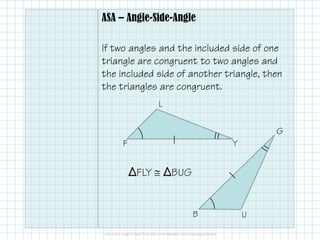
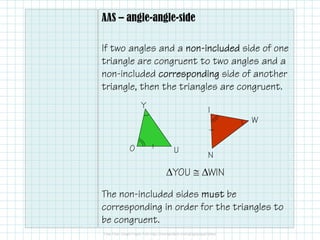
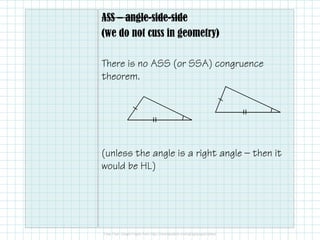
This document discusses two theorems for proving triangles are congruent: Angle-Side-Angle (ASA) and Angle-Angle-Side (AAS). For ASA, if two angles and the included side of one triangle are equal to those of another triangle, then the triangles are congruent. For AAS, if two angles and a non-included side of one triangle are equal to those of another, and the non-included sides are corresponding, then the triangles are congruent. It also notes there is no Angle-Side-Side (ASS) congruence theorem.

1. Congruent Triangles Part 2
The student is able to (I can):
• Identify and prove congruent triangles given
— Two angles and a side (Angle-Side-Angle and Angle-
Angle-Side)

2. ASA – Angle-Side-Angle
If two angles and the included side of one
triangle are congruent to two angles and
the included side of another triangle, then
the triangles are congruent.
F
L
Y
B U
G
ΔFLY ≅ ΔBUG

3. AAS – angle-angle-side
If two angles and a nonnonnonnon----includedincludedincludedincluded side of one
triangle are congruent to two angles and a
non-included correspondingcorrespondingcorrespondingcorresponding side of another
triangle, then the triangles are congruent.
The non-included sides mustmustmustmust be
corresponding in order for the triangles to
be congruent.
N
I
W
UO
Y
∆YOU ≅ ∆WIN

4. ASS – angle-side-side
(we do not cuss in geometry)
There is no ASS (or SSA) congruence
theorem.
(unless the angle is a right angle — then it
would be HL)