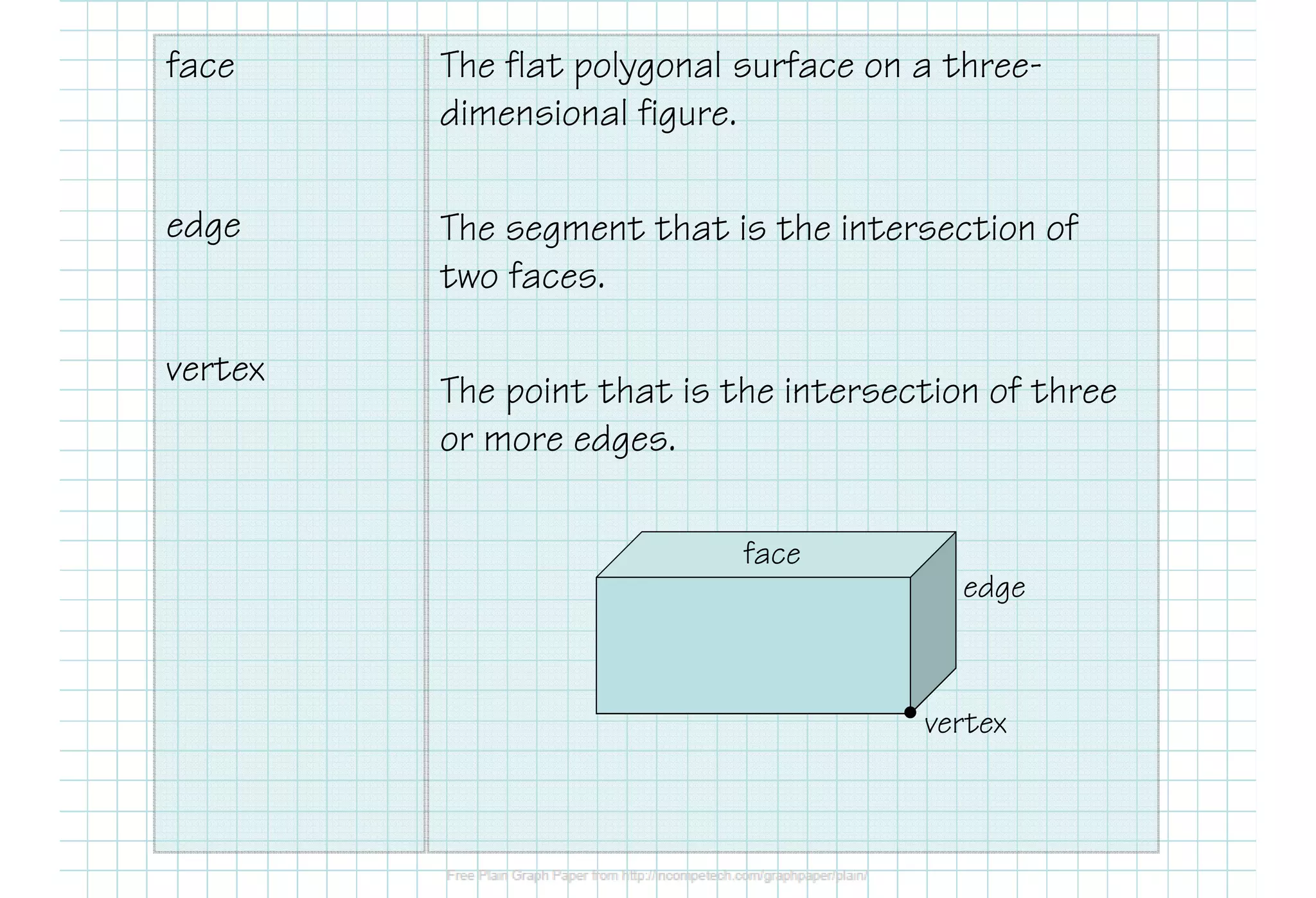
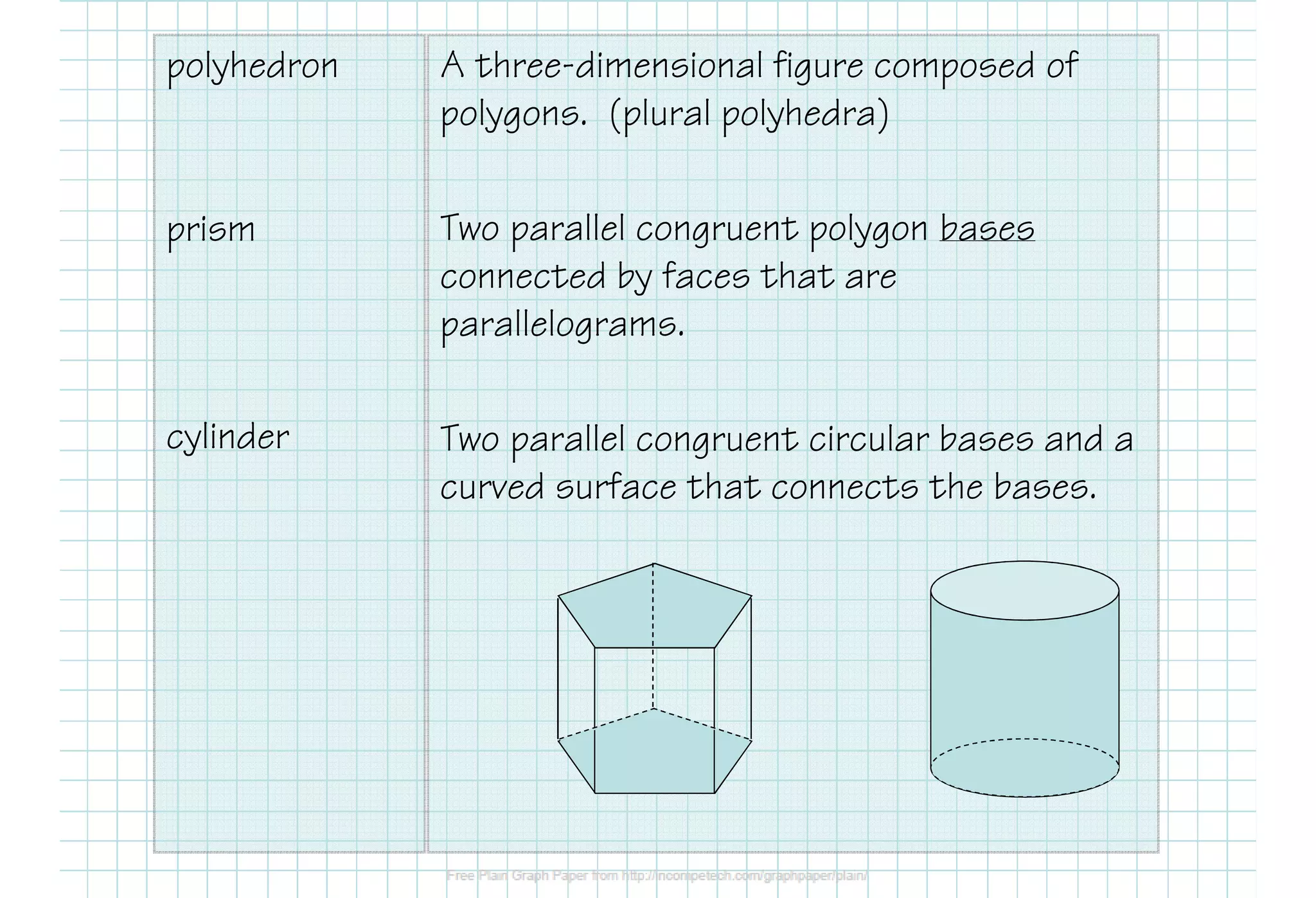
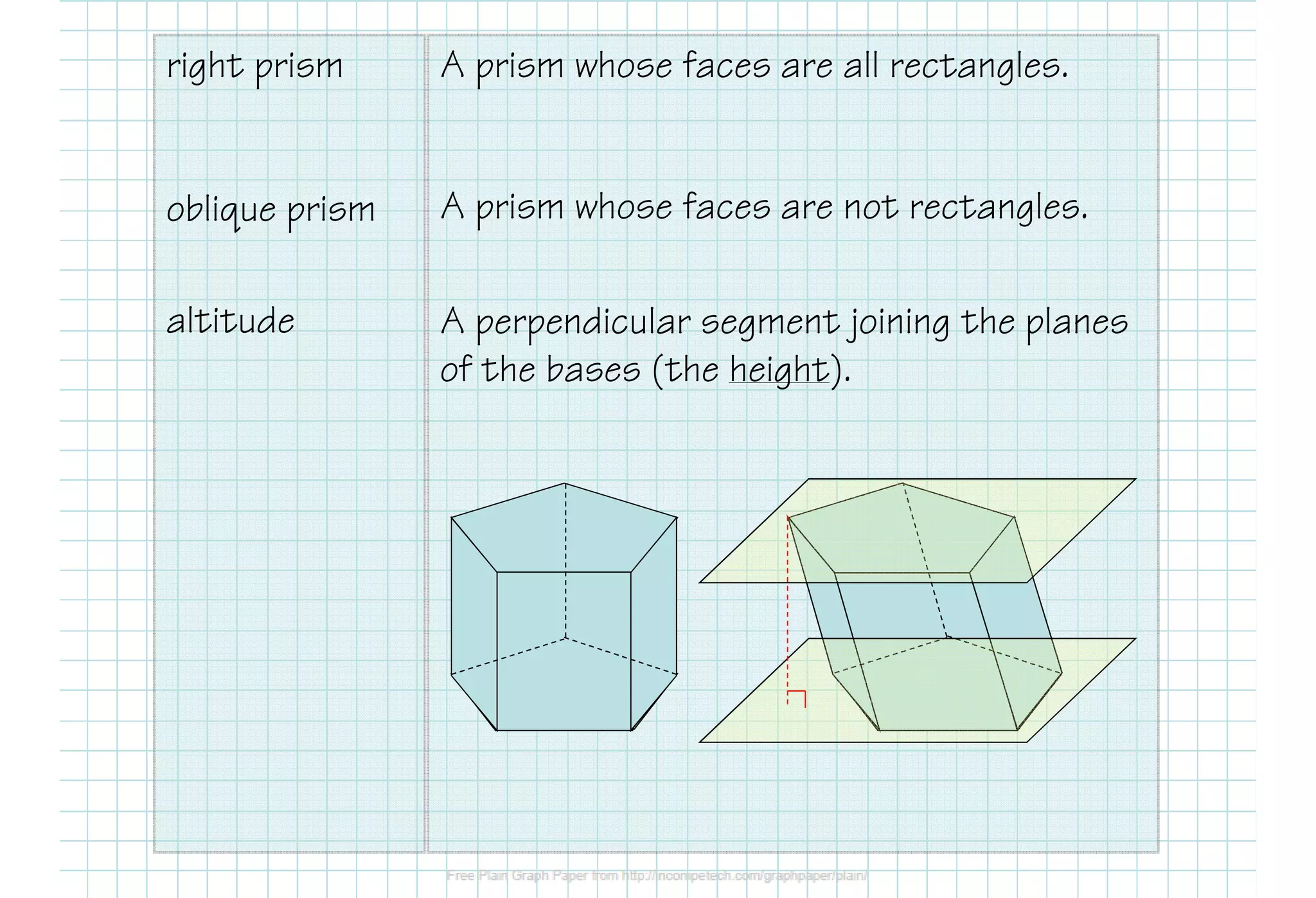
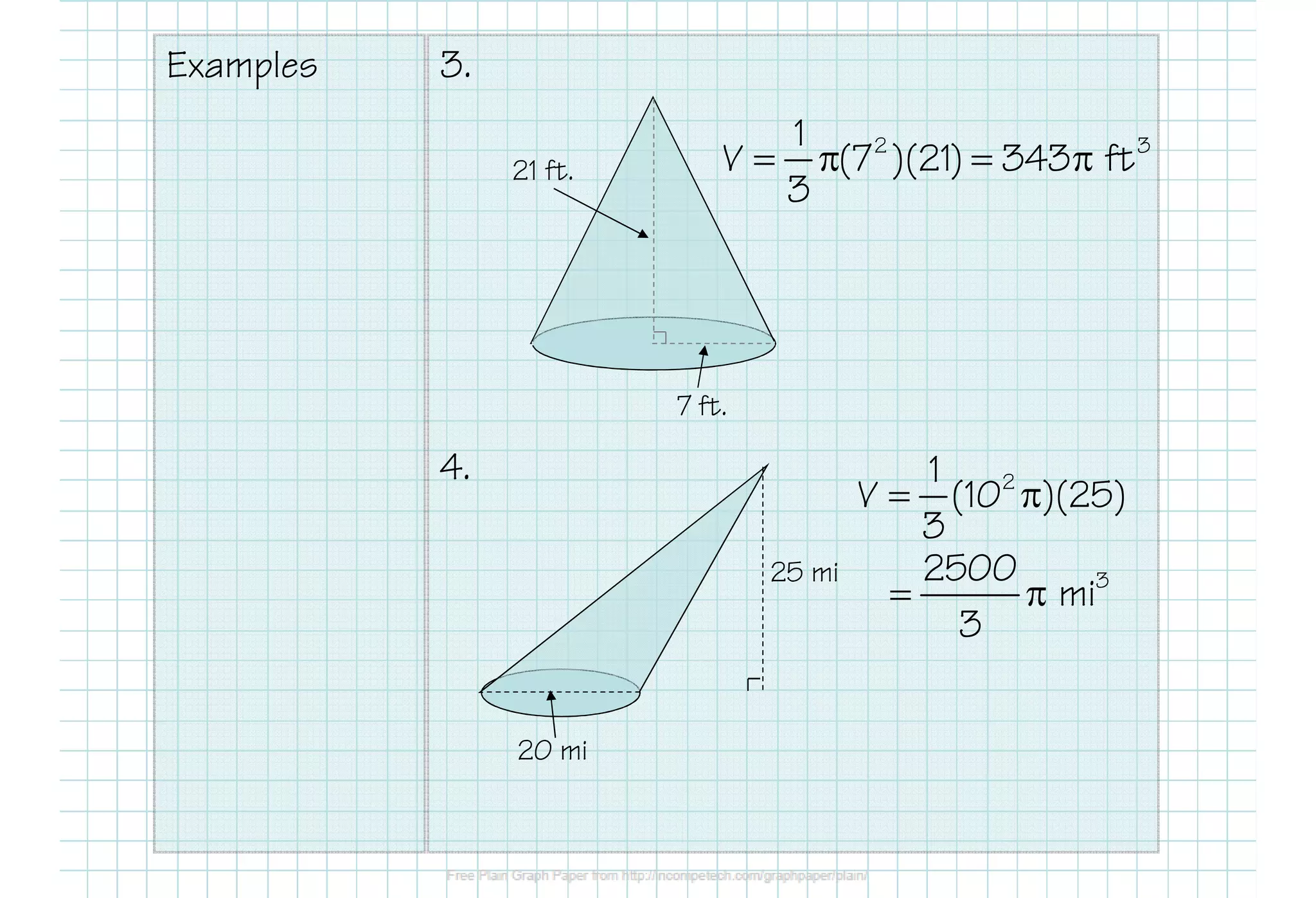
This document defines various 3D shapes and their volume formulas. It discusses how to calculate the volume of prisms, cylinders, pyramids, and cones. For prisms and cylinders, the volume is the area of the base multiplied by the height, regardless of whether the shape is right or oblique. The volume of a pyramid is one-third the area of the base multiplied by the height. For a cone, the volume is one-third pi times the area of the base times the height. Several examples are provided to demonstrate calculating volumes of different 3D shapes using the appropriate formulas.

1. 5.13.4 Volume
The student is able to (I can):
• Calculate the volume of prisms, cylinders, pyramids, and
cones

2. face
edge
vertex
The flat polygonal surface on a three-
dimensional figure.
The segment that is the intersection of
two faces.
The point that is the intersection of three
or more edges.
face
edge
vertex•

3. polyhedron
prism
cylinder
A three-dimensional figure composed of
polygons. (plural polyhedra)
Two parallel congruent polygon bases
connected by faces that are
parallelograms.
Two parallel congruent circular bases and a
curved surface that connects the bases.

4. pyramid
cone
A polygonal base with triangular faces that
meet at a common vertex.
A circular base and a curved surface that
connects the base to a vertex.

5. right prism
oblique prism
altitude
A prism whose faces are all rectangles.
A prism whose faces are not rectangles.
A perpendicular segment joining the planes
of the bases (the height).

6. Volume Let’s consider a deck of cards. If a deck is
stacked neatly, it resembles a right
rectangular prism. The volume of the prism
is
V = Bh,
where B is the area of one card, and h is
the height of the deck.
If we shift the deck so
that it becomes an
oblique prism, does it
have the same number
of cards?

7. For any prism, whether right or oblique, the
volume is
V = Bh
where h is the altitude, not the length of
the lateral edge.

8. Likewise, for cylinders, it doesn’t matter
whether the cylinder is right or oblique, the
volume is
V = Bh = πr2h

9. Examples Find the volume of each figure:
1.
2.
10 ft.
8 ft.
3 m
19 m
( )2 2
B 3 9 m= π = π
3
V (9 )(19) 171 m= π = π
( )( )= =
 
 
 
2
5 10
B 172.05
180
4 tan
5
V = (172)(8) = 1376 ft3

10. The volume of a pyramid with base area B
and height h is
1
V Bh
3
=
The volume of a cone is
21 1
V Bh r h
3 3
= = π

11. Examples Find the volume of the following:
1.
2.
2
22 3
B 3 yd
4
= =
= = 31
V ( 3)(3) 3 yd
3
10 mm
10 mm
13 mm
5 mm
12 mm
(Pyth. triple)
21
V (10 )(12)
3
=
3
400 mm=
2 yd
3 yd
2 yd

12. Examples 3.
4.
7 ft.
21 ft.
2 31
V (7 )(21) 343 ft
3
= π = π
25 mi
20 mi
21
V (10 )(25)
3
= π
32500
mi
3
= π