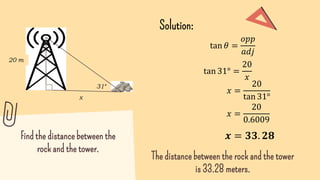
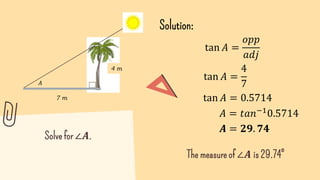
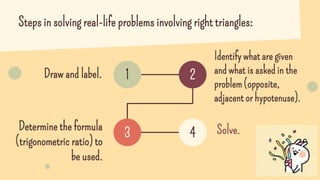
This document provides a lesson on solving word problems involving right triangles using trigonometric ratios. It begins with reviewing trigonometric functions and their inverses. An example word problem is then presented about finding the width of a river using a 5m log at a 75 degree angle. The lesson shows how to set up and solve similar word problems by identifying trigonometric ratios, labeling diagrams, and calculating missing values. Students are given practice problems and encouraged to draw diagrams to set up and solve real-world scenarios involving right triangles.

1. WORD PROBLEMS
INVOLVING RIGHT
TRIANGLES
By Rhea Ann N. Diaz

2. REVIEW
01
Please take out your scientific calculator.

3. Find the value of the following, correct to four decimal places.
Sin 38° =
0.6157
Cos 75 ° =
0.2588
Tan 26 ° =
0.4877
Cos 54 ° =
0.5878
Tan 33 ° =
0.6494

4. Find the measure of the following angles to the nearest
hundredths.
A = 31.94 °
Sin A = 0.529
A = 𝒔𝒊𝒏−𝟏
𝟎. 𝟓𝟐𝟗
Cos B = 0.49
B = 𝒄𝒐𝒔−𝟏 𝟎. 𝟒𝟗
B = 60.66°
Tan C = 1.8
C = 𝒕𝒂𝒏−𝟏𝟏. 𝟖
C = 60.95 °
Sin D = 0.256
D = 𝒔𝒊𝒏−𝟏𝟎. 𝟐𝟓𝟔
D = 14.83 °
Tan E = 0.7251
E = 𝒕𝒂𝒏−𝟏𝟎. 𝟕𝟐𝟓𝟏
E = 35.95 °

5. MOTIVATION
02
It’s story time!

6. The Trigonometric River
Your loved one lives on the other side of the river.
Due to strict border protocol brought by pandemic,
you cannot see each other just yet. You decided to
send her a love letter through email. Because she’s
an avid trigonometric fan, you wanted to impress
her by applying trigonometry in your love letter.
Thus, you wanted to solve the width of the river
that separates you from her.

7. Let us Illustrate…
On your side of the bank, you
found a log that is 5 meters long,
then using your protractor, you
found that the angle between the
end of the log and her side of the
bank is 75° (as shown in the
figure).
Now solve for x which is the
width of the river. 5 meters
75°
x

8. Let us Process…
1 2
3 4
How will you solve for
the width of the river?
Is solving right triangles
useful in everyday life?
Were you able to apply the
trigonometric ratios in
solving for x in the right
triangle? How?
You are ready for
today’s lesson!

9. PRESENTATION OF THE LESSON
03
And the learning begins…

10. —M9GE-Ive-1
At the end of the lesson, the students shall be
able to use the trigonometric ratios to solve
real-life problems involving right triangles.
OBJECTIVE:

11. ACTIVITIES
04
A picture is worth a thousand words.

12. Solve for the width of the river.
5 m
x
75°
Solution:
tan 𝜃 =
𝑜𝑝𝑝
𝑎𝑑𝑗
tan 75° =
𝑥
5
5 tan 75° = 𝑥
5 3.7321 = 𝑥
𝒙 = 𝟏𝟖. 𝟔𝟔
The width of the river is
18.66 meters.

13. Find the distance between the
rock and the tower.
20 m
x
31°
Solution:
tan 𝜃 =
𝑜𝑝𝑝
𝑎𝑑𝑗
tan 31° =
20
𝑥
𝑥 =
20
tan 31°
𝑥 =
20
0.6009
𝒙 = 𝟑𝟑. 𝟐𝟖
The distance between the rock and the tower
is 33.28 meters.

14. Solve for ∠𝑨.
4 m
𝐴
Solution:
tan 𝐴 =
𝑜𝑝𝑝
𝑎𝑑𝑗
tan 𝐴 =
4
7
tan 𝐴 = 0.5714
𝐴 = 𝑡𝑎𝑛−10.5714
𝑨 = 𝟐𝟗. 𝟕𝟒
The measure of ∠𝑨 is 29.74°
7 m

15. Let’s Level Up!

16. Draw and Solve!
A ladder 6 meters long leans
against the wall of a building. If the
foot of the ladder makes an angle of
54° with the ground, how far is the
base of the ladder from the wall?

17. Draw and Solve!
A 5-meter ladder leans against the
wall of a house. The foot of the
ladder on the ground is 2.6 meters
from the wall. What angle does the
ladder make with the wall?

18. Draw and Solve!
A girl who is on the second floor of their
house watches her cat lying on the
ground. The angle between her eye level
and her line of sight is 36°. If the girl is
3 meters above the ground,
approximately how far is the cat from the
house?

19. ANALYSIS
05
Let’s see what you think!

20. Let’s answer these questions:
How important is
illustrating pictures
in solving word
problems involving
right triangles?
How did you use your
knowledge on
trigonometric ratios
in solving problems
involving right
triangles?

21. ABSTRACTION
06
I Knew It!

22. What are the steps in solving
real-life problems involving right
triangles?

23. Steps in solving real-life problems involving right triangles:
1 2
3 4
Draw and label.
Determine the formula
(trigonometric ratio) to
be used.
Identify what are given
and what is asked in the
problem (opposite,
adjacent or hypotenuse).
Solve.

24. APPLICATION
07
Let’s Do This!

25. The Exodus Problem
From point A, Moses walked
65 miles west then 58 miles
north to his destination B. Find
the angles made from his
starting point to his destination
and vice versa (∠𝐴 and ∠𝐵)
and his displacement (c).
A
B
c
C

26. EVALUATION
08
Test Is It!

27. Illustrate the following problems then solve.
1. A ladder 6 meters long leans against the wall of a house. If the foot of the ladder makes
an angle of 65° with the ground, how far is the base of the ladder from the wall?
2. Drake is flying a kite. He is holding the end of the string at a distance of 1.5 m above the
ground. If the string is 18 m long and makes an angle of 42° with the horizontal, how high
is the kite above the ground?
3. A 10-meter post was unearthed and leaned on the tree. The foot of the post is 4.6
meters from the base of the tree. What angle does the post make with the tree?

28. CREDITS: This presentation template was
created by Slidesgo, including icons by Flaticon
and infographics & images by Freepik.
THANKS
Do you have any questions?
diazrheaann@gmail.com
+63919 966 7417
Please keep this slide for attribution.