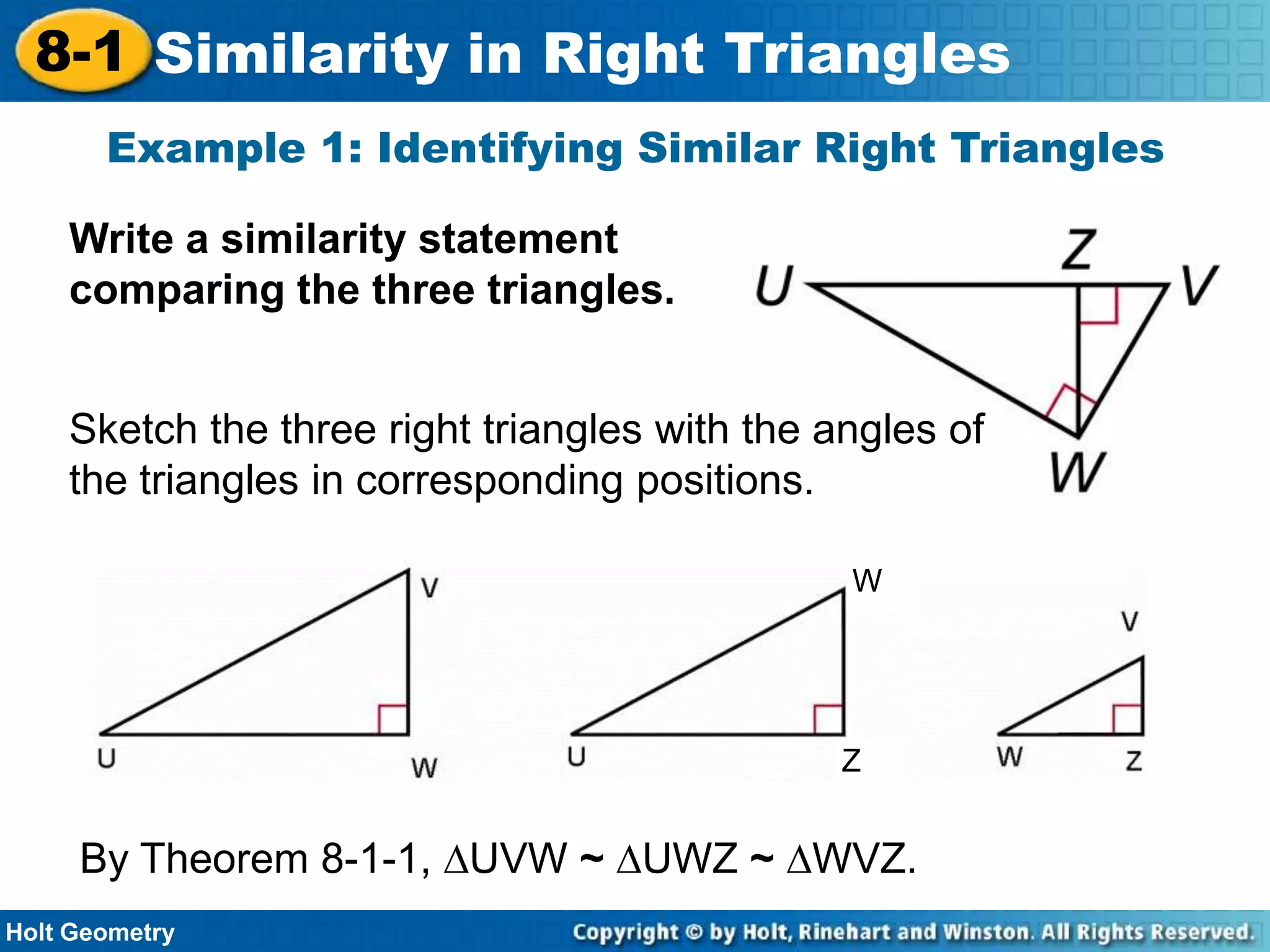
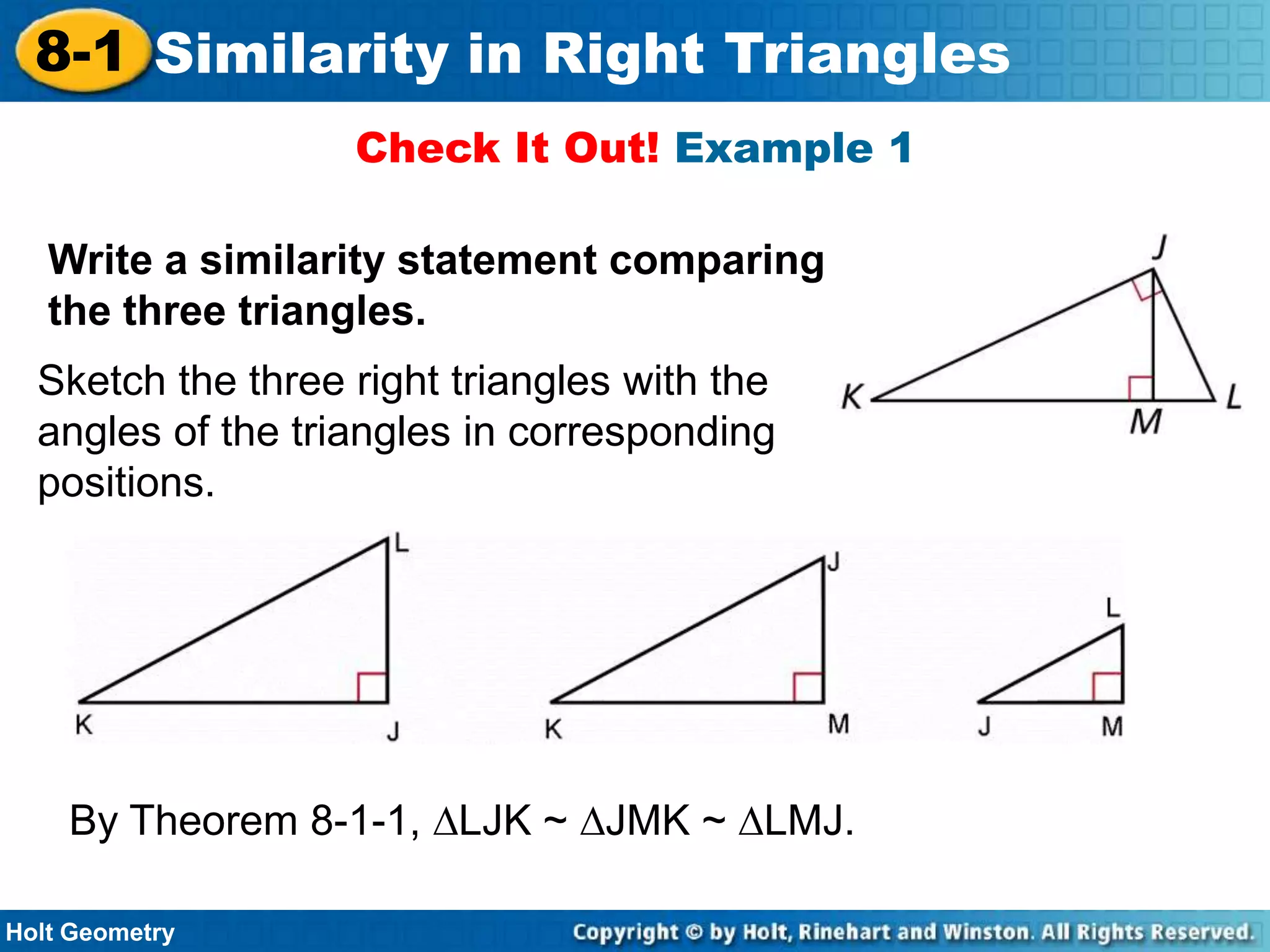
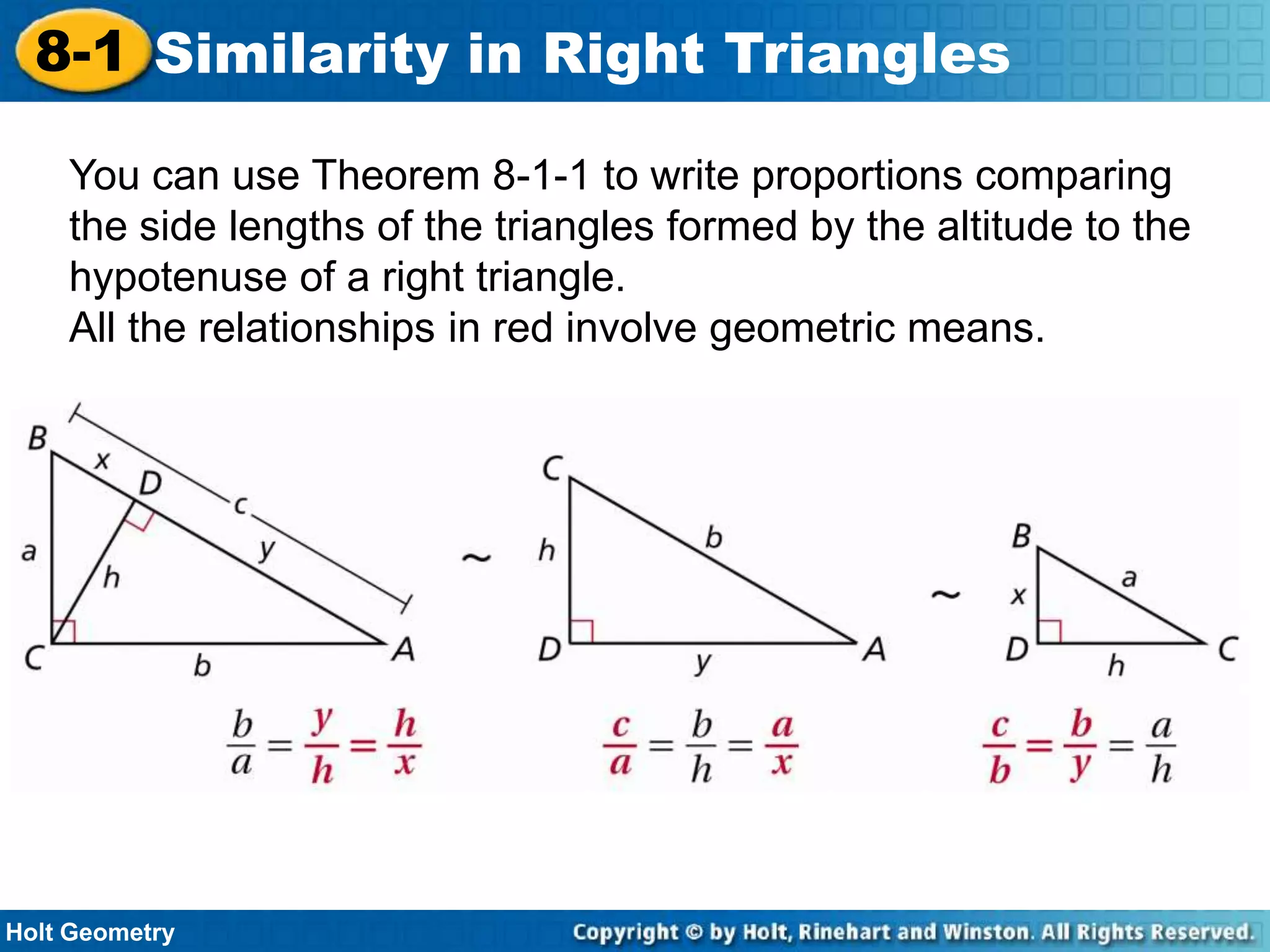
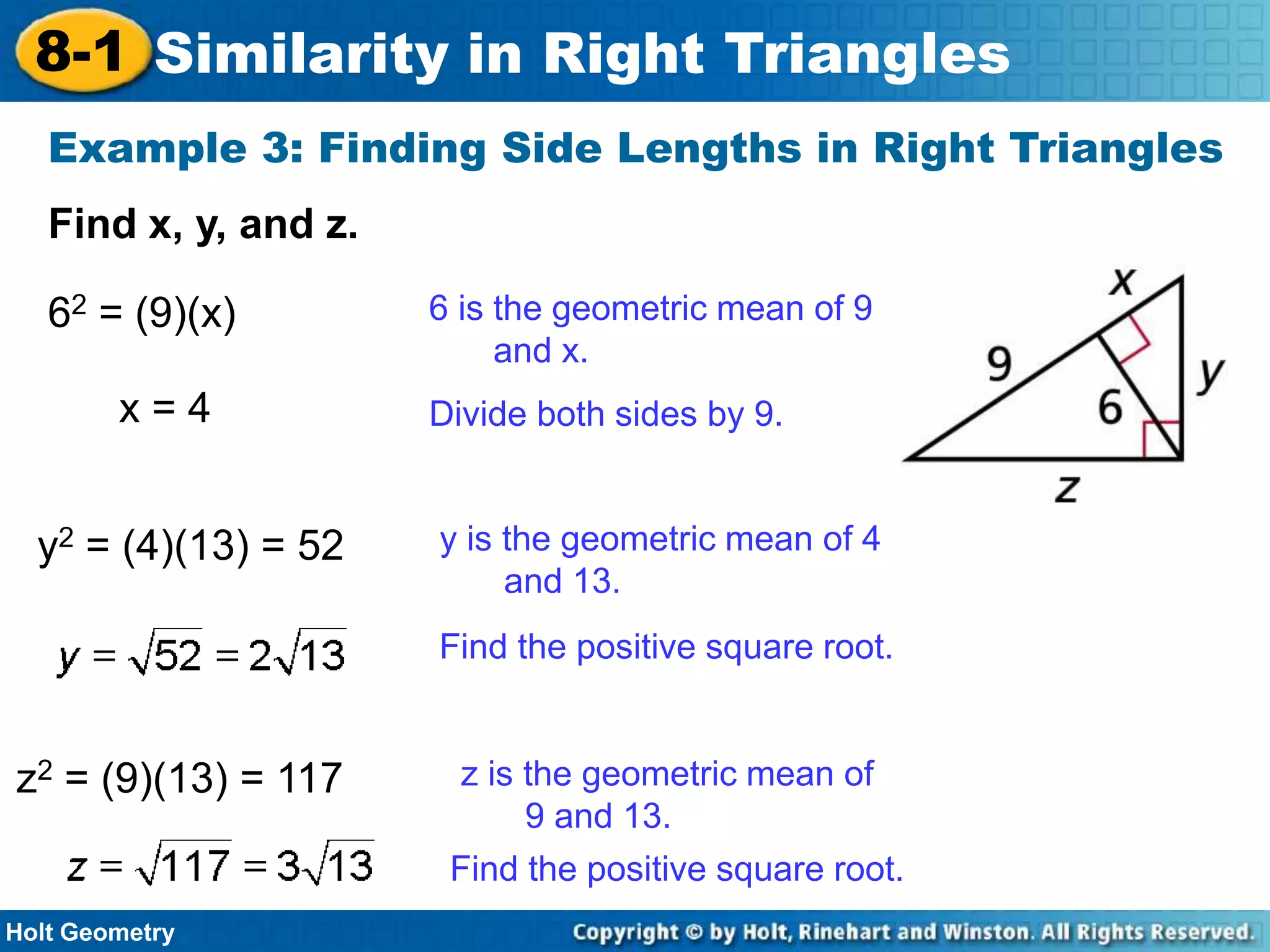
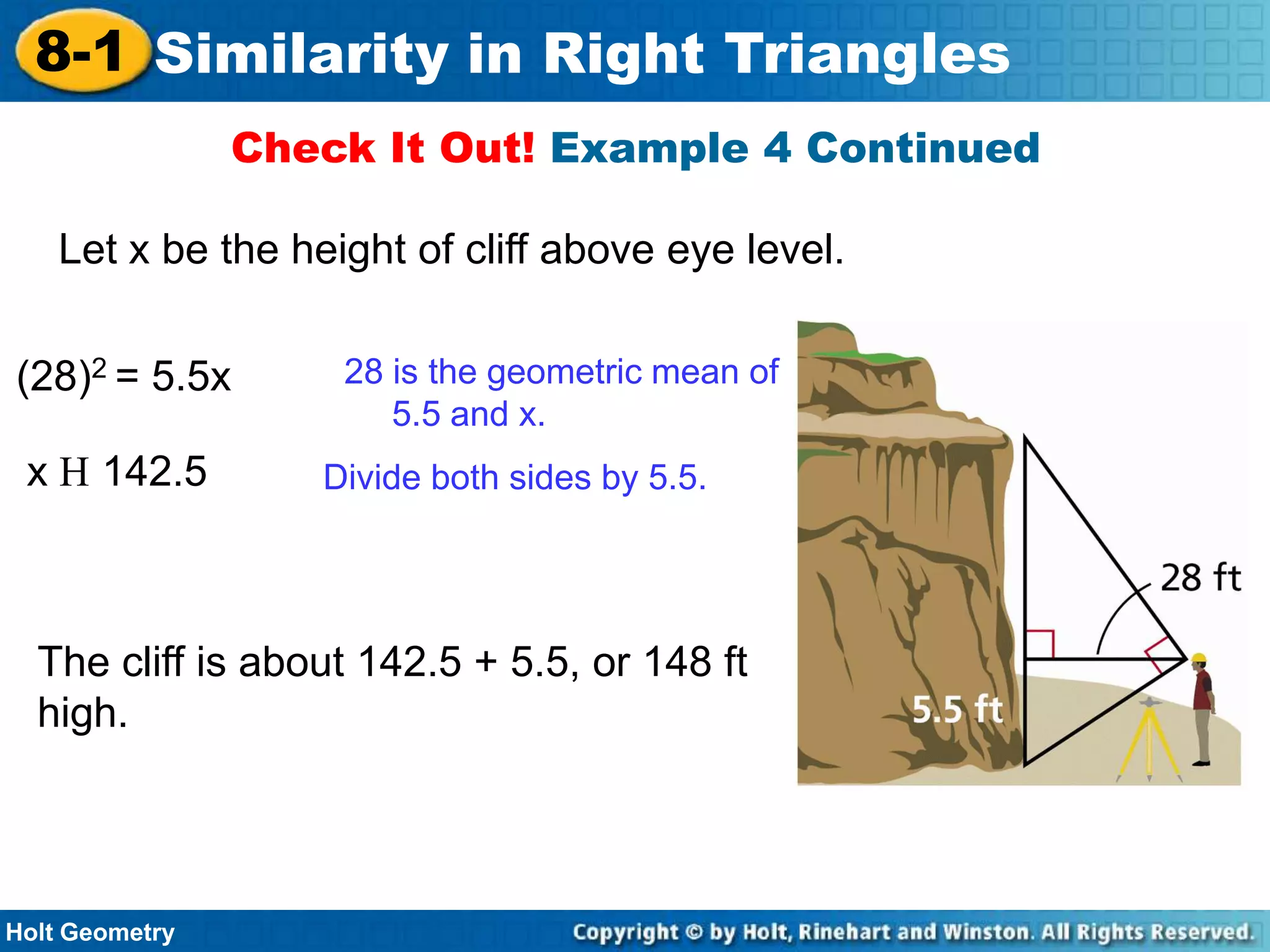
This document provides instruction on similarity in right triangles. It begins with examples of identifying similar right triangles and finding geometric means. Geometric mean is defined as the positive square root of the product of two numbers. The document then shows how geometric means can be used to find unknown side lengths in right triangles using proportions. Examples demonstrate applications to measurement problems. The lesson concludes with a quiz reviewing key concepts like writing similarity statements and using proportions with geometric means to solve for missing side lengths in right triangles.

1. 8-1 Similarity in Right Triangles
8-1 Similarity in Right Triangles
Warm Up
Lesson Presentation
Lesson Quiz
Holt Geometry
Holt Geometry

2. 8-1 Similarity in Right Triangles
Warm Up
1. Write a similarity statement
comparing the two triangles.
∆ADB ~ ∆EDC
Simplify.
2.
3.
Solve each equation.
4.
Holt Geometry
5. 2x2 = 50
±5

3. 8-1 Similarity in Right Triangles
Objectives
Use geometric mean to find segment lengths
in right triangles.
Apply similarity relationships in right triangles
to solve problems.
Holt Geometry

4. 8-1 Similarity in Right Triangles
Vocabulary
geometric mean
Holt Geometry

5. 8-1 Similarity in Right Triangles
In a right triangle, an altitude drawn from the vertex of the
right angle to the hypotenuse forms two right triangles.
Holt Geometry

6. 8-1 Similarity in Right Triangles
Holt Geometry

7. 8-1 Similarity in Right Triangles
Example 1: Identifying Similar Right Triangles
Write a similarity statement
comparing the three triangles.
Sketch the three right triangles with the angles of
the triangles in corresponding positions.
W
Z
By Theorem 8-1-1, ∆UVW ~ ∆UWZ ~ ∆WVZ.
Holt Geometry

8. 8-1 Similarity in Right Triangles
Check It Out! Example 1
Write a similarity statement comparing
the three triangles.
Sketch the three right triangles with the
angles of the triangles in corresponding
positions.
By Theorem 8-1-1, ∆LJK ~ ∆JMK ~ ∆LMJ.
Holt Geometry

9. 8-1 Similarity in Right Triangles
Consider the proportion
. In this case, the
means of the proportion are the same number, and
that number is the geometric mean of the extremes.
The geometric mean of two positive numbers is the positive
square root of their product. So the geometric mean of a and b is
the positive number x such
that
Holt Geometry
, or x2 = ab.

10. 8-1 Similarity in Right Triangles
Example 2A: Finding Geometric Means
Find the geometric mean of each pair of numbers. If
necessary, give the answer in simplest radical form.
4 and 25
Let x be the geometric mean.
x2 = (4)(25) = 100
x = 10
Holt Geometry
Def. of geometric mean
Find the positive square root.

11. 8-1 Similarity in Right Triangles
Example 2B: Finding Geometric Means
Find the geometric mean of each pair of numbers. If
necessary, give the answer in simplest radical form.
5 and 30
Let x be the geometric mean.
x2 = (5)(30) = 150
Def. of geometric mean
Find the positive square root.
Holt Geometry

12. 8-1 Similarity in Right Triangles
Check It Out! Example 2a
Find the geometric mean of each pair of numbers. If
necessary, give the answer in simplest radical form.
2 and 8
Let x be the geometric mean.
x2 = (2)(8) = 16
x=4
Holt Geometry
Def. of geometric mean
Find the positive square root.

13. 8-1 Similarity in Right Triangles
Check It Out! Example 2b
Find the geometric mean of each pair of numbers. If
necessary, give the answer in simplest radical form.
10 and 30
Let x be the geometric mean.
x2 = (10)(30) = 300
Def. of geometric mean
Find the positive square root.
Holt Geometry

14. 8-1 Similarity in Right Triangles
Check It Out! Example 2c
Find the geometric mean of each pair of numbers. If
necessary, give the answer in simplest radical form.
8 and 9
Let x be the geometric mean.
x2 = (8)(9) = 72
Def. of geometric mean
Find the positive square root.
Holt Geometry

15. 8-1 Similarity in Right Triangles
You can use Theorem 8-1-1 to write proportions comparing
the side lengths of the triangles formed by the altitude to the
hypotenuse of a right triangle.
All the relationships in red involve geometric means.
Holt Geometry

16. 8-1 Similarity in Right Triangles
Holt Geometry

17. 8-1 Similarity in Right Triangles
Example 3: Finding Side Lengths in Right Triangles
Find x, y, and z.
62 = (9)(x)
x=4
y2 = (4)(13) = 52
6 is the geometric mean of 9
and x.
Divide both sides by 9.
y is the geometric mean of 4
and 13.
Find the positive square root.
z2 = (9)(13) = 117
Holt Geometry
z is the geometric mean of
9 and 13.
Find the positive square root.

18. 8-1 Similarity in Right Triangles
Helpful Hint
Once you’ve found the unknown side lengths, you can
use the Pythagorean Theorem to check your answers.
Holt Geometry

19. 8-1 Similarity in Right Triangles
Check It Out! Example 3
Find u, v, and w.
92 = (3)(u)
9 is the geometric mean of
u and 3.
u = 27
Divide both sides by 3.
w2 = (27 + 3)(27) w is the geometric mean of
u + 3 and 27.
Find the positive square root.
v2 = (27 + 3)(3)
Holt Geometry
v is the geometric mean of
u + 3 and 3.
Find the positive square root.

20. 8-1 Similarity in Right Triangles
Example 4: Measurement Application
To estimate the height of a
Douglas fir, Jan positions herself
so that her lines of sight to the
top and bottom of the tree form a
90º angle. Her eyes are about 1.6
m above the ground, and she is
standing 7.8 m from the tree.
What is the height of the tree to
the nearest meter?
Holt Geometry

21. 8-1 Similarity in Right Triangles
Example 4 Continued
Let x be the height of the tree above eye level.
(7.8)2 = 1.6x
x = 38.025 ≈ 38
7.8 is the geometric mean of
1.6 and x.
Solve for x and round.
The tree is about 38 + 1.6 = 39.6, or 40 m tall.
Holt Geometry

22. 8-1 Similarity in Right Triangles
Check It Out! Example 4
A surveyor positions himself so
that his line of sight to the top of a
cliff and his line of sight to the
bottom form a right angle as
shown.
What is the height of the cliff to
the nearest foot?
Holt Geometry

23. 8-1 Similarity in Right Triangles
Check It Out! Example 4 Continued
Let x be the height of cliff above eye level.
(28)2 = 5.5x
x
142.5
28 is the geometric mean of
5.5 and x.
Divide both sides by 5.5.
The cliff is about 142.5 + 5.5, or 148 ft
high.
Holt Geometry

24. 8-1 Similarity in Right Triangles
Lesson Quiz: Part I
Find the geometric mean of each pair of numbers. If
necessary, give the answer in simplest radical form.
1. 8 and 18
2. 6 and 15
Holt Geometry
12

25. 8-1 Similarity in Right Triangles
Lesson Quiz: Part II
For Items 3–6, use ∆RST.
3. Write a similarity statement comparing the three
triangles.
∆RST ~ ∆RPS ~ ∆SPT
4. If PS = 6 and PT = 9, find PR.
4
5. If TP = 24 and PR = 6, find RS.
6. Complete the equation (ST)2 = (TP + PR)(?).
Holt Geometry
TP