This document provides examples and steps for solving various types of equations beyond linear equations, including:
1) Polynomial equations solved by factoring
2) Equations with radicals where radicals are eliminated by raising both sides to a power
3) Equations with rational exponents where both sides are raised to the reciprocal power
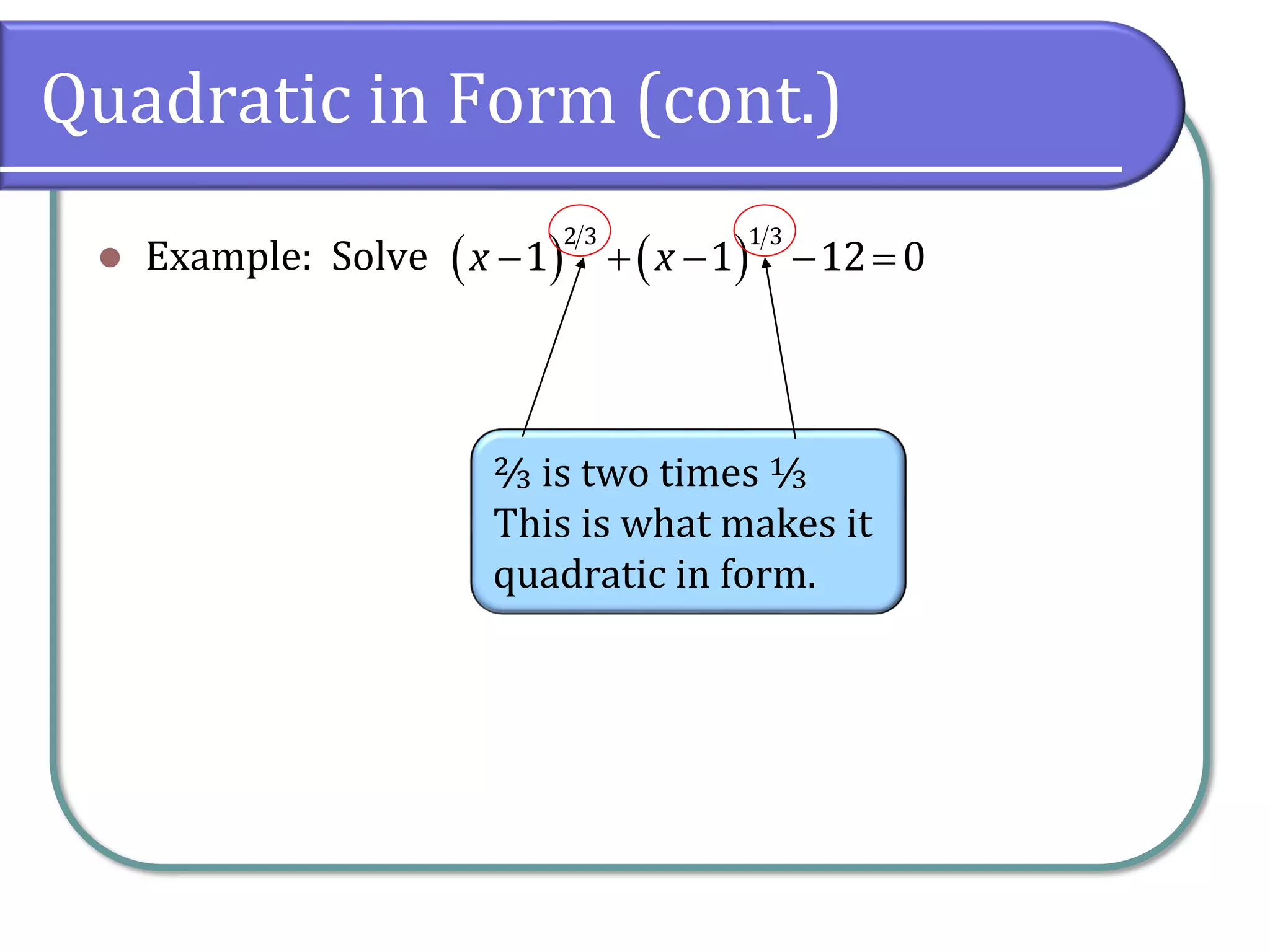
4) Equations quadratic in form where an algebraic substitution is made to transform into a quadratic equation
5) Absolute value equations where both positive and negative solutions must be considered.