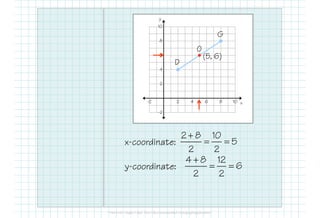
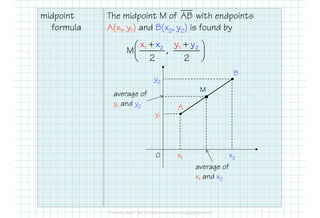
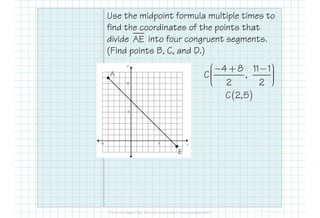
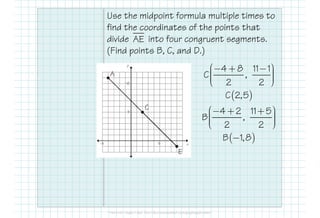
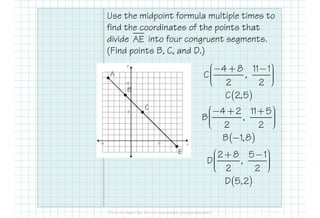
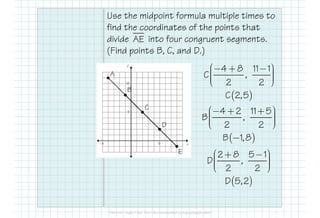
This document provides formulas and examples for finding midpoints and partitions of line segments in geometry. It illustrates how to calculate midpoints between two points, find endpoint coordinates given a midpoint, and determine points that divide a segment into specific ratios. Key formulas and example problems facilitate understanding of these concepts.

1. Midpoint and Partition Formulas
The student will be able to (I can):
• Find the midpoint of two given points.
• Find the coordinates of an endpoint given one endpoint
and a midpoint.and a midpoint.
• Find the coordinates of a point a fractional distance from
one end of a segment.

2. The coordinates of a midpoint are the
averages of the coordinates of the
endpoints of the segment.
C A T
1 3 2
1
2 2
− +
= =

3. -2 2 4 6 8 10
2
4
6
8
10
x
y
• (5, 6)
D
O
G
-2
x-coordinate:
y-coordinate:
2 8 10
5
2 2
+
= =
4 8 12
6
2 2
+
= =

4. midpoint
formula
The midpoint M of with endpoints
A(x1, y1) and B(x2, y2) is found by
AB
1 12 2
M ,
2 2
yxx y+ + 
 
 
A
B
y
y2
●
M
average of
y1 and y2
0
A
x1 x2
y1
average of
x1 and x2

5. Example Find the midpoint of QR for Q(—3, 6) and
R(7, —4)
x1 y1 x2 y2
Q(—3, 6) R(7, —4)
21x 3x 7 4
2
2 2 2
+ +
= = =
−
21 2
1
yy 6 4+ +
=
−
= =21 2
1
y
2 2
y 6
2
4+ +
=
−
= =
M(2, 1)

6. Problems 1. What is the midpoint of the segment
joining (8, 3) and (2, 7)?
A. (10, 10)
B. (5, —2)
C. (5, 5)
D. (4, 1.5)
8 2 10
5
2 2
+
= =
3 7 10
5
2 2
+
= =

7. Problems 2. What is the midpoint of the segment
joining (—4, 2) and (6, —8)?
A. (—5, 5)
B. (1, —3)
C. (2, —6)
D. (—1, 3)
4 6 2
1
2 2
− +
= =

8. Problem 3. Point M(7, —1) is the midpoint of ,
where A is at (14, 4). Find the
coordinates of point B.
A. (7, 2)
B. (—14, —4)
C. (0, —6)
D. (10.5, 1.5)
AB
D. (10.5, 1.5)
14 7 7− = 7 7 0− =
( )4 1 5− − = 1 5 6− − = −

9. Use the midpoint formula multiple times to
find the coordinates of the points that
divide into four congruent segments.
(Find points B, C, and D.)
AE
A
4 8 11 1
C ,
2 2
 − + −    
( )C 2,5
E

10. Use the midpoint formula multiple times to
find the coordinates of the points that
divide into four congruent segments.
(Find points B, C, and D.)
AE
A
4 8 11 1
C ,
2 2
 − + −    
( )C 2,5
C
4 2 11 5 − + + 
E
C
4 2 11 5
B ,
2 2
 − + +    
( )B 1,8−

11. Use the midpoint formula multiple times to
find the coordinates of the points that
divide into four congruent segments.
(Find points B, C, and D.)
AE
A
4 8 11 1
C ,
2 2
 − + −    
( )C 2,5
C
4 2 11 5 − + + 
B
E
C
4 2 11 5
B ,
2 2
 − + +    
( )B 1,8−
2 8 5 1
D ,
2 2
 + −    
( )D 5,2

12. Use the midpoint formula multiple times to
find the coordinates of the points that
divide into four congruent segments.
(Find points B, C, and D.)
AE
A
4 8 11 1
C ,
2 2
 − + −    
( )C 2,5
C
4 2 11 5 − + + 
B
E
C
4 2 11 5
B ,
2 2
 − + +    
( )B 1,8−
2 8 5 1
D ,
2 2
 + −    
( )D 5,2
D

13. partitioning a
segment
Dividing a segment into two pieces whose
lengths fit a given ratio.
For a line segment with endpoints (x1, y1)
and (x2, y2), to partition in the ratio b: a,
Example: has endpoints A(—3, —16)AB
1 2 1 2ax bx ay by
,
a b a b
 + +    + +
Example: has endpoints A(—3, —16)
and B(15, —4). Find the
coordinates of P that partition
the segment in the ratio 1 : 2.
AB
( ) ( ) ( ) ( )2 3 1 15 2 16 1 4
P ,
1 2 1 2
 − + − + −    + + 
( )P 3, 12−