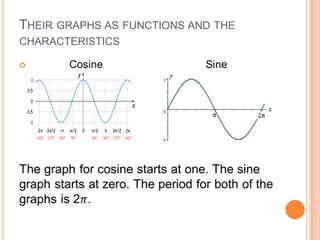
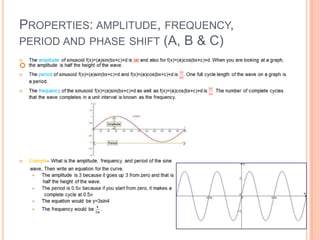
This document outlines a trigonometry curriculum across 4 units: Unit 1 covers measuring angles in degrees and radians, converting between the two systems, graphing trig functions, and using trig functions to solve right triangles. Unit 2 covers trig functions of the form f(t)=A sin (Bt + C) and f(t)=A cos (Bt + C), their properties including amplitude, frequency, period and phase shift, and using trig functions to solve word problems. Unit 3 covers analytical trigonometry including fundamental identities, Pythagorean identities, sum and difference formulas, and using double-angle and half-angle formulas. It also covers the law of sines and cosines.

1. UNIT 1
 Angles
 4.1
 Sine and cosine
 4.2, 4.3, 4.8

2. HOW TO MEASURE IN BOTH DEGREES AND
RADIANS
 A degree is a measurement you use in angles. One
way that you can get an angle is using sine, cosine,
or tangent inverse.
 A radian is when the measure is 1 radian for the
central angle of a circle if it shows an arc with the
same length like the radius.

3. KNOW THE CONVERSION BETWEEN DEGREES
AND RADIAN MEASURE
 To convert radians to degrees, you have to multiply
180÷π radians
 Example- 3 π rad × 180° (3/4)×180= 135°
4 π rad
 To convert degrees to radians, you must multiply π
radians÷180
 Example- 60° × π rad =60 π rad= π/3 rad
1 180° 180°

4. THEIR GRAPHS AS FUNCTIONS AND THE
CHARACTERISTICS


5. THEIR DEFINITION AS X- & Y-COORDINATES ON
THE UNIT CIRCLE
 Sine=y
 Cosine=x
 Example: 5π/6 is equal to 150° and the point is
(-√3/2,1/2)
 Sine would equal 1/2 , while cosine equals -√3/2

6. STUDENTS ARE CAPABLE OF COMPUTING UNKNOWN
SIDES OR ANGLES IN A RIGHT TRIANGLE.
 In order to find a side of a right triangle you can use the Pythagorean
Theorem, which is a^2+b^2=c^2. The a and b represent the two shorter sides
and the c represents the longest side which is the hypotenuse.
 Example- if you have to sides with the measurement of 3 and 5 and you
are trying to fine the hypotenuse then you would use the formula
3^2+5^2=c^2 . You will get 9+25=c^2 and then 34=c^2 and you would
have to square both sides and you get the hypotenuse (c)
 To get the angle of a right angle you can use sine, cosine, and tangent
inverse. They are expressed as tan^(-1) ,cos^(-1) , and sin^(-1) .
 Example- if you want to fine the angle across from three on the right
angle above then you would use tangent inverse. It would be tan A=3/5
and then you multiply both sides by tan^(-1) and you get tan^(-1) 〖
(3/5)〗. You put that in the calculator and you get side A.

7. STUDENTS USE TRIGONOMETRY IN A VARIETY
OF WORDS PROBLEMS.
 Example- “Suppose you are standing on one bank of a river. A
tree on the other side of the river is known to be 150 ft. tall. A
lone from the top of the tree to the ground at your feet makes
an angle of 11° with the ground. How far from you is he base
of the tree?”
(x)tan11°=150/x (x)
.19x/.19=150/.19 150 ft
x=789.47 ft. 11° x
Word problems are expressed to show real life situations. Word
problems are usually more difficult than a problem from the
actual lesson. The word problems we do are the same as the
problems we usually do but it just requires more thinking.

8. UNIT 2
 Functions of the form f(t)=A sin (Bt + C) &
f(t)=A cos (Bt + C):
 4.4, 4.5, 4.7, 4.8

9. PROPERTIES: AMPLITUDE, FREQUENCY,
PERIOD AND PHASE SHIFT (A, B & C)


10. STUDENT WILL BE ABLE TO TAKE A GIVEN ANGLE AND COMPUTE THE
TRIGONOMETRIC FUNCTION AND ITS INVERSE WITH THE AID OF THE UNIT
CIRCLE (BY HAND)


11. STUDENTS USE TRIGONOMETRY IN A VARIETY
OF WORD PROBLEMS.
 “When sitting atop a tree and looking down at his pal Joey, the angle
of depression of Mack’s line of sight is 38°32’. If joey is know to be
standing 39 feet from the base of the tree, how tall is the tree ?
h
39 ft 38°32’
 First you must convert the 32 into degrees so you divide
it by 60 and then add it to 38 and you get 38.5°.
 Then to get the height you have to use tangent and you
use tan38.5°=h/39 and you get the height of the tree to
be approximately 31 ft.

12. UNIT 3
 Analytical Trigonometry
 5.1, 5.2, 5.3, 5.4
 5.5, 5.6

13. FUNDAMENTAL IDENTITIES


14. PYTHAGOREAN IDENTITIES


15. SUM AND DIFFERENCE FORMULAS


16. USE DOUBLE-ANGLE AND HALF-ANGLE FORMULAS TO PROVE AND/OR
SIMPLIFY OTHER TRIGONOMETRIC IDENTITIES.


17. STUDENTS WILL BE FAMILIAR WITH THE LAW OF SINES
AND LAW OF COSINES TO SOLVE PROBLEMS


18. UNIT 4
 Applications of Trigonometry
 6.1, 6.2, 6.3, 6.4, 6.5

19. 
STUDENTS NEED TO KNOW HOW TO WRITE EQUATIONS IN
RECTANGULAR COORDINATES IN TERMS OF POLAR COORDINATES

20. VECTORS-MAGNITUDE


21. VECTORS-ADDITION AND SCALAR
MULTIPLICATION
 U=(u1,u2), v=(v1,v2) are vectors. When you are adding you
use the formula u+v=(u1+v1,u2,v2). K is known to be a real
number and you would use it to multiply with the formula
ku=k(u1,u2)=<ku1,ku2>.
 Example- let u=<-1,3> and v=<4,7> and add the vectors.
 u+v=(-1,3)+(4,7)=(-1+4,3+7) <-3,10>
 All you have to do is add the first number from each point
to get the x and add the second number from each point
together to get the y.
 Example- use scalar multiplication to find 3u when
u=<-1,3>.
 Since there is a 3 before the u, you have to multiply each
number in the point by three.
 3u=3(-1,3)=(-3,9)

22. VECTORS-RESOLVING THE VECTOR
 The formula v=(|v|cosƟ,|v|sinƟ) can be used when v has a
direction angle Ɵ and the components of v can be calculated.
The unit vector in the direction of v is u=v/|v|=(cosƟ,sinƟ).
 Example- “find the components of vector v with direction angle
115 and magnitude 6.”
 All you have to do is substitute 6 which is the magnitude
into the equation wherever there is a v. Also plug in 115
wherever there is a Ɵ.
 V=(a,b)=(6cos115 ,6sin115 )  a would be approximately -
2.54 while b would be about 5.44

23. VECTORS-DOT PRODUCT


24. VECTORS-ANGLE BETWEEN TWO VECTORS


25. PARAMETRIC RELATIONS

x y t
-6 -6 -3
-1 -4 -2
2 -2 -1
3 0 0
2 2 1
-1 4 2
-6 6 3