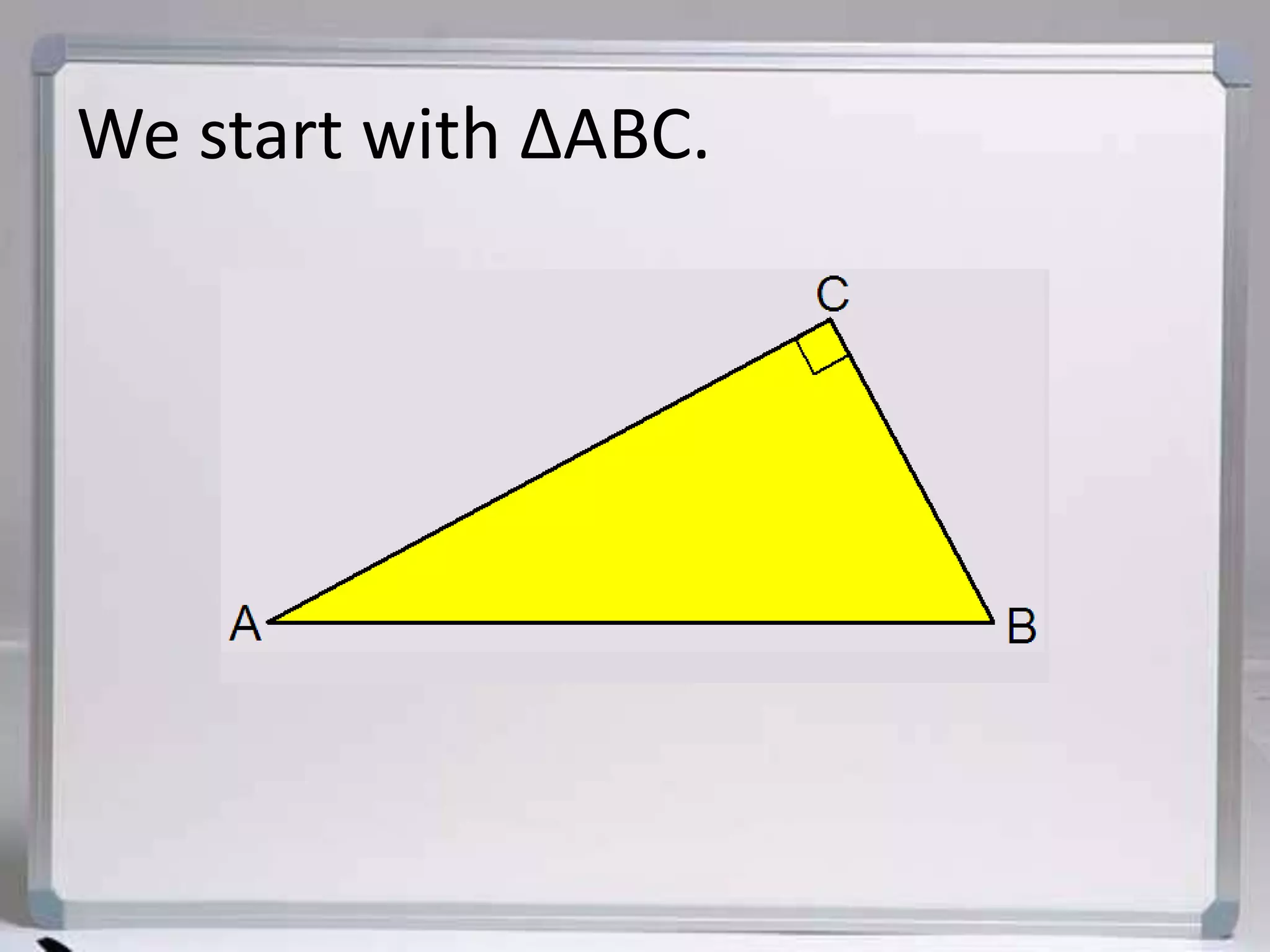
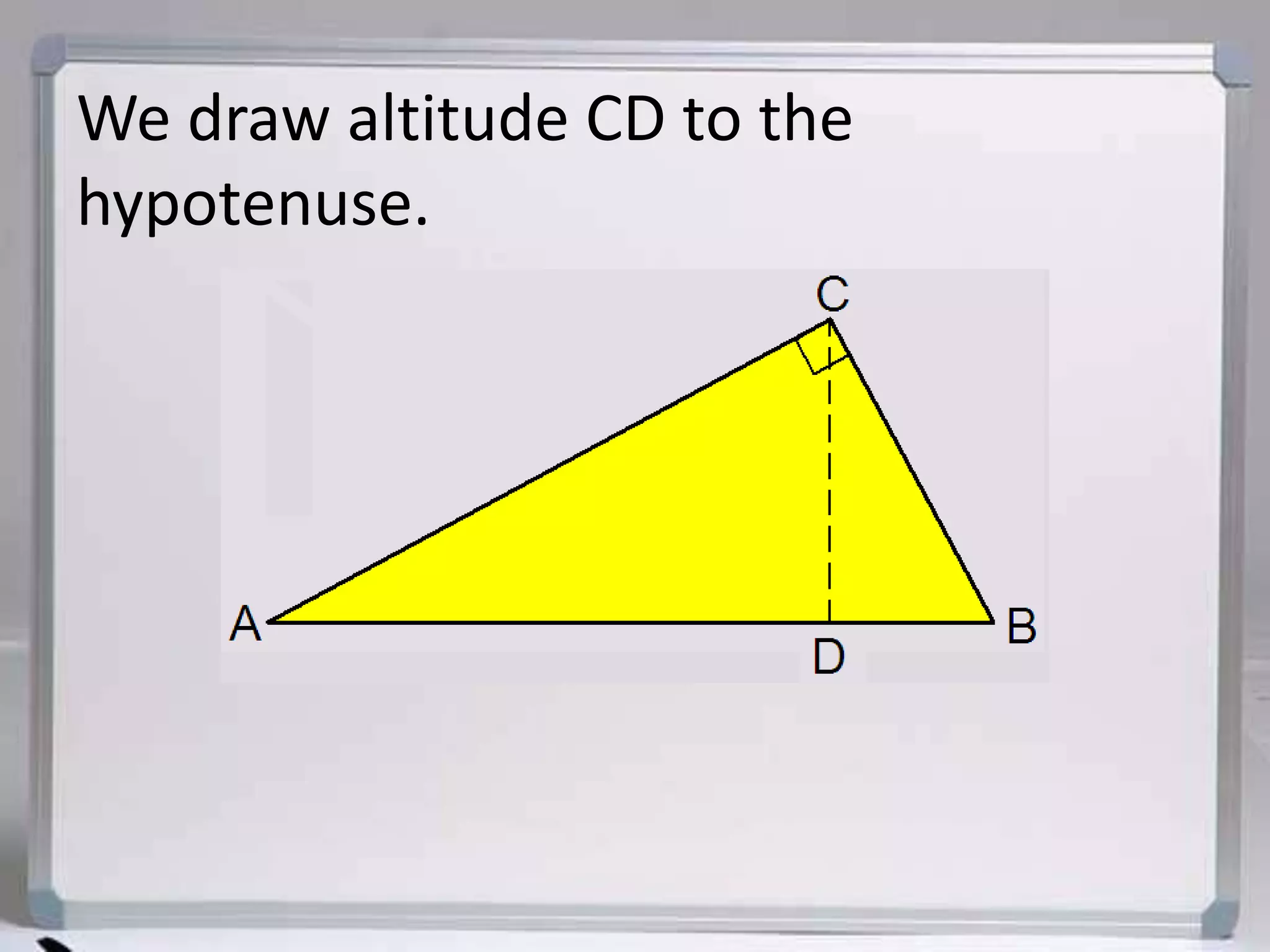
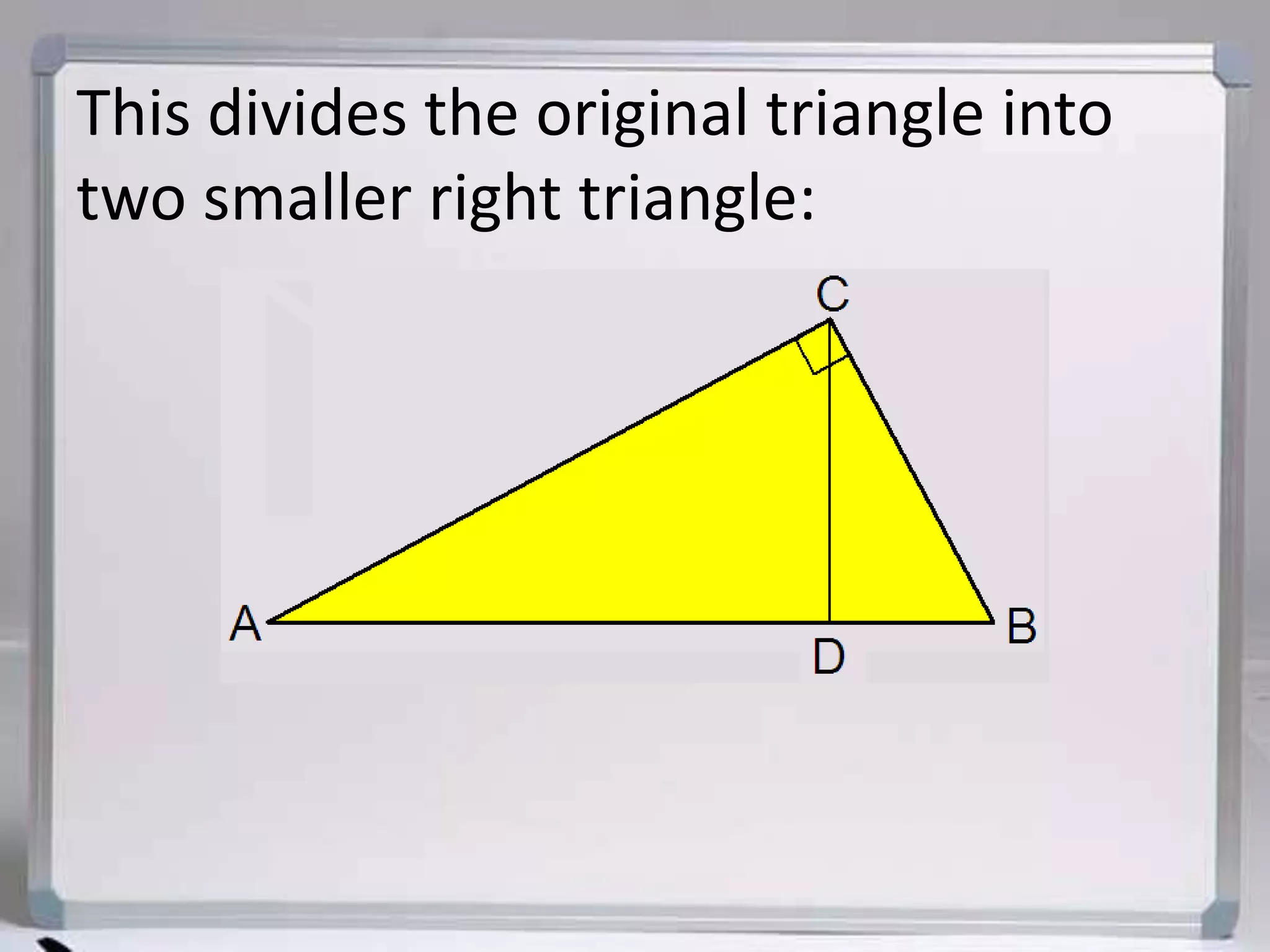
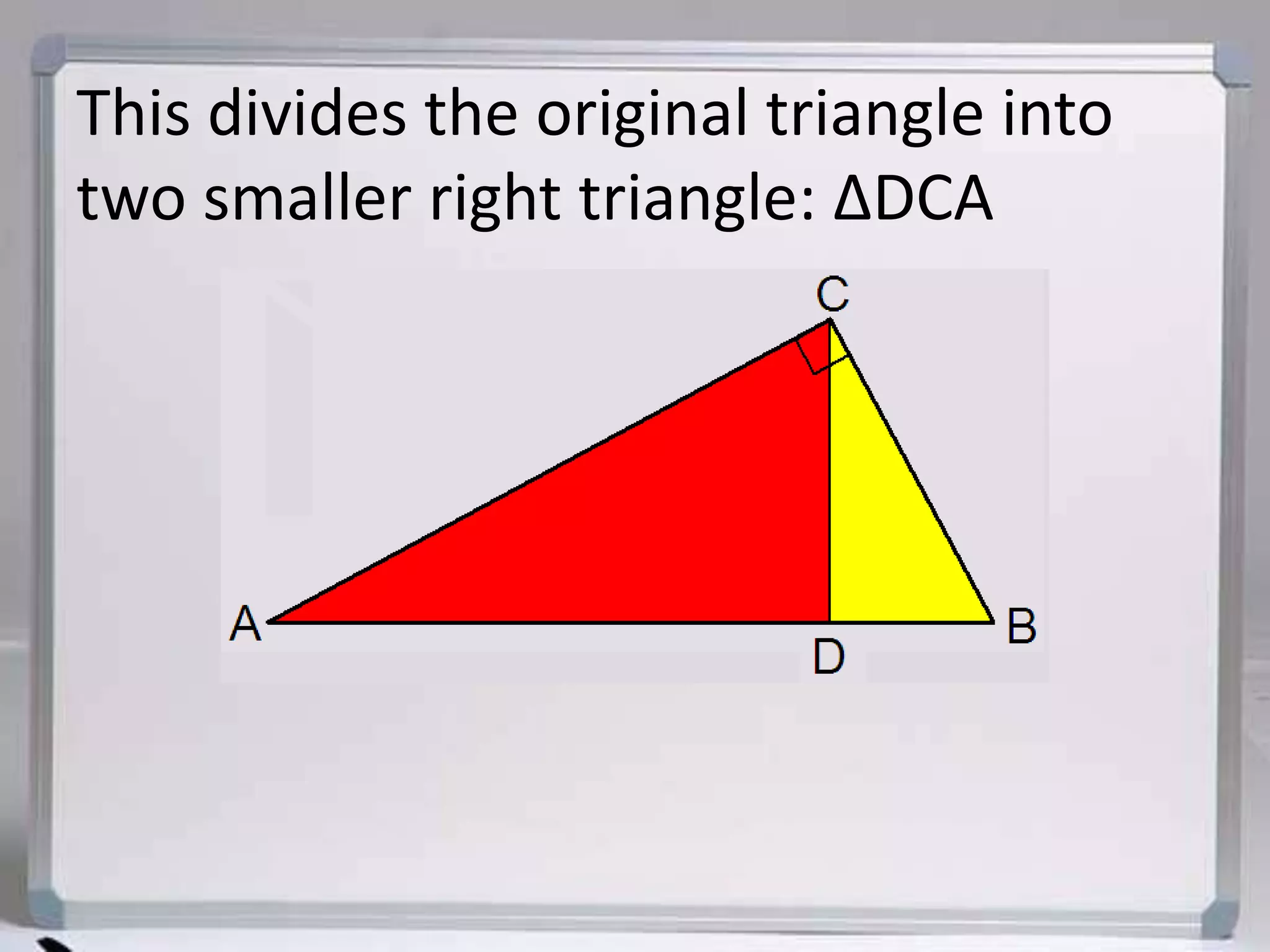
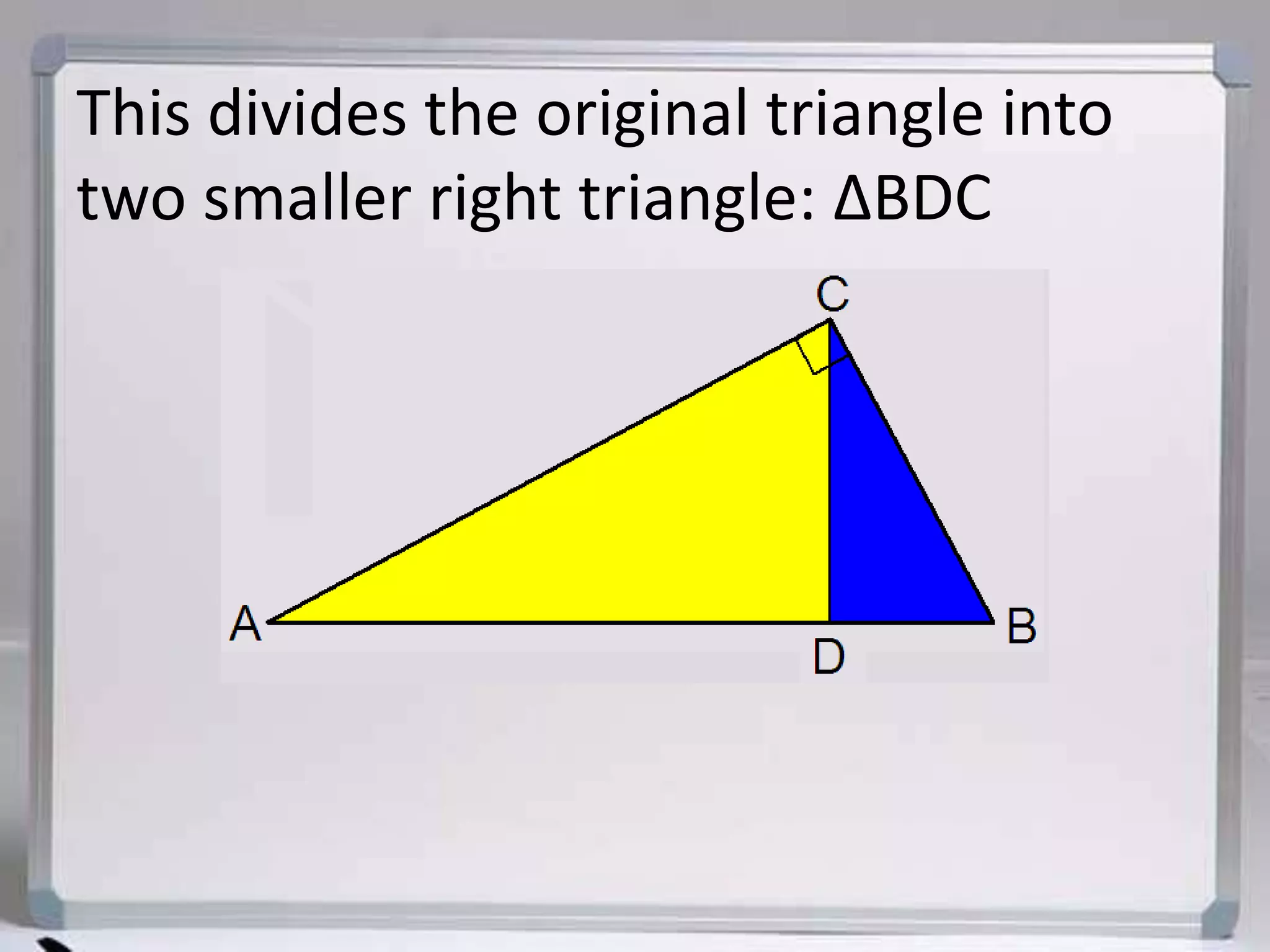
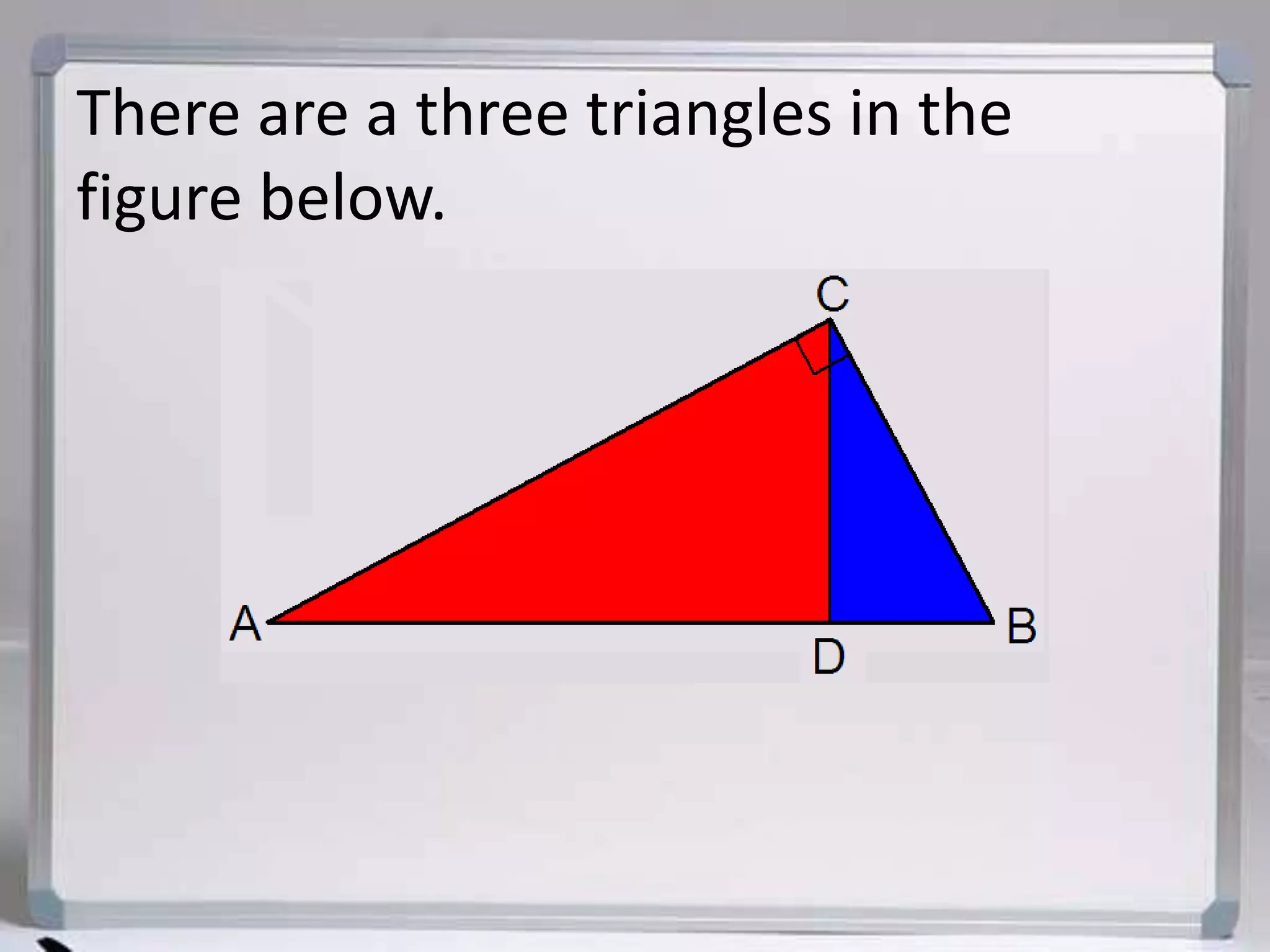
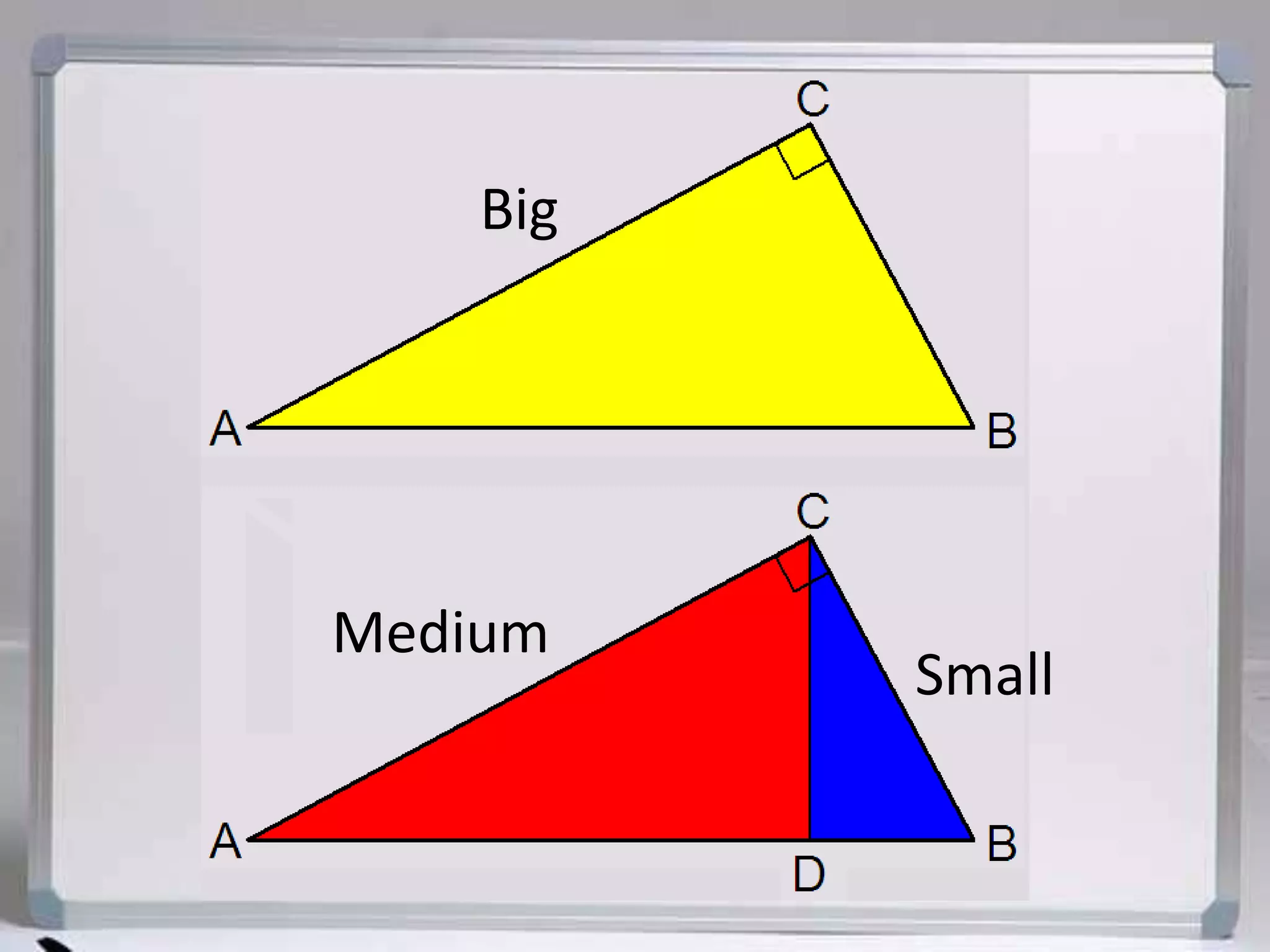
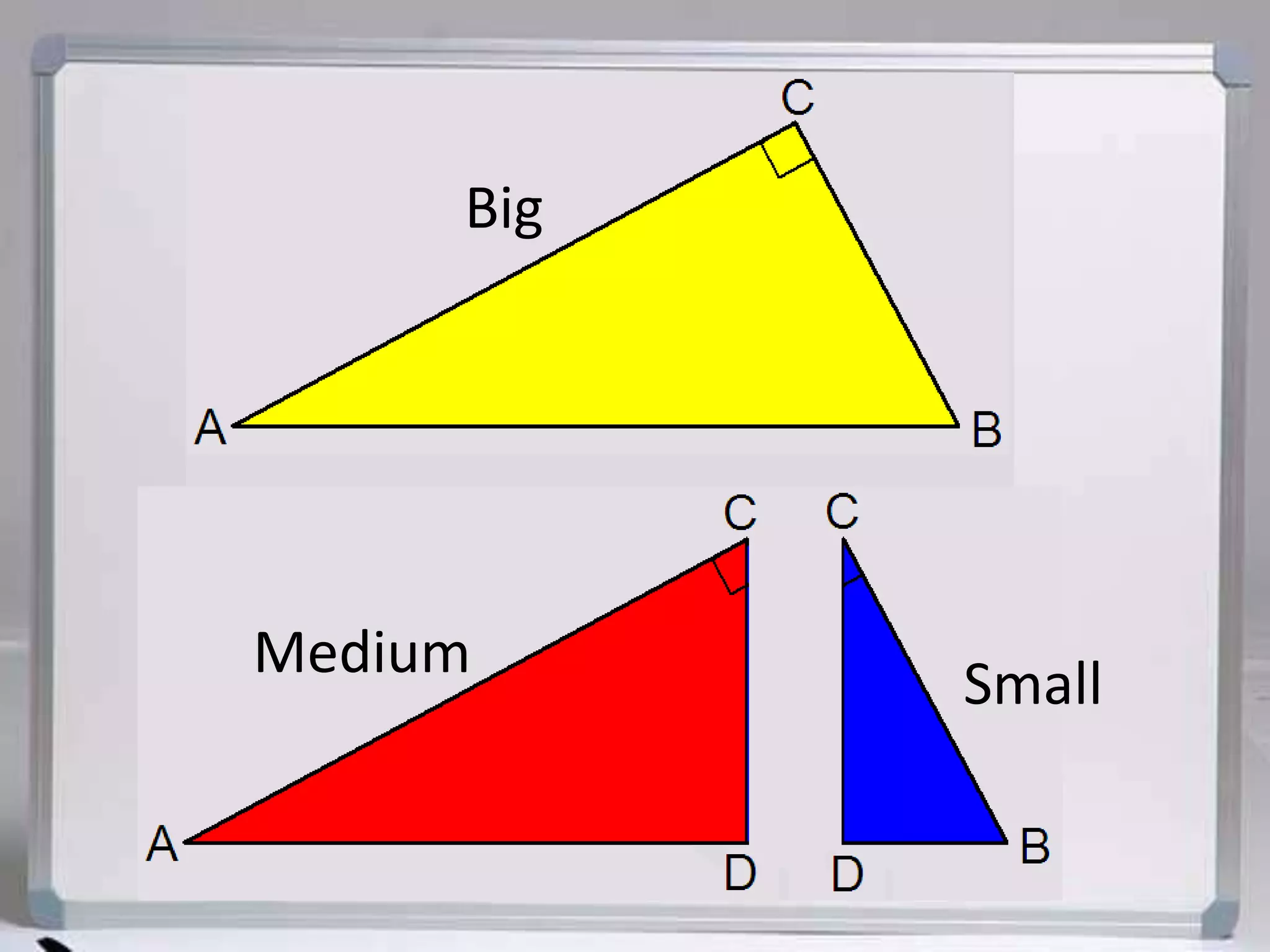
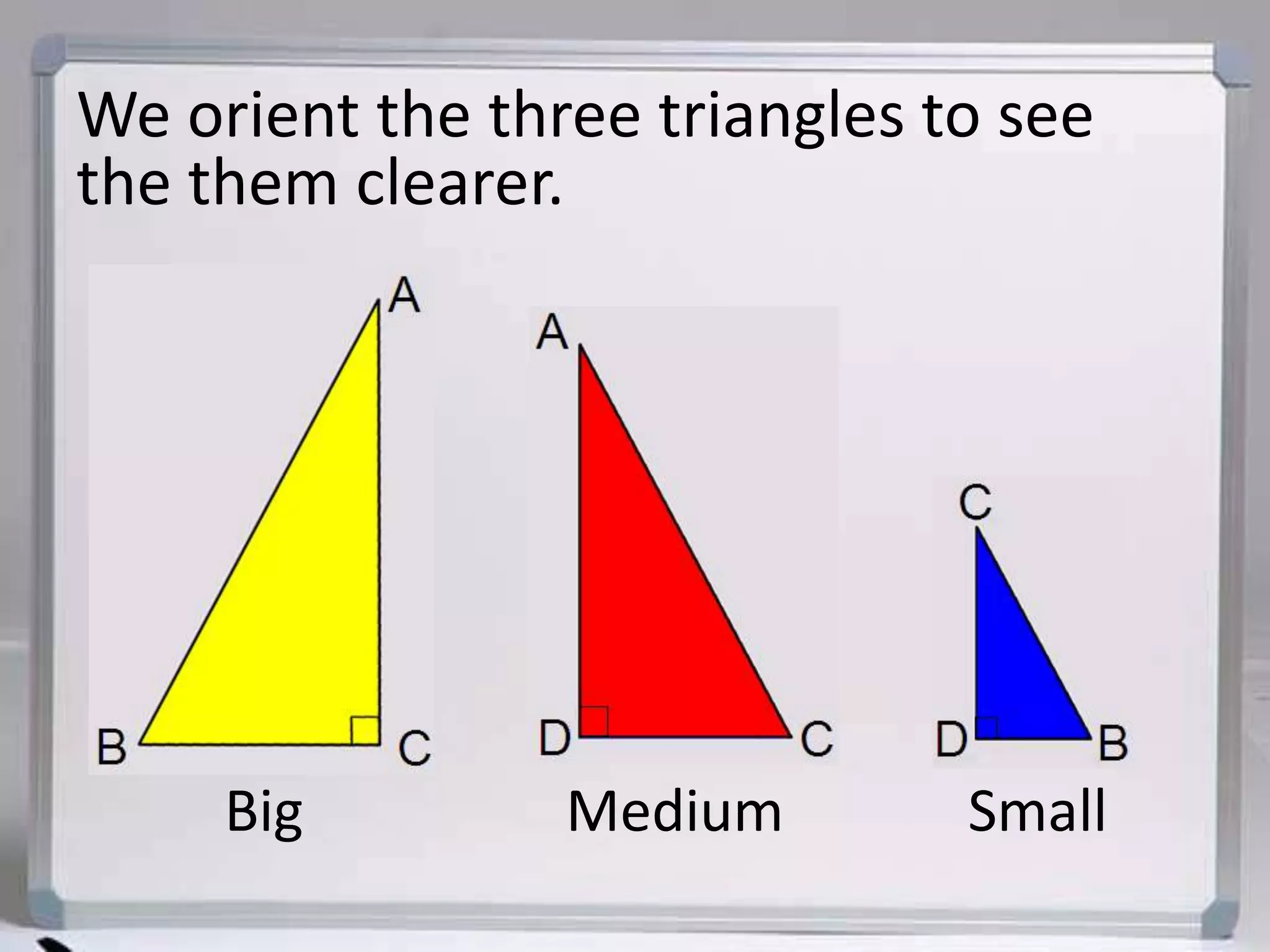
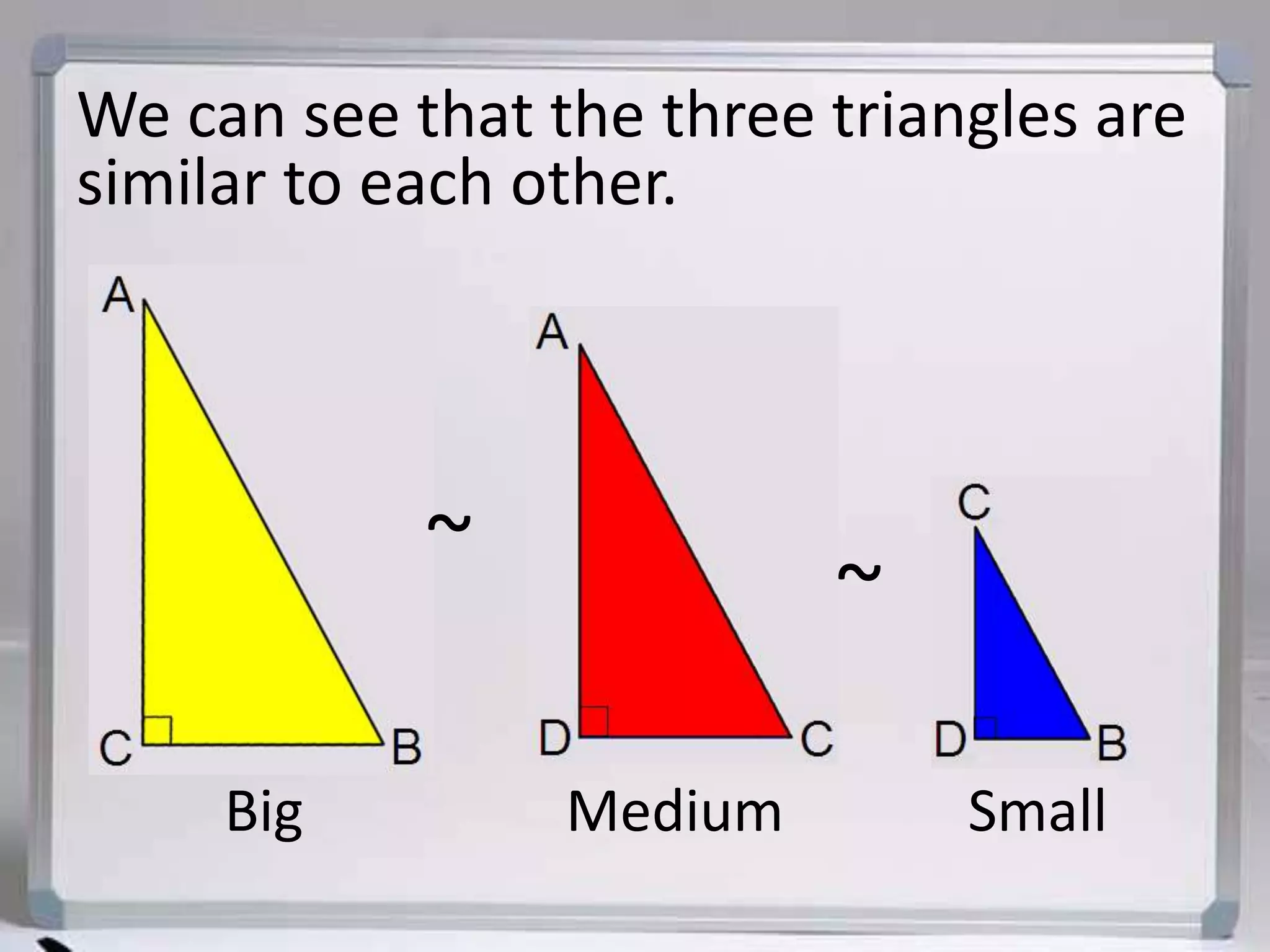
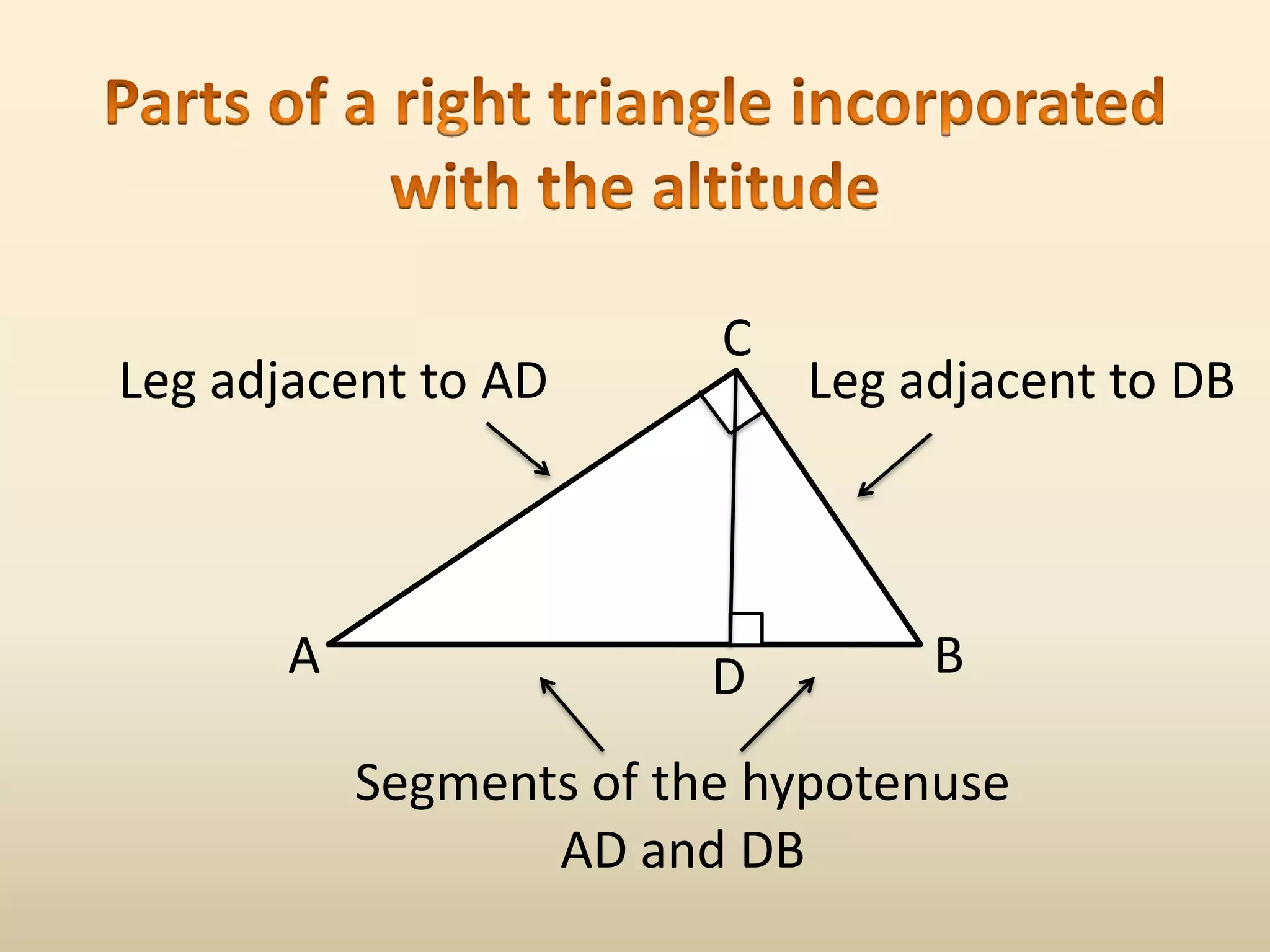
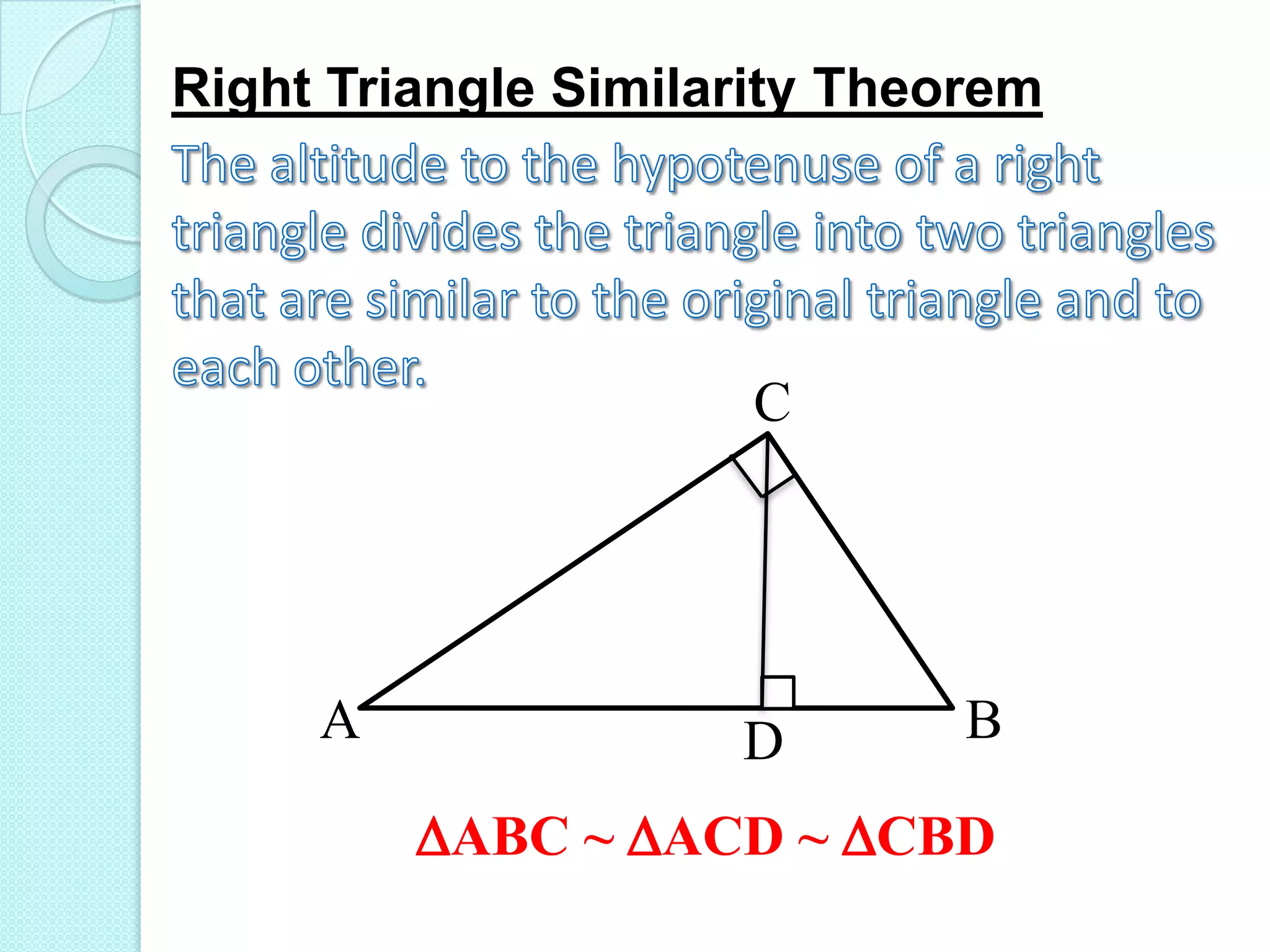
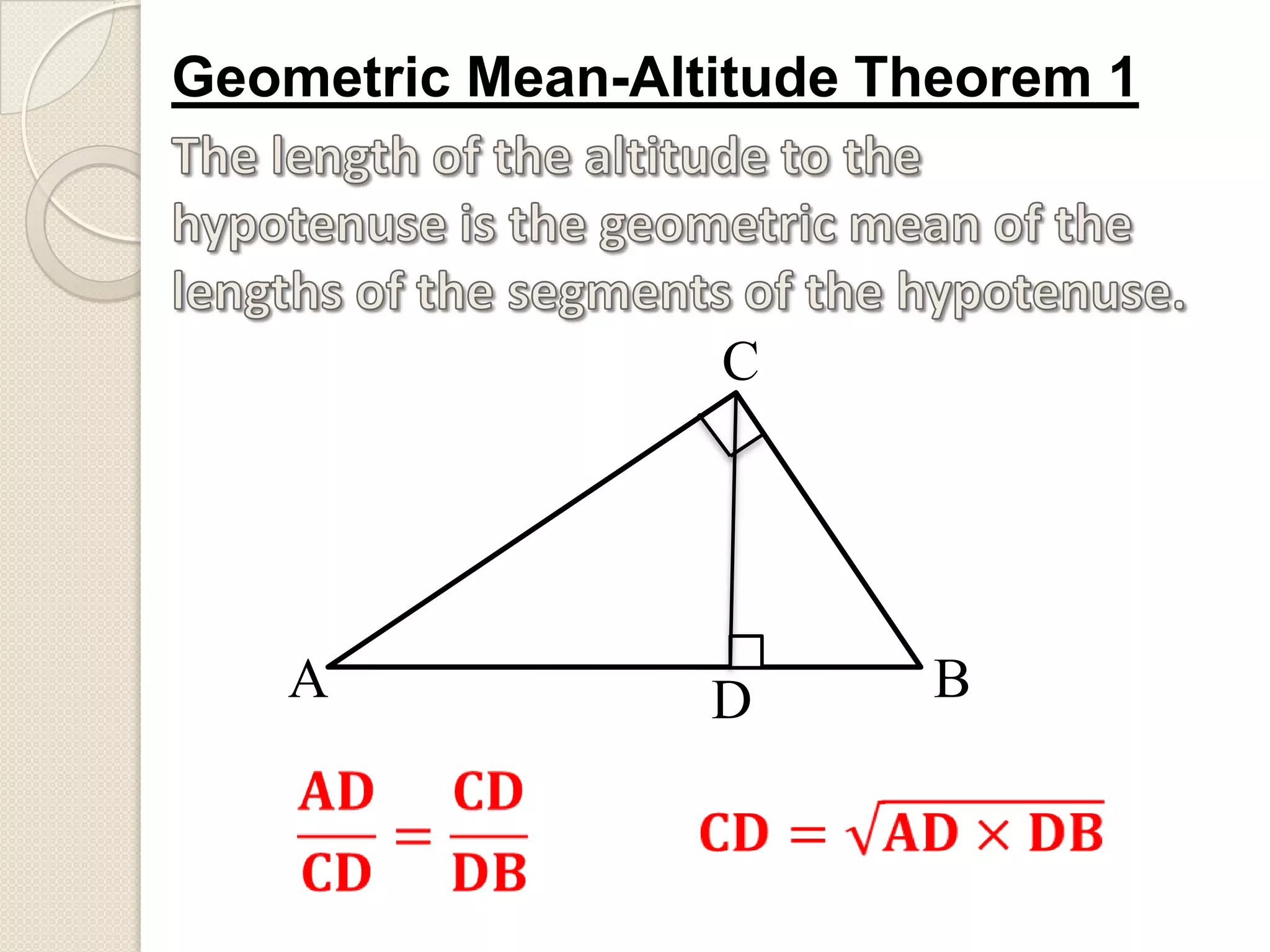
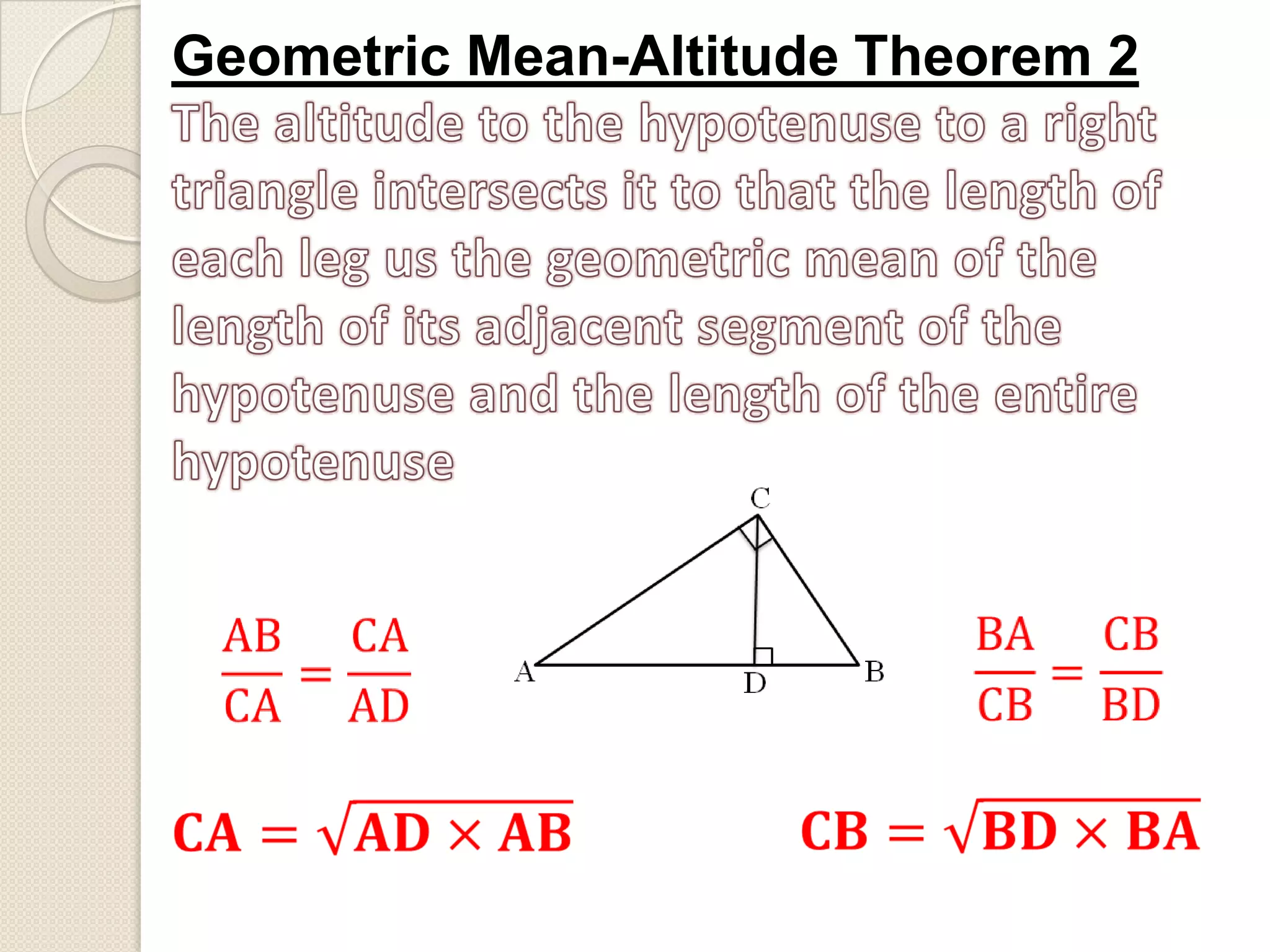
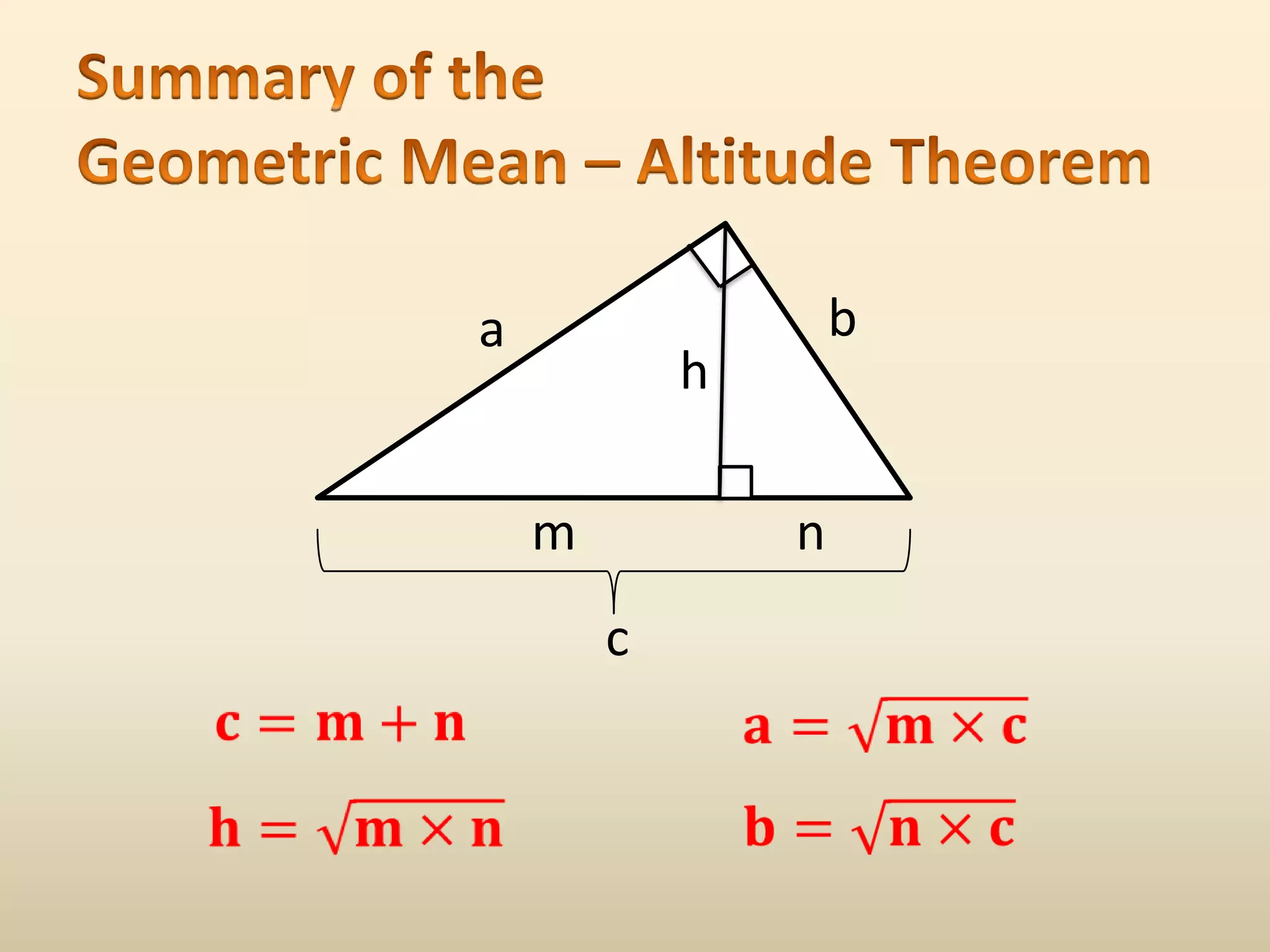
The document discusses similarity in right triangles. It states that drawing an altitude to the hypotenuse of a right triangle divides it into two smaller right triangles that are similar to each other and the original triangle. The altitude also allows one to find missing side lengths using geometric mean formulas. Several examples are given of using these formulas to solve for missing lengths in right triangles.

1. SIMILARITY IN RIGHT TRIANGLES

2. We start with ΔABC.

3. We draw altitude CD to the hypotenuse.

4. This divides the original triangle into two smaller right triangle:

5. This divides the original triangle into two smaller right triangle: ΔDCA

6. This divides the original triangle into two smaller right triangle: ΔBDC

7. There are a three triangles in the figure below.

8. BigMediumSmall

9. BigMediumSmall

10. We orient the three triangles to see the them clearer.BigSmallMedium

11. We can see that the three triangles are similar to each other. ~~BigSmallMedium

12. SIMILARITY IN RIGHT TRIANGLES

13. Parts of a right triangle incorporated with the altitudeCLeg adjacent to DBLeg adjacent to ADABDSegments of the hypotenuse AD and DB

14. Right Triangle Similarity TheoremThe altitude to the hypotenuse of a right triangle divides the triangle into two triangles that are similar to the original triangle and to each other.CABDABC ~ ACD ~ CBD

15. Geometric Mean-Altitude Theorem 1The length of the altitude to the hypotenuse is the geometric mean of the lengths of the segments of the hypotenuse.CABD𝐀𝐃𝐂𝐃=𝐂𝐃𝐃𝐁 𝐂𝐃=𝐀𝐃×𝐃𝐁

16. Geometric Mean-Altitude Theorem 2The altitude to the hypotenuse to a right triangle intersects it to that the length of each leg us the geometric mean of the length of its adjacent segment of the hypotenuse and the length of the entire hypotenuseBACB=CBBD ABCA=CAAD 𝐂𝐁=𝐁𝐃×𝐁𝐀 𝐂𝐀=𝐀𝐃×𝐀𝐁

17. Summary of theGeometric Mean – Altitude Theorembahmnc𝐜=𝐦+𝐧 𝐚=𝐦×𝐜 𝐡=𝐦×𝐧 𝐛=𝐧×𝐜

18. Solve for the other missing lengths given only two measurements.a = 4, b = 6a = 8, c = 10a = 5, m = 7a = 9, n = 6a = 12, h = 9b = 6, c = 15b = 8, m = 9b = 4, n = 3b = 11, h = 8c = 18, m = 12c = 15, n = 8c = 20, h = 6m = 12, n = 8m = 9, h = 12n = 10, h = 12

19. Solve for the other missing lengths given only two measurements.a = 4, b = 6a = 8, c = 10a = 5, c = 8a = 9, m = 6a = 12, h = 9b = 6, c = 15b = 12, n = 9b = 4, n = 3b = 10, h = 6b = 11, h = 8c = 18, m = 12c = 15, n = 8c = 20, m = 6m = 12, n = 8m = 9, h = 12n = 10, h = 12a = 9, m = 6c = 18, m = 12

20. Relating to the Real WorldRecreationAt the parking lot of a State Park, the 300-m path to the snack bar and the 400-m path to the boat rental shop meet at a right angle. Marla walks straight from the parking lot to the ocean. How far is Marla from the snack bar?WHICH IS STRONGER? TRIANGLE OR QUADRILATERAL?