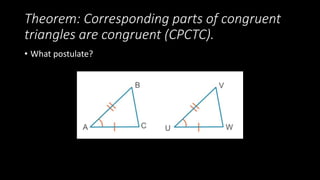
This document discusses congruent triangles and the corresponding parts theorem. It defines the three postulates used to prove congruence: SSS, SAS, and ASA. It provides an example of using the SSS postulate and corresponding parts theorem to show that two angles are congruent and find the exact measure of one of the angles. It emphasizes that corresponding parts theorem can only be used after triangles are shown to be congruent.

1. Math 8 – Congruent
Triangles
Ms. Andi Fullido
© Quipper

2. Objectives
•At the end of this lesson, you
should be able to identify
corresponding congruent parts of
congruent triangles.

3. What are the three postulates used in proving
that two angles are congruent?
•SSS
•SAS
•ASA

4. Theorem: Corresponding parts of congruent
triangles are congruent (CPCTC).

5. Theorem: Corresponding parts of congruent
triangles are congruent (CPCTC).
• What postulate?

6. The following triangles are congruent by the
SSS Postulate.
•If m∠B=2x−5 and
m∠Y=3x−65, what
is the exact
measure of ∠B?

7. Since the two triangles are congruent, we
know via CPCTC that:
•Through the SSS postulate….
•∠A≅∠X
•∠B≅∠Y
•∠C≅∠Z

8. We need an equation to solve for the value of x.
From CPCTC, ∠B and ∠Y are congruent or equal in
measure, then we set both expressions equal to
each other.
•m∠B=m∠Y
•2x−5=3x−65
•65−5=3x−2x
•x=60

9. Use CPCTC in proofs only after showing that
two triangles are congruent.

10. If both triangles ABC and PQR are said to be
congruent, then ∠BAC is congruent to which
angle?

11. Objectives
•At the end of this lesson, you should be
able to write two-column proofs
involving congruent triangles.

12. Given: sBO≅sMA, sOW≅sAN, ∠O≅∠A
Prove: △BOW≅△MAN

13. Proof