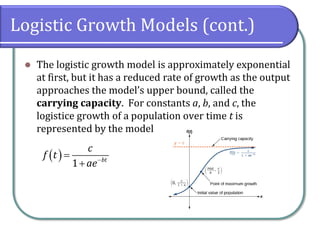
Chapter 6 covers exponential and logarithmic functions, focusing on modeling exponential growth and decay, Newton’s law of cooling, and logistic growth models. It provides formulas for representing these phenomena mathematically, with examples illustrating population dynamics and applications such as carbon-14 dating. Key concepts include the general equations for exponential growth and decay, half-life, and the transition to base e logarithms.