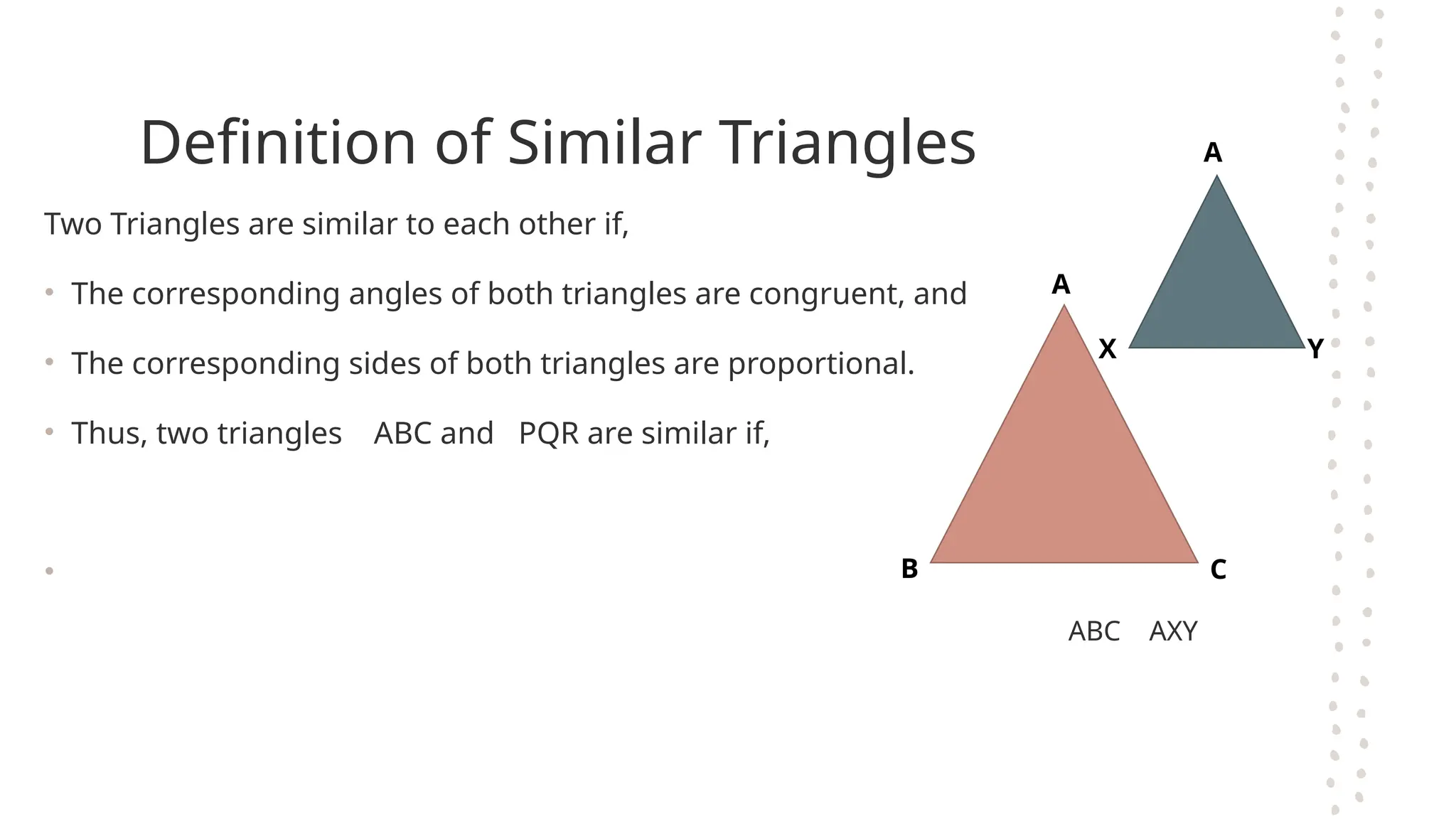
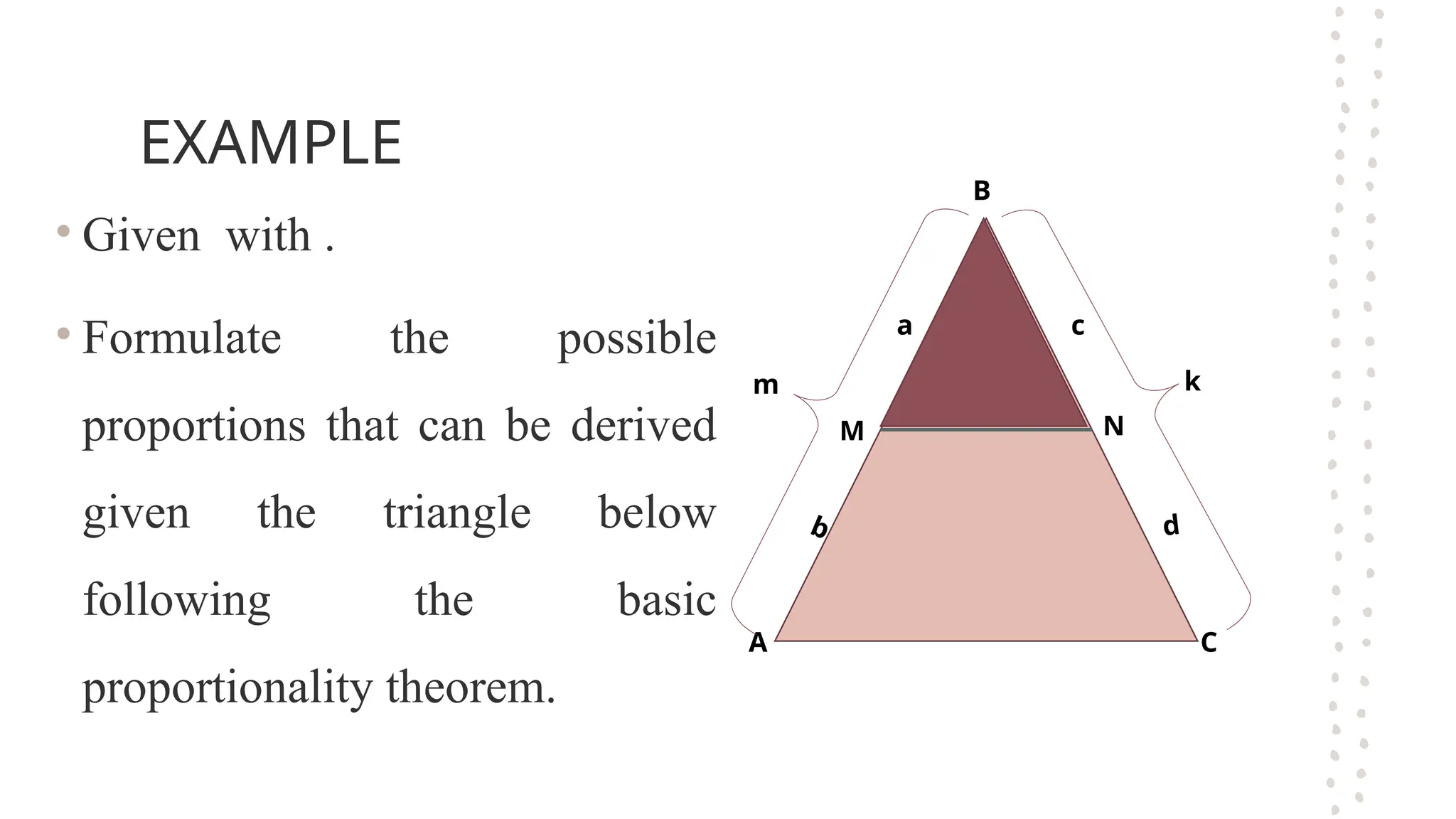
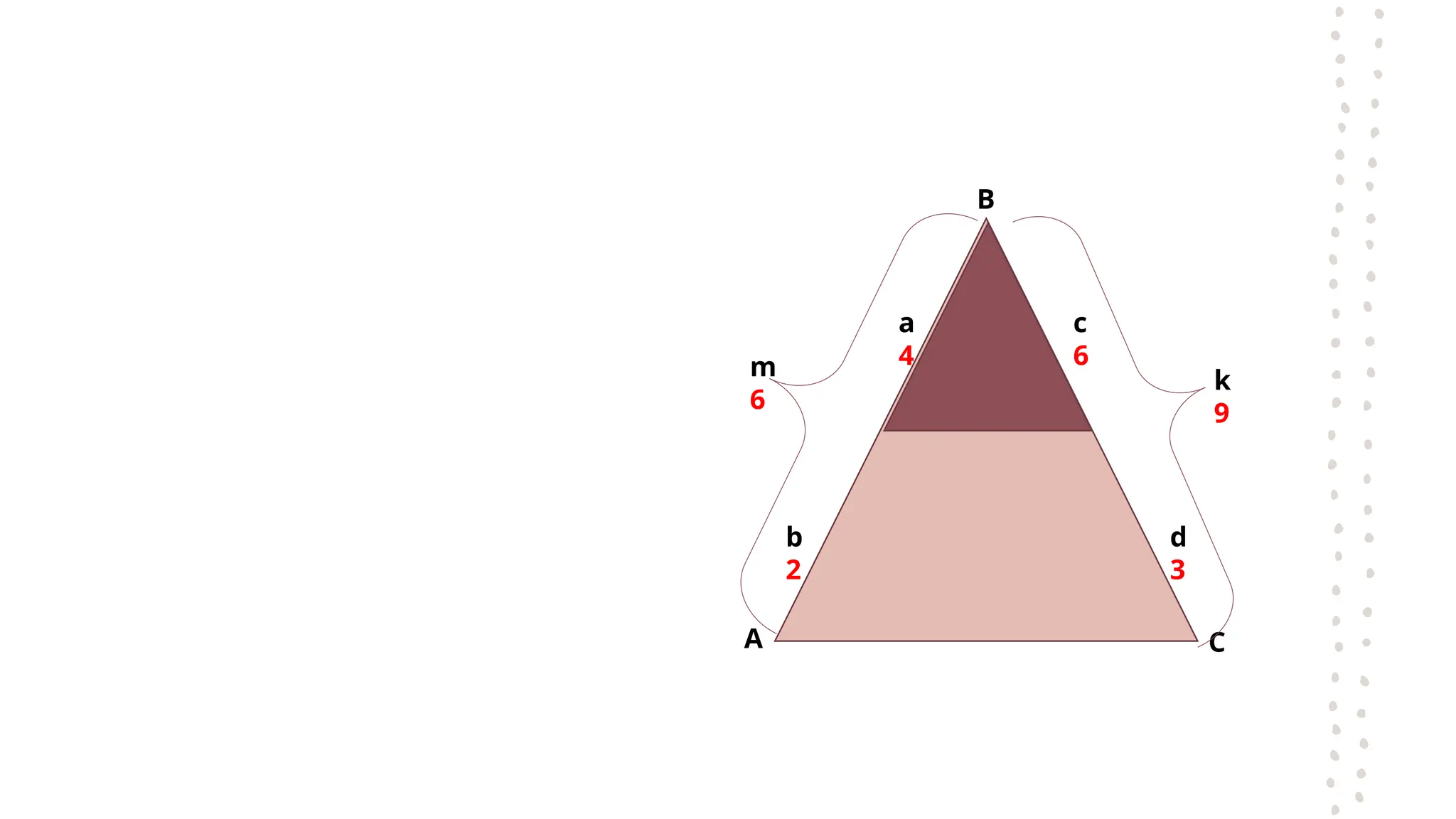
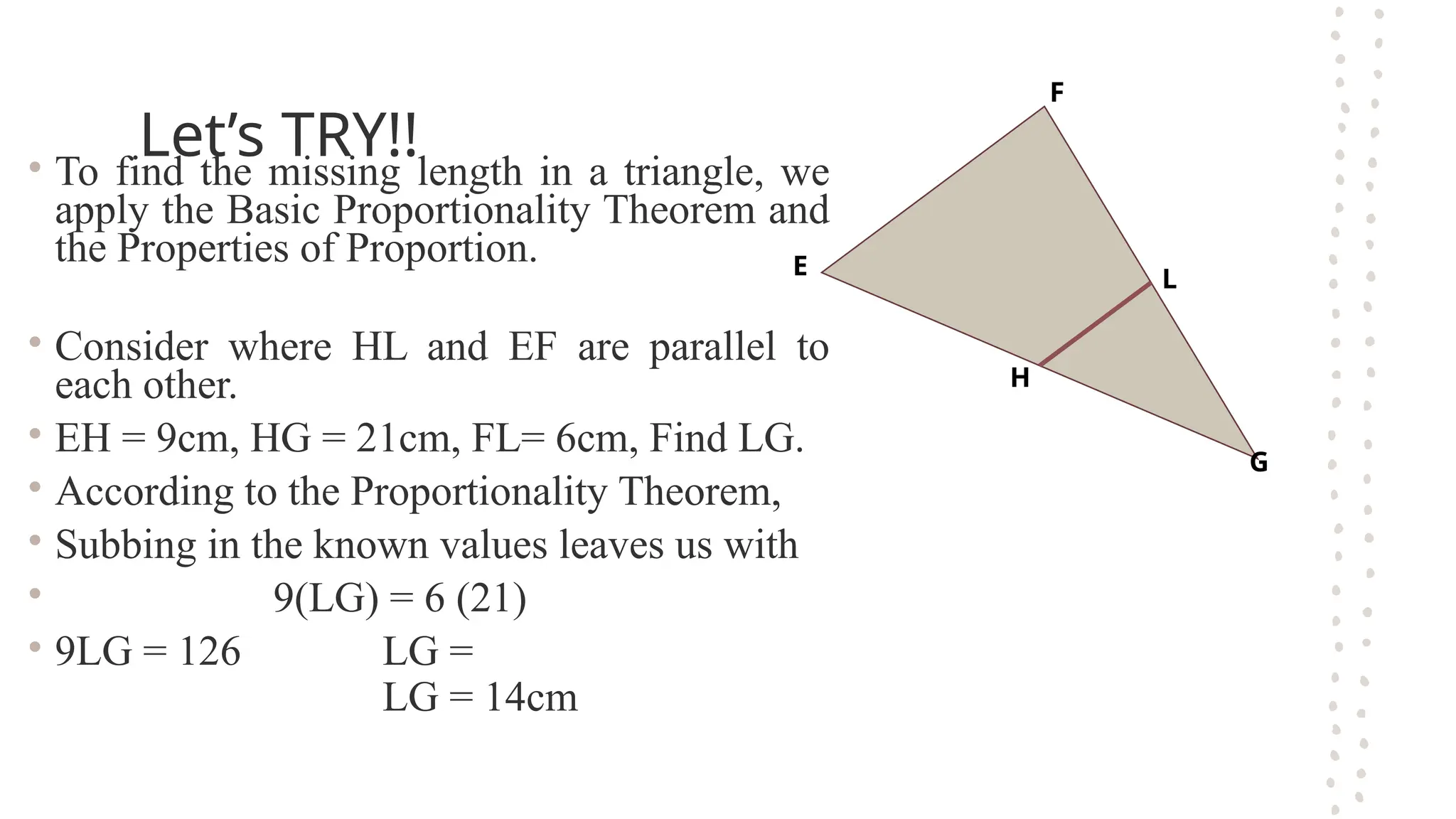
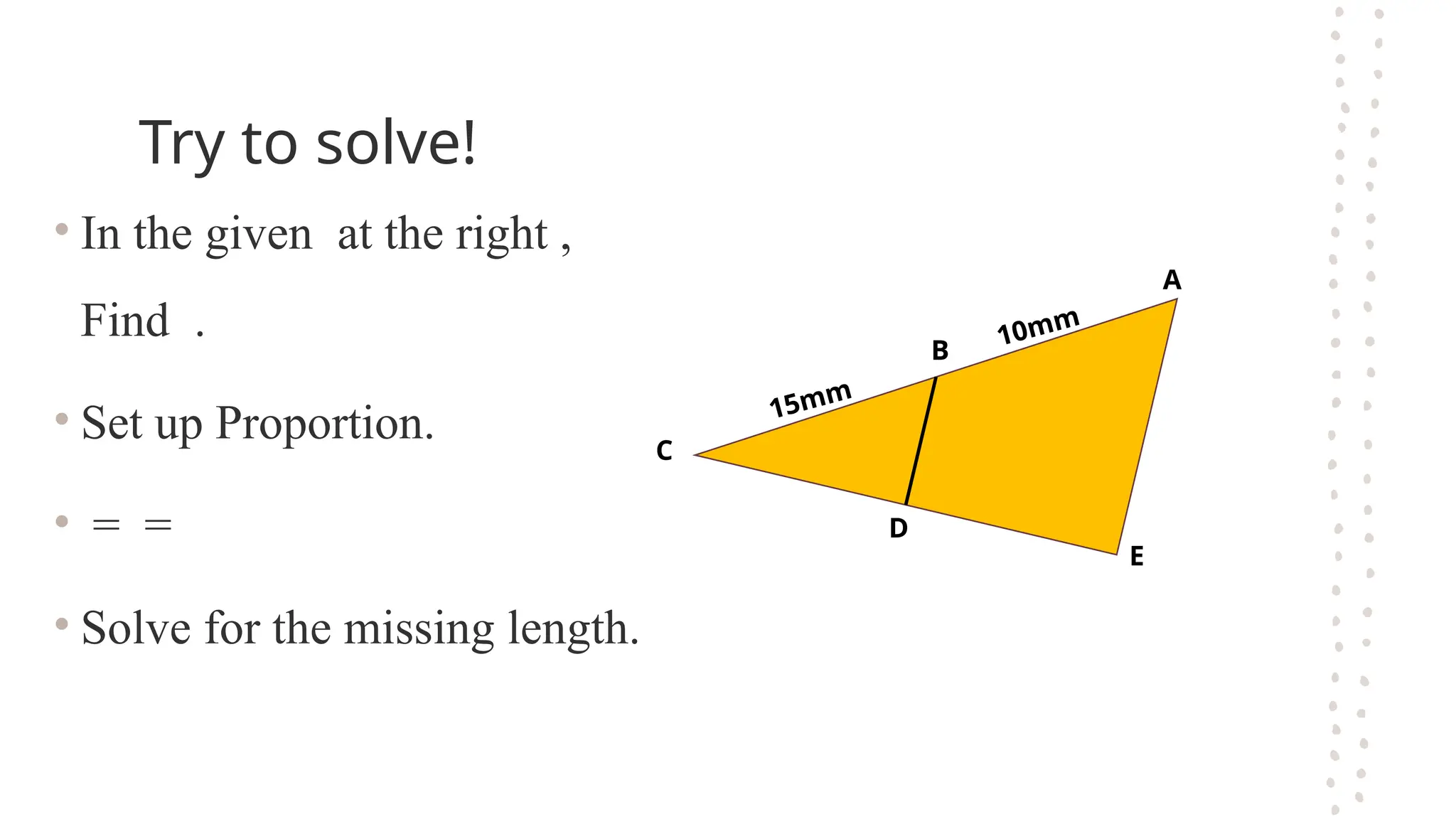
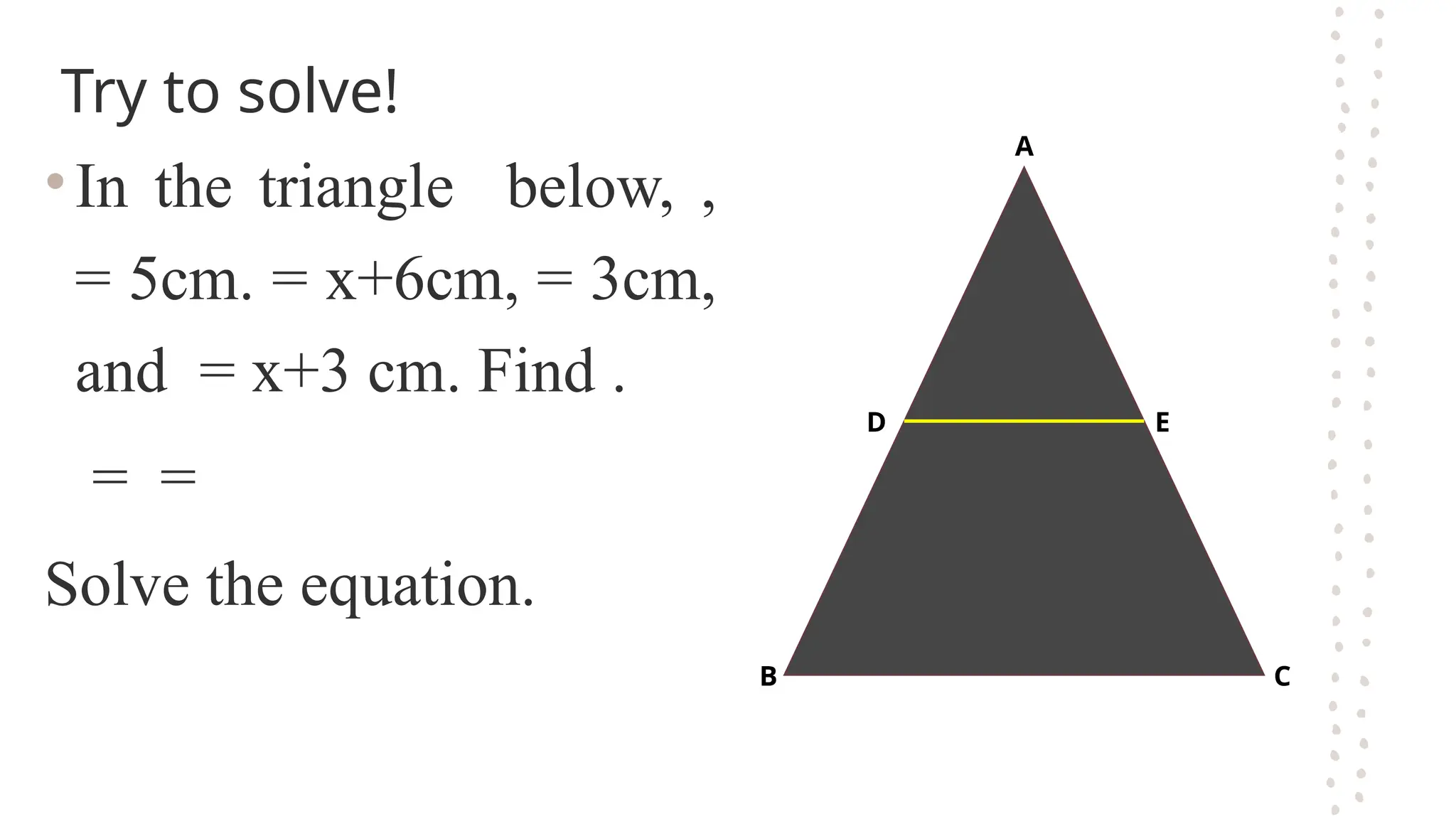
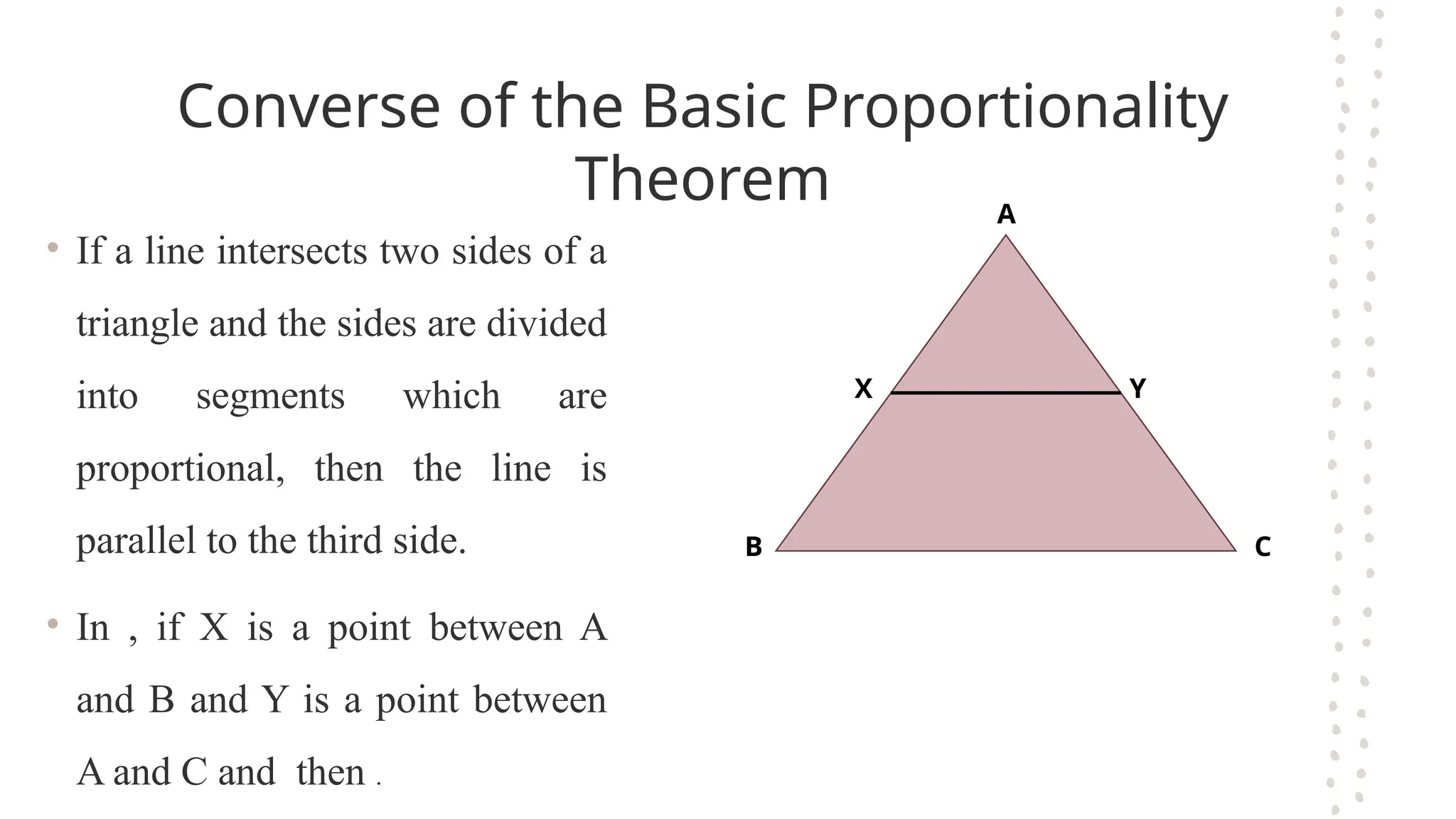
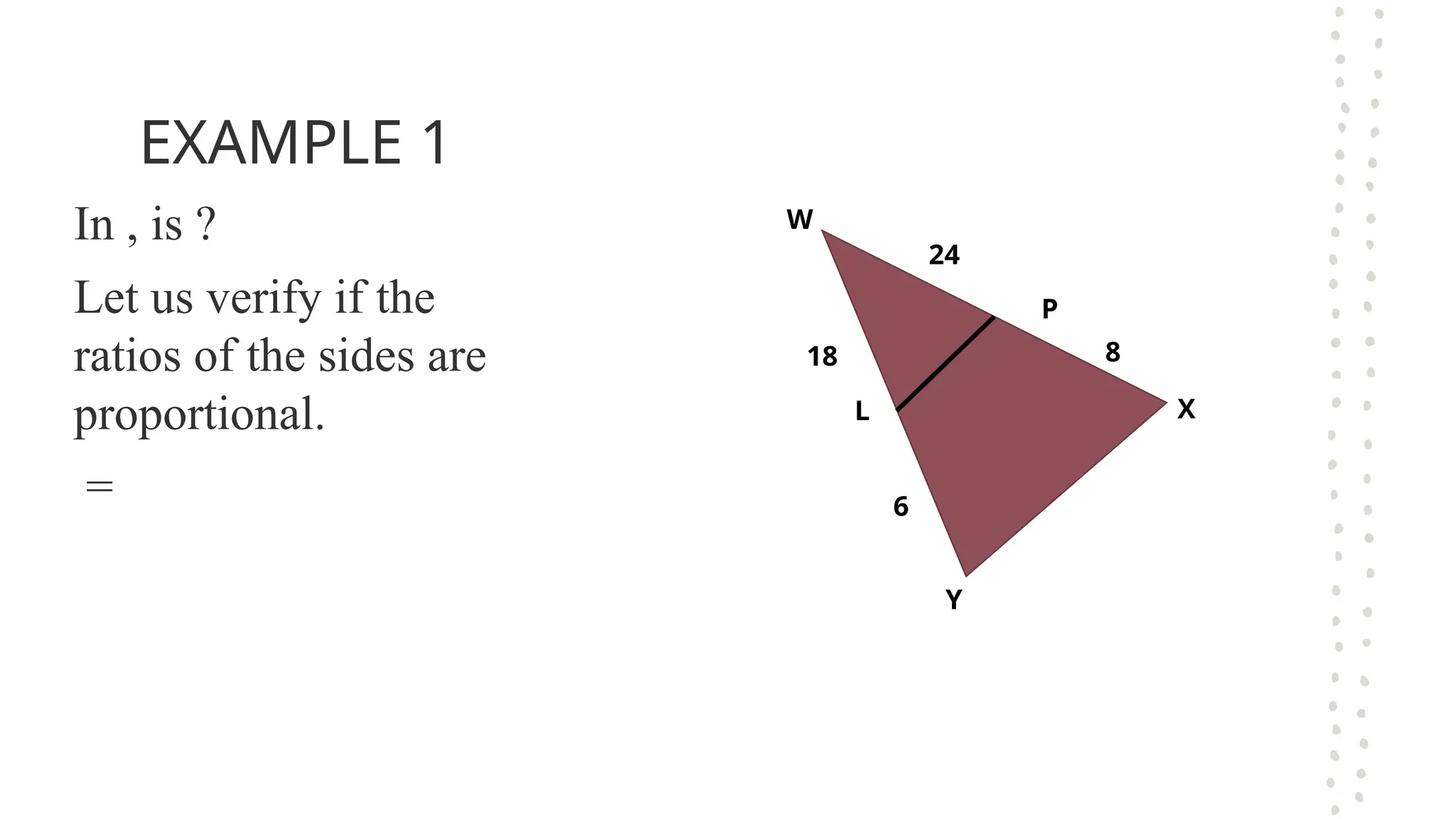
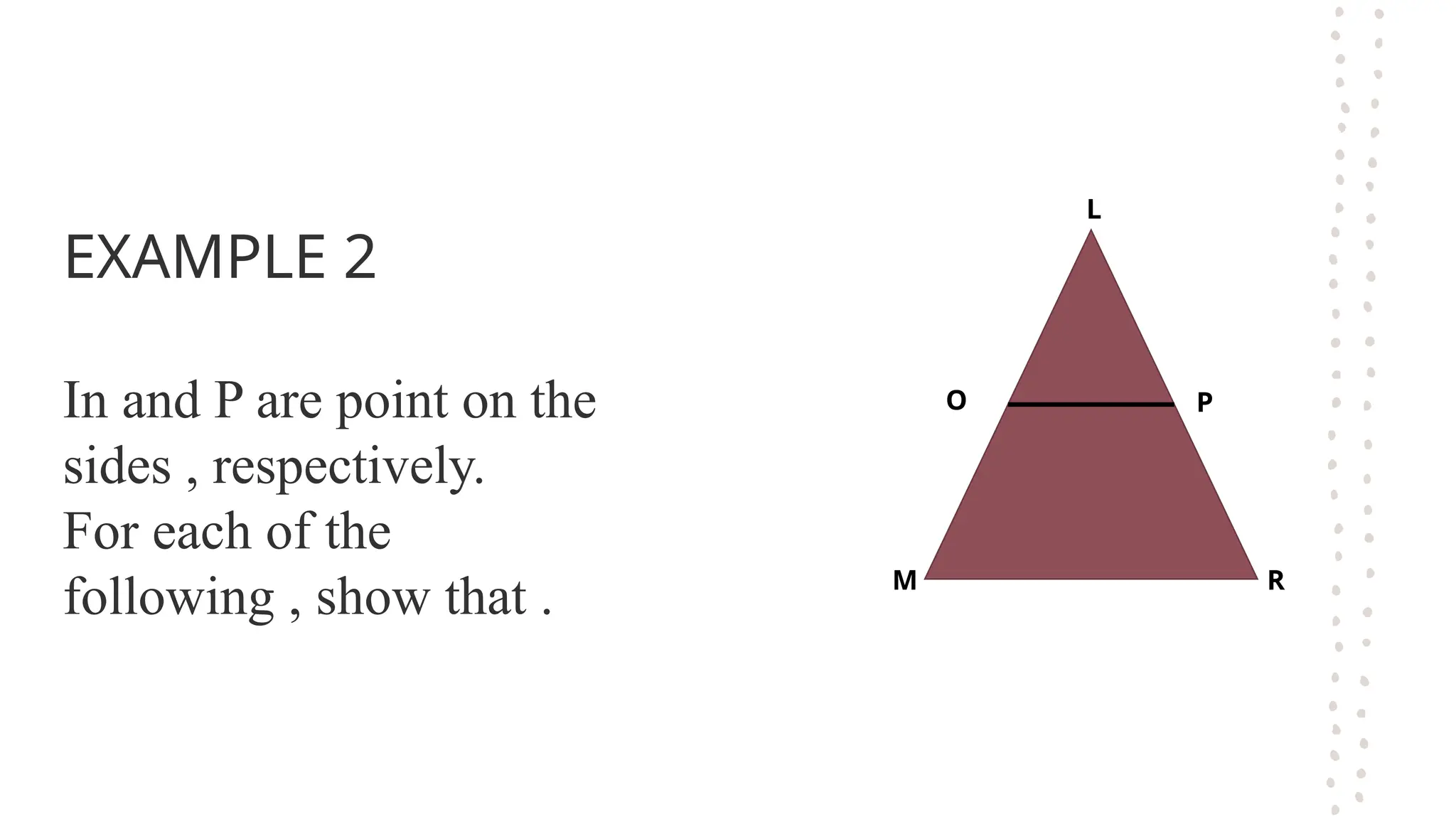
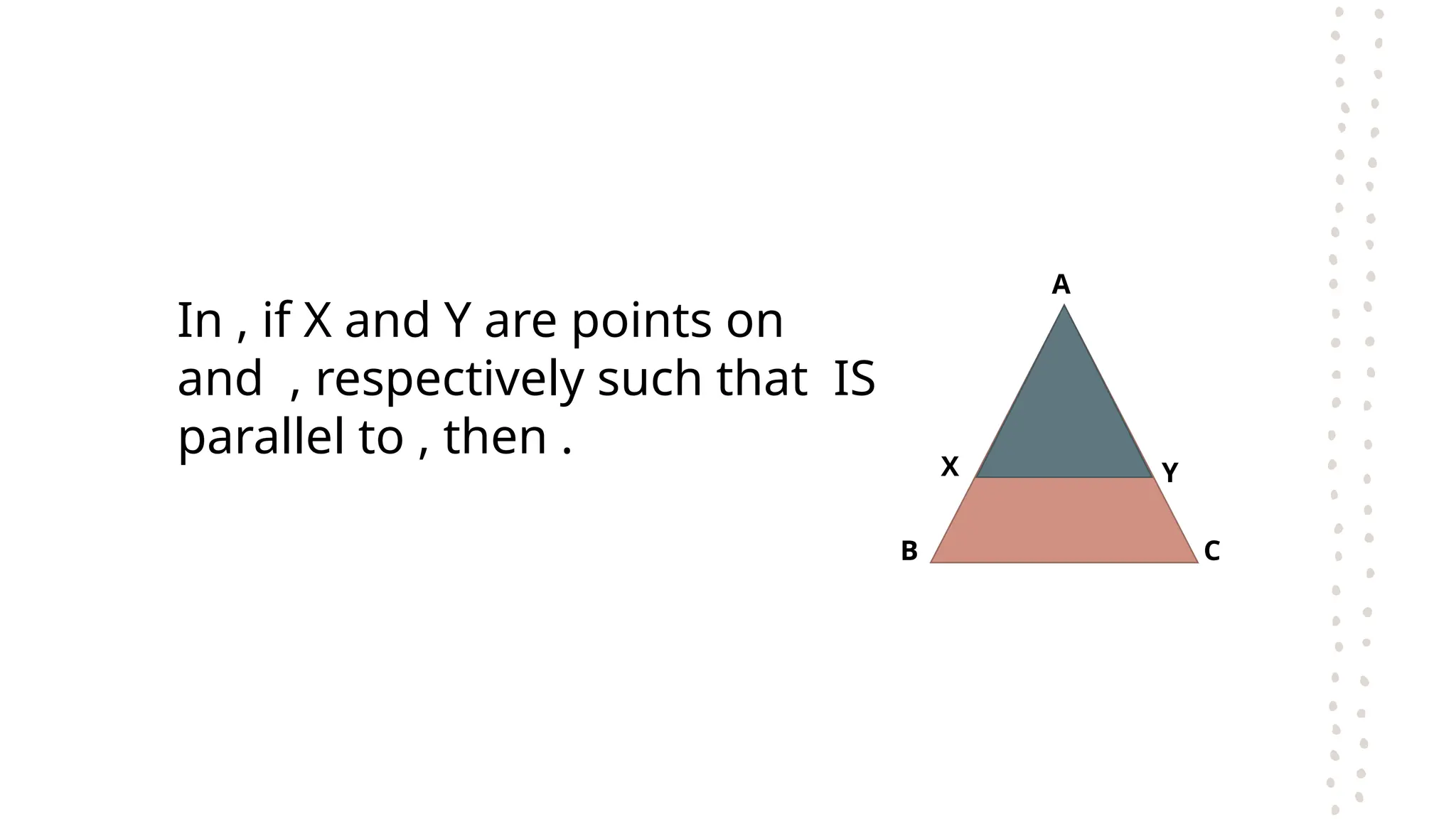The document discusses the fundamental theorems of proportionality, particularly in relation to similar triangles and the basic proportionality theorem (BPT). It explains how to apply these theorems to solve for unknown lengths in triangles by establishing proportions based on corresponding sides and angles. Additionally, it covers the converse of BPT, stating that if a line divides two sides of a triangle proportionally, it is parallel to the third side.

1. Apply the Fundamental
Theorems of
Proportionality to Solve
Problems Involving
Proportion

2. Objective:
1. Applies the Fundamental
Theorems of Proportionality to solve
problems involving Proportions.

3. Definition of Similar Triangles
Two Triangles are similar to each other if,
• The corresponding angles of both triangles are congruent, and
• The corresponding sides of both triangles are proportional.
• Thus, two triangles ABC and PQR are similar if,
•
ABC AXY
B C
A
A
X Y

4. A
B C
X Y
In , if X and Y are points on
and , respectively such that IS
parallel to , then .

5. Basic Proportional Theorem or BPT
• If a line is drawn parallel to one side of a triangle
and intersects the other two sides in distinct points,
then it divides the sides into segments which are
proportional to these sides.
•
A
B C
X Y

6. EXAMPLE
• Given with .
• Formulate the possible
proportions that can be derived
given the triangle below
following the basic
proportionality theorem.
A
B
C
M N
a
b
c
d
k
m

7. A
B
C
a
4
b
2
c
6
d
3
m
6
k
9

8. Let’s TRY!!
• To find the missing length in a triangle, we
apply the Basic Proportionality Theorem and
the Properties of Proportion.
• Consider where HL and EF are parallel to
each other.
• EH = 9cm, HG = 21cm, FL= 6cm, Find LG.
• According to the Proportionality Theorem,
• Subbing in the known values leaves us with
• 9(LG) = 6 (21)
• 9LG = 126 LG =
LG = 14cm
E
F
H
L
G

9. Try to solve!
• In the given at the right ,
Find .
• Set up Proportion.
• = =
• Solve for the missing length.
C
D
E
B
A
15mm
10mm

10. Try to solve!
•In the triangle below, ,
= 5cm. = x+6cm, = 3cm,
and = x+3 cm. Find .
= =
Solve the equation.
B
D
C
E
A

11. Converse of the Basic Proportionality
Theorem
• If a line intersects two sides of a
triangle and the sides are divided
into segments which are
proportional, then the line is
parallel to the third side.
• In , if X is a point between A
and B and Y is a point between
A and C and then .
A
B C
X Y

12. EXAMPLE 1
In , is ?
Let us verify if the
ratios of the sides are
proportional.
=
W
18
L
6
Y
X
8
P
24

13. EXAMPLE 2
In and P are point on the
sides , respectively.
For each of the
following , show that .
L
M R
O P