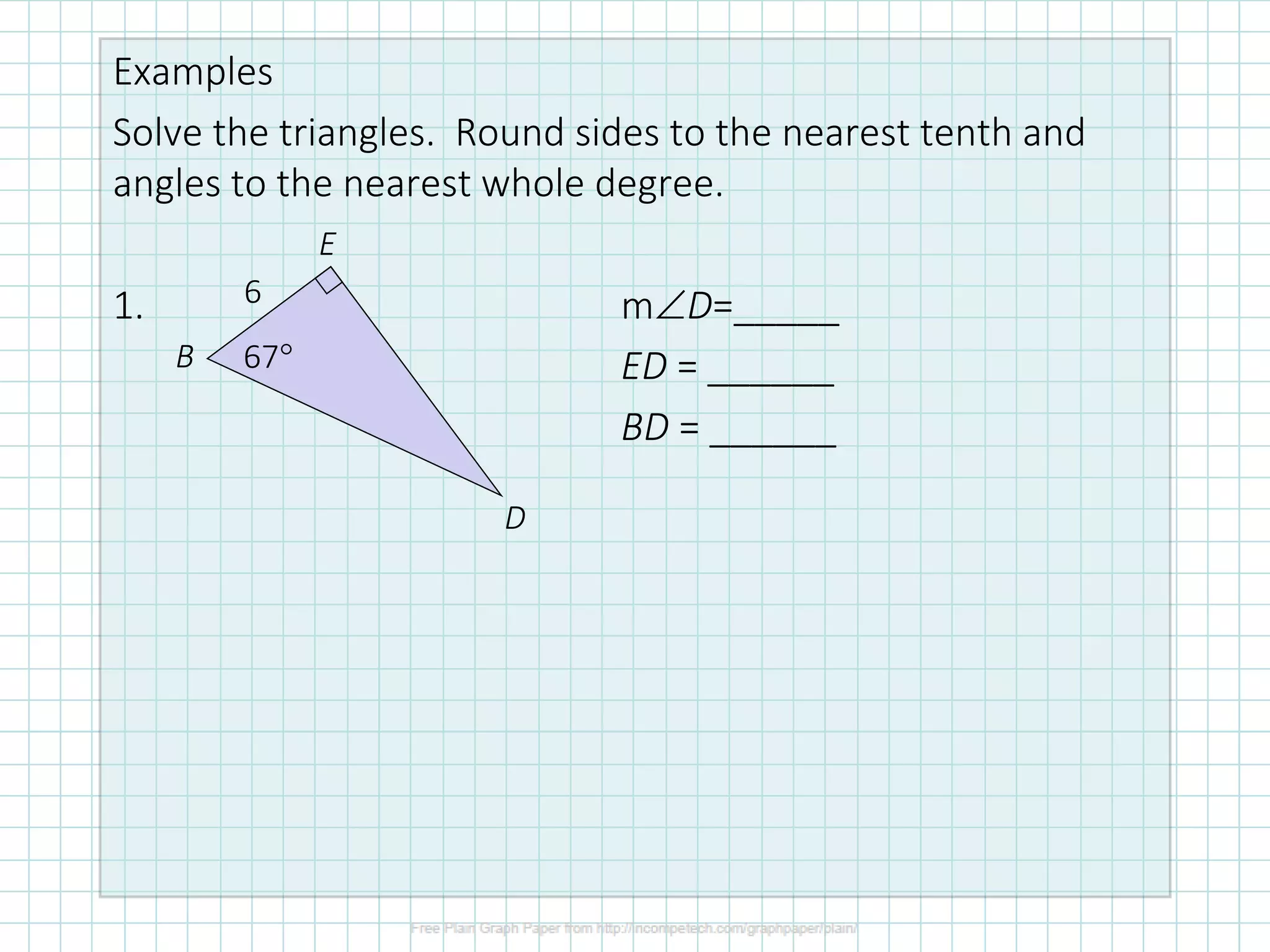
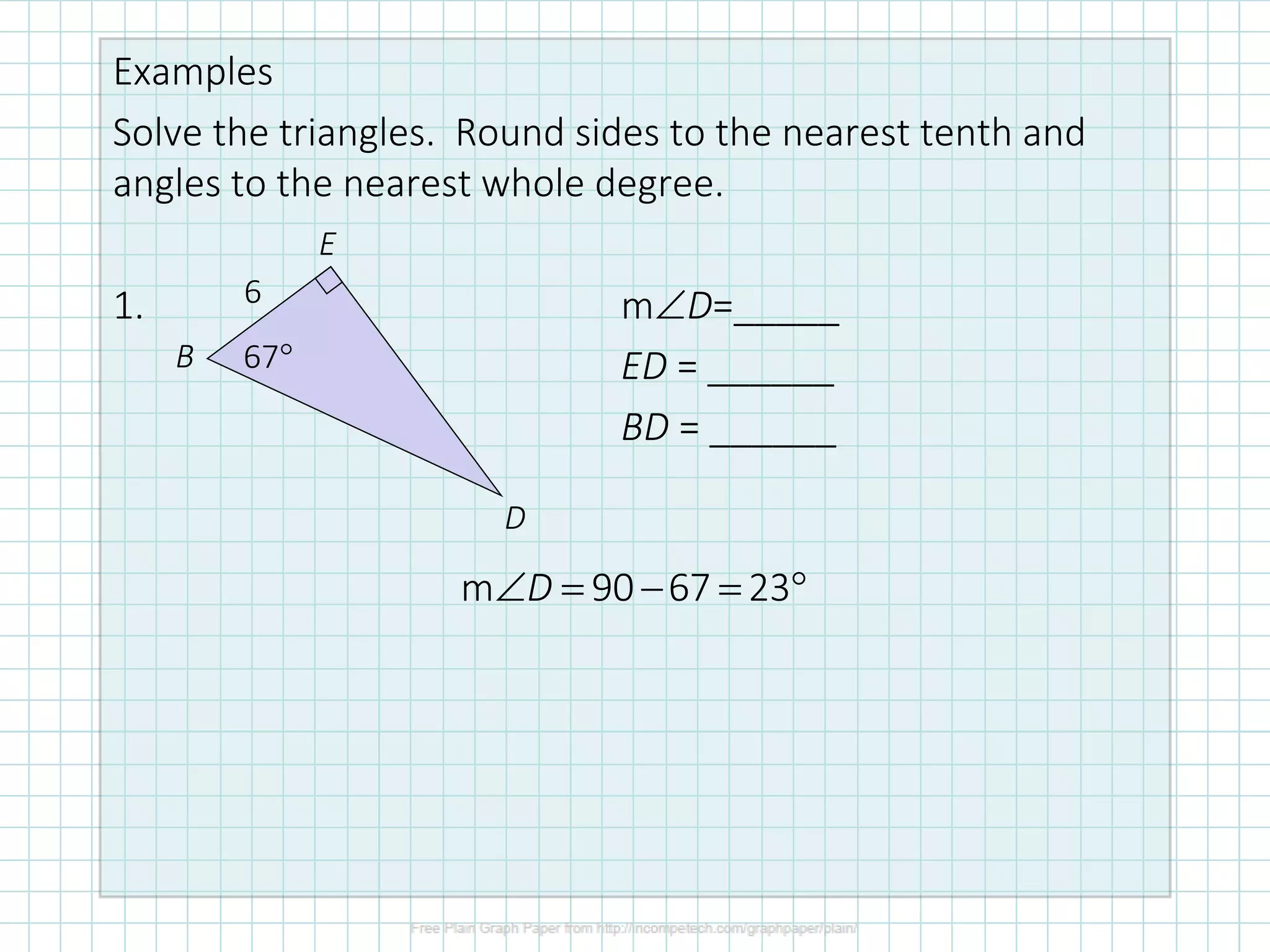
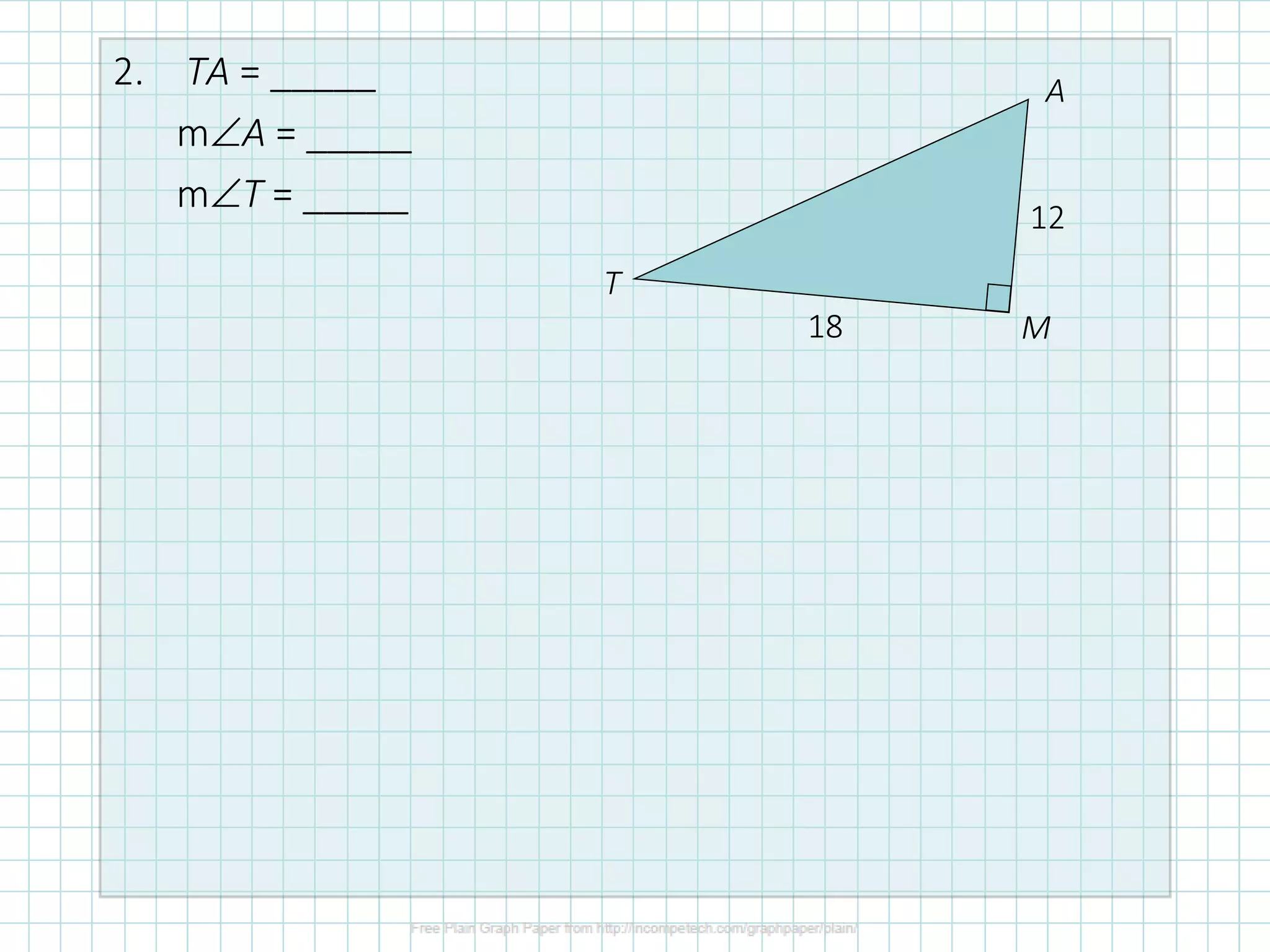
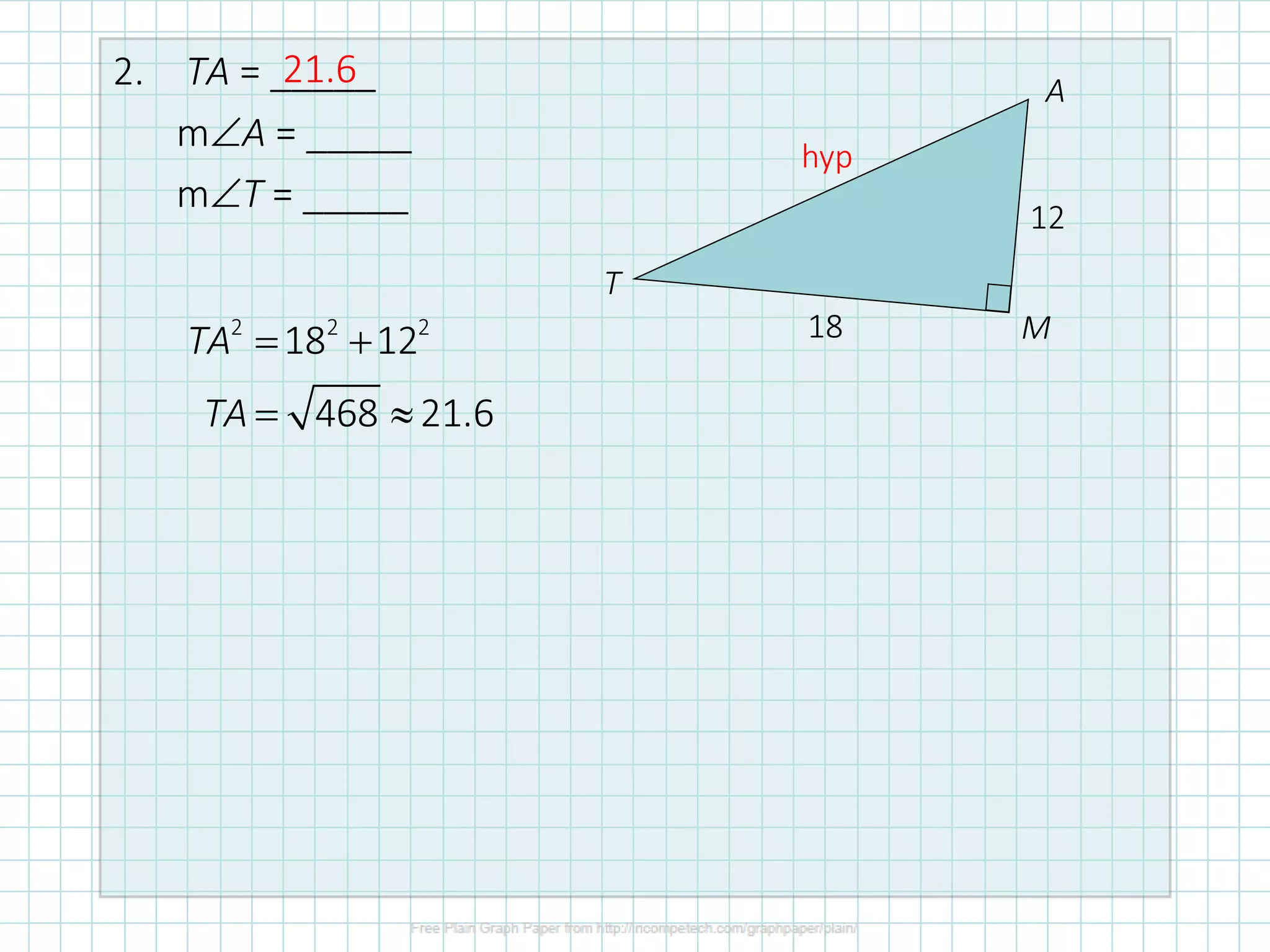
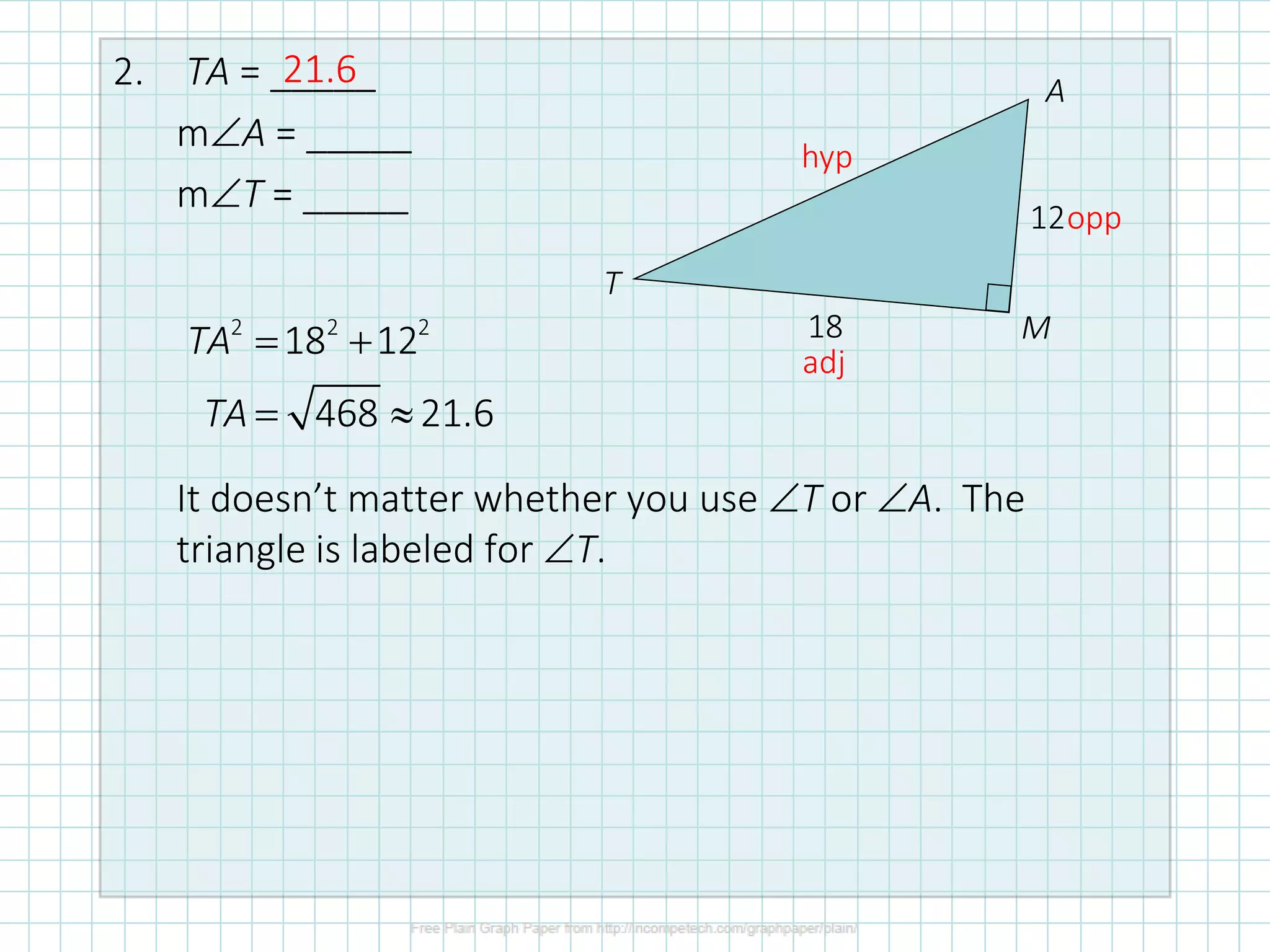
This document discusses how to solve right triangles by finding missing parts. It explains that if an angle and side are given, trigonometric ratios or the Pythagorean theorem can be used to find the other parts. If two sides are given, the Pythagorean theorem or trig ratios can determine the remaining side and angle. Examples demonstrate using trigonometric functions like tangent to calculate missing side lengths or angles in right triangles.

1. Solving Right Triangles
The student is able to (I can):
• Find the missing parts of a right triangle
• Use trig ratios to solve problems

2. To “solve” a right triangle means to find all of the missing
parts of the right triangle.
If you are given an angle and a side:
• Subtract the angle from 90 to find the other acute angle
• Use trig ratios to find one of the missing sides
• Use either trig ratios or Pythagorean Theorem to find the
third side

3. If you are given two sides:
• Use Pythagorean Theorem to find the missing side
• Use trig ratios to find an angle
– Unless all of your sides work out to be whole numbers,
be sure to use the two given sides in your trig ratio to
prevent rounding errors.
• Subtract the angle you found from 90 to find the other
angle

4. Examples
Solve the triangles. Round sides to the nearest tenth and
angles to the nearest whole degree.
1. mD=_____
ED = ______
BD = ______
6
67
B
E
D

5. Examples
Solve the triangles. Round sides to the nearest tenth and
angles to the nearest whole degree.
1. mD=_____
ED = ______
BD = ______
6
67
B
E
D
m 90 67 23
D
 = − = 

6. Examples
Solve the triangles. Round sides to the nearest tenth and
angles to the nearest whole degree.
1. mD=_____
ED = ______
BD = ______
6
67
B
E
D
tan67
6
6tan67
14.1
ED
ED
 =
= 

m 90 67 23
D
 = − = 
23
adj
opp
hyp

7. Examples
Solve the triangles. Round sides to the nearest tenth and
angles to the nearest whole degree.
1. mD=_____
ED = ______
BD = ______
6
67
B
E
D
adj
opp
hyp
tan67
6
6tan67
14.1
ED
ED
 =
= 

m 90 67 23
D
 = − = 
23
14.1

8. Examples
Solve the triangles. Round sides to the nearest tenth and
angles to the nearest whole degree.
1. mD=_____
ED = ______
BD = ______
6
67
B
E
D
adj
opp
hyp
tan67
6
6tan67
14.1
ED
ED
 =
= 

m 90 67 23
D
 = − = 
2 2 2
6 14.1
234.81
15.3
BD
BD
= +
=

23
14.1
15.3

9. 2. TA = _____
mA = _____
mT = _____
12
18
T
A
M

10. 2. TA = _____
mA = _____
mT = _____
12
18
T
A
M
2 2 2
18 12
468 21.6
TA
TA
= +
= 
hyp
21.6

11. 2. TA = _____
mA = _____
mT = _____
It doesn’t matter whether you use T or A. The
triangle is labeled for T.
12
18
T
A
M
2 2 2
18 12
468 21.6
TA
TA
= +
= 
hyp
opp
adj
21.6

12. 2. TA = _____
mA = _____
mT = _____
It doesn’t matter whether you use T or A. The
triangle is labeled for T.
12
18
T
A
M
2 2 2
18 12
468 21.6
TA
TA
= +
= 
hyp
opp
adj
1
12
tan
18
12
tan
18
34
T
T −
=
 
=  
 
 
90 34
56
m A
 = −
= 
21.6
56
34