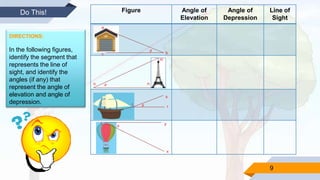
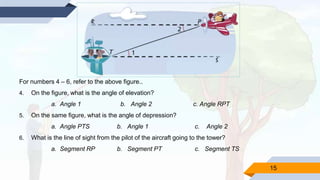
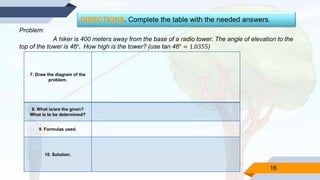
This document provides a strategic intervention material to help students learn about solving real-life problems involving right triangles using trigonometric ratios. It begins with definitions of key terms like line of sight, angle of elevation, and angle of depression. Students are given examples of problems involving these angles and their solutions. Later activities require students to illustrate problem situations, identify given information, formulas used, and solve problems determining unknown angles or distances. The material aims to supplement classroom learning and help students independently practice and understand solving right triangle problems.

1. A Strategic Intervention Material in Mathematics IX
Prepared by:
Brian M. Mary
Sta. Cruz National High School –Lipay High School
School I.D.: 301034
Magsaysay Park, Pob. South, Sta. Cruz, Zambales

2. HELLO!
Iamthe TwentySixth Baam.‘Baam’for short.
I am heretobeyourguide asyoutrytounravel
the mysterythatis called the
AngleofElevation&Angleof Depression.
2
GOODLUCK!
26 𝑡ℎ
GUIDE CARD

3. 3
A few reminders…
PURPOSE OF THIS STRATEGIC INTERVENTION MATERIAL (SIM)
This learning package is intended to supplement your classroom learning while
working independently . The activities and exercises will widen your understanding of the
different concepts (of angles of elevation and angles of depression) you should learn.
HOW TO USE THIS STRATEGIC INTERVENTION MATERIAL (SIM)
• Keep this material neat and clean.
• Thoroughly read every page.
• Follow carefully all instructions indicated in every activity.
• Answer all questions independently and honestly.
• Write all your answers on a sheet of paper.
• Be sure to compare your answers to the KEY TO CORRECTIONS only after you
have answered the given tasks.
• If you have questions or clarifications, ask your teacher.
Havea good time
learning!

4. “Mathematics is not about
numbers, equations,
computations, or algorithms: it is
about understanding.
44

5. TASK ANALYSIS
LEAST MASTERED SKILLS
▰Use of Trigonometric Ratios in Solving Real-Life Problems
Involving Right Triangles
Sub Tasks
▰Illustrates angles of elevation and angles of depressions
▰Distinguish between angles of elevations and angles of
depressions
▰Solve problems involving right triangles
5

6. 6
OVERVIEW
Trigonometry - the branch of Mathematics that studies
relationship involving the lengths and angles of a triangle. The word
“Trigonometry” is derived from the Greek words, “Tri” (meaning three),
“Gon” (meaning sides), and “Metron” (meaning measure).
There are six functions of an angle used in trigonometry. Their
names and abbreviations are sine (sin), cosine (cos), tangent (tan),
cotangent (cot), secant (sec), and cosect (cos).
Trigonometric functions are used in obtaining unknown angles
and distance from known and measured angles in geometric figures. It
developed from a need to compute angles and distances in such fields
as Astronomy, Map Making, Surveying, etc.Problems involving angles
and distances in one plane are covered din Plane Trigonometry.
In this SIM, trigonometry is used to solve for particular real-life
problems involving right triangles.

7. 7
Suppose you are on top of a mountain and
looking down at a certain village, how will you
directly mesure the height of the mountain? An
airplane is flying at a certain height above the
ground. Is it possible to find the distance along
the ground from the airplane to an airport using
a ruler?
The trigonometric ratios as you have
learned in previous lessons will help you
answer these questions. Perform the
succeeding activities to apply these
concepts in real – life problems.
I hopeyoustillremember
theselessons…
Let’s Start.

8. ACTIVITY 1
Solving real-life problems involving right triangles requires knowledge of some
significant terms such as line of sight, angle of elevation, and angle of depression.
Let’s study the following definitions.
8
Line of Sight – an imaginary line that connects
the eye of an observer to the object being
observed.
The angle of elevation – is the angle from the
horizontal to the line of sight of the observer to
the object above.
The angle of depression – is the angle from
the horizontal to the line of sight of the
oberver to the object below.
Look Up! Look Down!

9. 9
Do This! Figure Angle of
Elevation
Angle of
Depression
Line of
Sight
DIRECTIONS:
In the following figures,
identify the segment that
represents the line of
sight, and identify the
angles (if any) that
represent the angle of
elevation and angle of
depression.
a
bc
m
no 𝜃
𝜃
𝜃
𝜃
r
s
t
y
x
z

10. 10
ACTIVITY 2 Process Me!
The study of trigonometric ratios originated from geometric problems involving
triangles. Solving a trriangle means finding the lengths of the sides and the measures
of the angles of the triangle. Trigonometric ratios may be used to solve problems
involving angles of elevation and depression.
EXAMPLE 1.
A building is 15.24 m high. At a certain
distance from the building, an observer
determines that the angle of elevation
to the top is 41°. How far is the
observer from the base of the tower?
(use tan 41° = 0.8693)
15.24
Observer’s eye
𝜃 = 41°

11. 11
15.24
41°
x
GIVEN:
𝜃= 41° Formula: tan 𝜃 =
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡
opposite = 15.24 SOLUTIONS: tan 41° =
15.24
𝑥
adjacent = x x tan 41° = 15.24
x =
15.24
tan 41°
x =
15.24
0.8693
x = 17.53
Iftwolegsofthetrianglearepartoftheproblem,thenitisa tangentratio.
Ifthehypotenuseispartoftheproblem,thenitiseithera sineorcosine
ratio.

12. 12
EXAMPLE 2.
An airplane is flying at a certain height
above the ground. The distance along the
ground from the airplane to an airport is 6
kilometers. The angle of depression of the
airplane to the airport is 33.69°. Determine
the height of the airplane from the ground.
(use tan 33.69° = 0.6667)
x
6 km
path of plane
θ = 33.69°
GIVEN: Formula: tan 𝜃 =
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡
𝜃 =
33.69°
adjacent = 6 km SOLUTIONS: tan 33.69° =
𝑥
6 𝑘𝑚
opposite = x
x = tan 33.69° (6 km)
x = 0.6667 (6 km)
x = 4 km
Itisveryimportanttoillustratethe
situationsoyoucan visualizeit
properly.

13. Do This! DIRECTIONS: Illustrates the situations presented by the information then solve
the problem.
PROBLEM 1.
The angle of elevation of the top of a
building from a point 30 meters away from
the building is 65°. Find the height of the
building. (use tan 65° =2.1445)
PROBLEM 2.
A bird sits on top of a 5 – meter lamppost.
The angle of depression from the bird to
the feet of an observer is 35°. Determine
the distance of the observer from the
lamppost. (use tan 35° = 0.7002)
Draw the diagram
of the problem.
What is/are the
given?
What is to be
determined?
Formulas used.
Solution.
Draw the diagram
of the problem.
What is/are the
given?
What is to be
determined?
Formulas used.
Solution.

14. 14
ASSESSMENT CARD
DIRECTIONS. Choose the letter that best answer the questions.
1. This angle is from the horizontal to the line of sight of the observer to the object above.
a. Line of Sight b. Angle of Depression c. Angle of Elevation
2. Is an imaginary line that connects the eye of the observer to the object being observed.
a. Angle of Elevation b. Line of Sight c. Angle of Depression
3. This angle is from the horizontal to the line of sight of the observer to the object below.
a. Angle of Depression b. Line of Sight c. Angle of Elevation
Itisnowtimetouse thoseskillsyou
havelearnedsofar.I believein you!
Goodluck!

15. 15
For numbers 4 – 6, refer to the above figure..
4. On the figure, what is the angle of elevation?
a. Angle 1 b. Angle 2 c. Angle RPT
5. On the same figure, what is the angle of depression?
a. Angle PTS b. Angle 1 c. Angle 2
6. What is the line of sight from the pilot of the aircraft going to the tower?
a. Segment RP b. Segment PT c. Segment TS

16. 16
Problem:
A hiker is 400 meters away from the base of a radio tower. The angle of elevation to the
top of the tower is 46°. How high is the tower? (use tan 46° = 1.0355)
7. Draw the diagram of the
problem.
8. What is/are the given?
What is to be determined?
9. Formulas used.
10. Solution.
DIRECTIONS. Complete the table with the needed answers.

17. ENRICHMENT CARD
A clinometer is a tool that is used to measure the angle
of elevation, or angle from the ground, in a right - angled
triangle. You can use a clinometer to measure the height of
tall things that you can't possibly reach, like the top of flag
poles, buildings, trees.
For more on how to make an improvised clinometer, visit the
following web page: http://www.instructables.com/id/Basic-
Clinometer-From-Classroom-Materials/
17
Did you know you can measure tall
objects with ease with the use of
trigonometry and a certain device?
This device is a celled a CLINOMETER.

18. ▰Learner’s Material for Mathematics 9, pp. 427 – 473.
▰Teaching Guide for Mathematics 9 LM
▰SlideCarnival & Startup Start Photos
▰http://www.instructables.com/id/Basic-Clinometer-From-
Classroom-Materials/
18
REFERENCES CARD

19. 19
KEY TO CORRECTIONS
ACTIVITY 1. ACTIVITY 2. PROBLEM 1.
Draw the
diagram of the
problem.
What is/are the
given?
What is to be
determined?
𝜃 = 65°
Adjacent = 30
Opposite = x
Formulas used. tan 𝜃 =
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡
Solution.
tan 65° =
𝑥
30
𝑥 = tan 65° (30)
𝑥 = 64.34 𝑚𝑒𝑡𝑒𝑟𝑠
x
65°30
Good work!Iknowyouhaveitin you!
Justkeepstudyingdude!

20. 20
ASSESSMENT CARD.
ACTIVITY 2. PROBLEM 2.
Draw the
diagram of the
problem.
What is/are the
given?
What is to be
determined?
𝜃 = 35°
Opposite = 5
Adjacent = x
Formulas used. tan 𝜃 =
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡
Solution.
tan 35° =
5
𝑥
𝑥 =
5
tan 35°
𝑥 = 7.14 𝑚𝑒𝑡𝑒𝑟𝑠
1. C 2. B 3. A 4. A 5. C 6. B
7. Draw the
diagram of the
problem.
8. What is/are
the given?
What is to be
determined?
𝜃 = 46°
Adjacent = 400
Opposite = x
9. Formulas
used.
tan 𝜃 =
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡
10. Solution.
tan 46° =
𝑥
400
𝑥 = tan 46° (400)
𝑥 = 414.21 𝑚𝑒𝑡𝑒𝑟𝑠
x
x
55
35°
46°400
x

21. “ GOOD JOB!
Remember,
you are capable of amazing
things, when you set your
mind to it!
26 𝑡ℎ