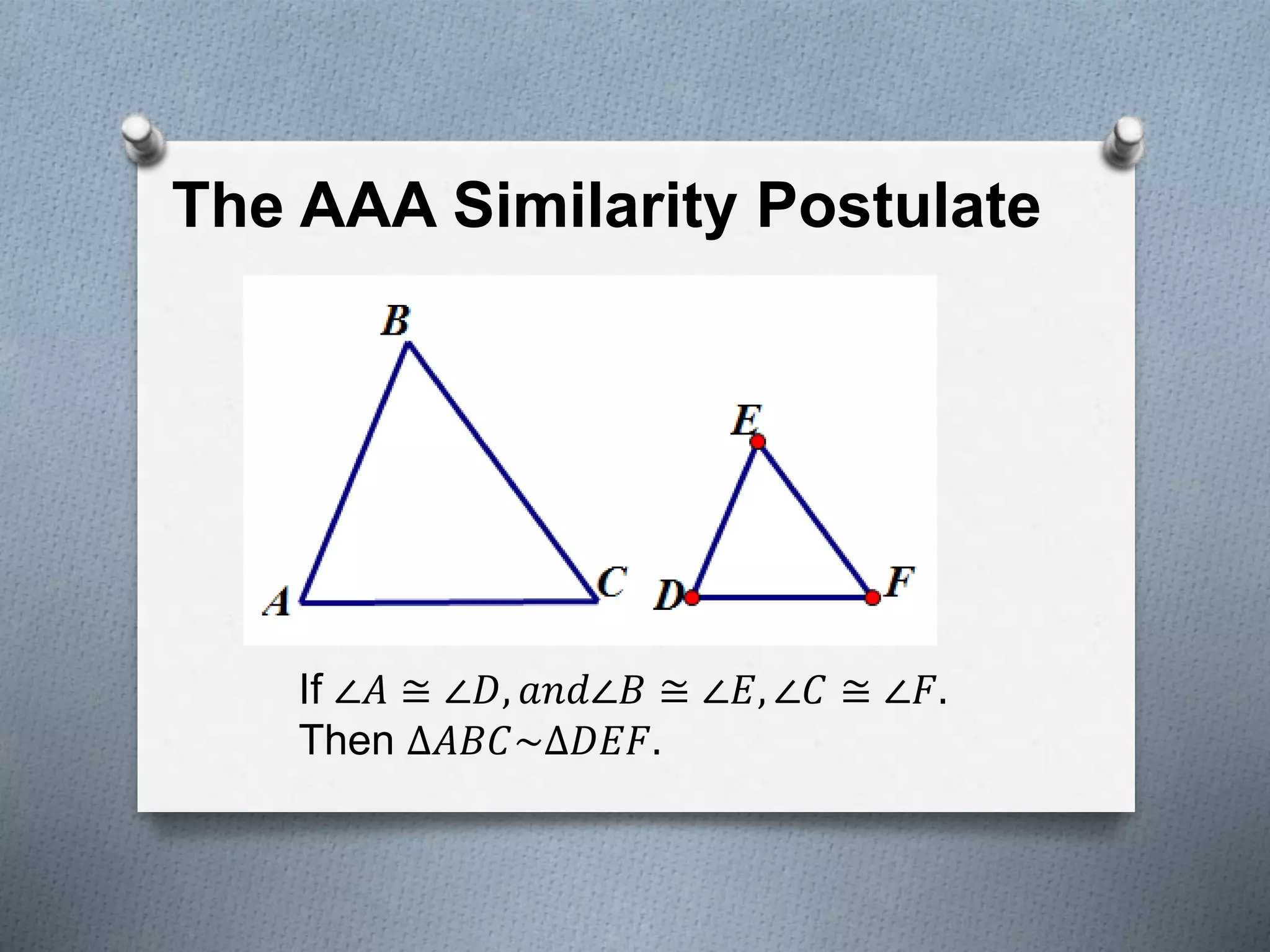
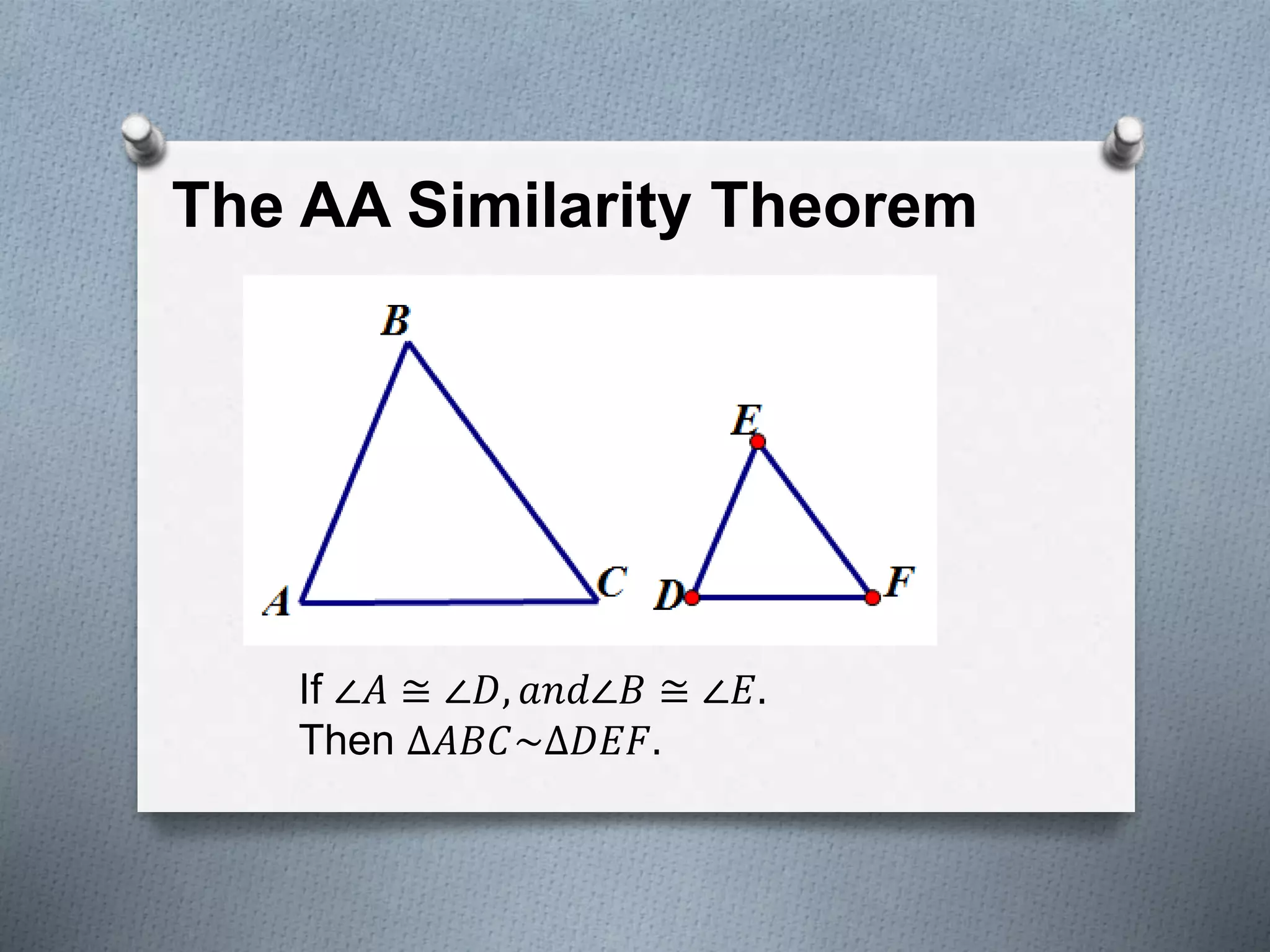
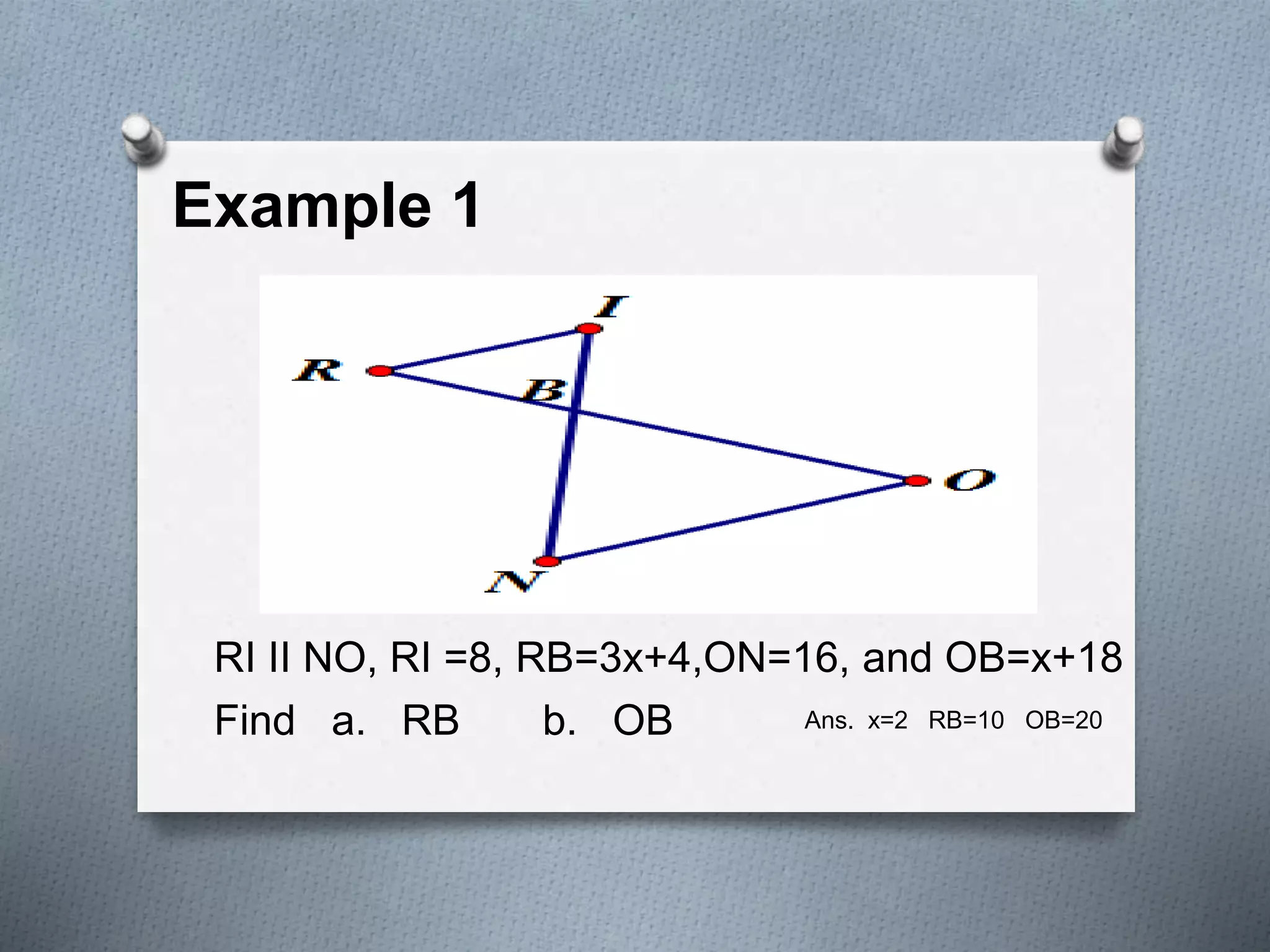
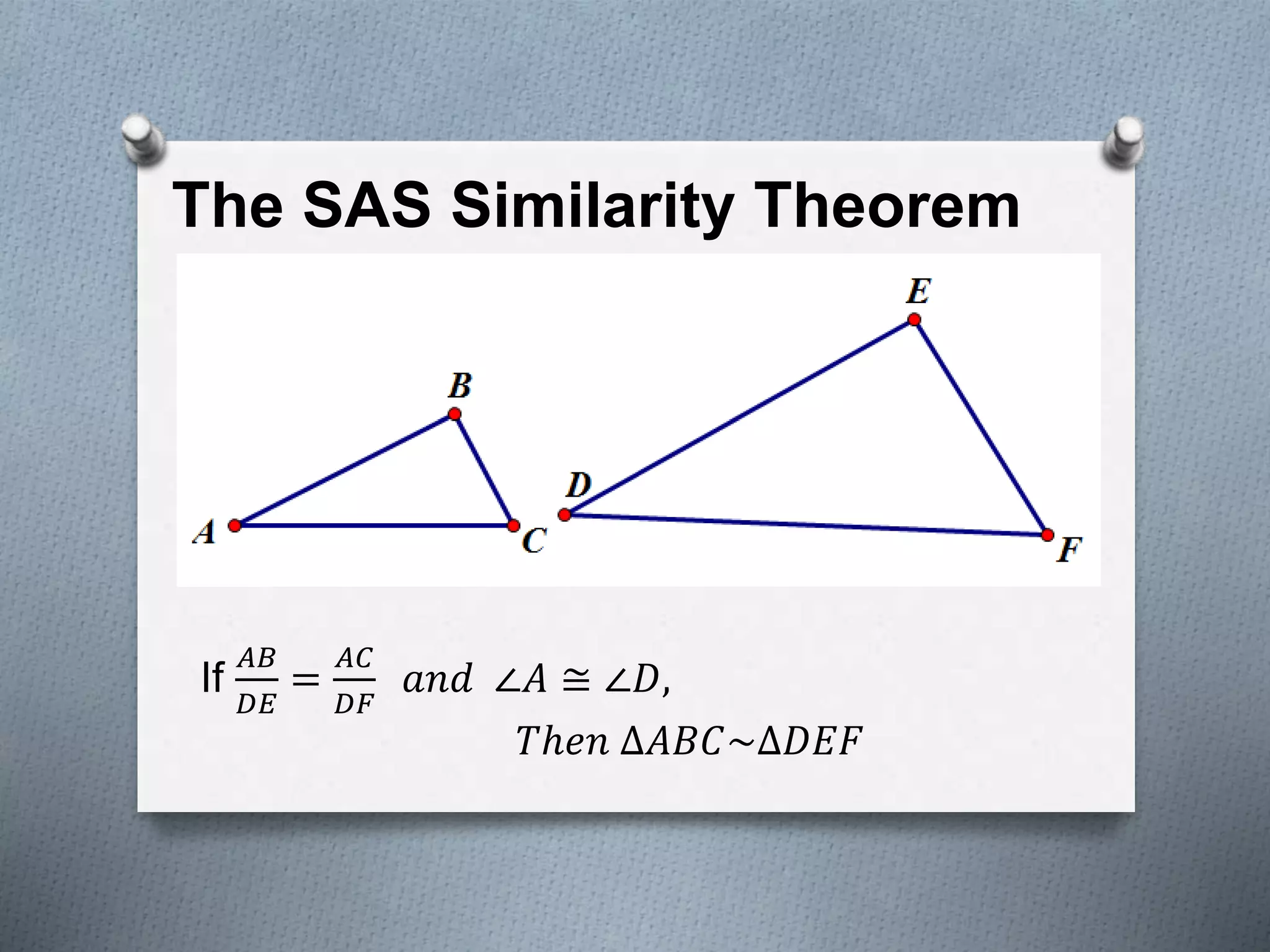
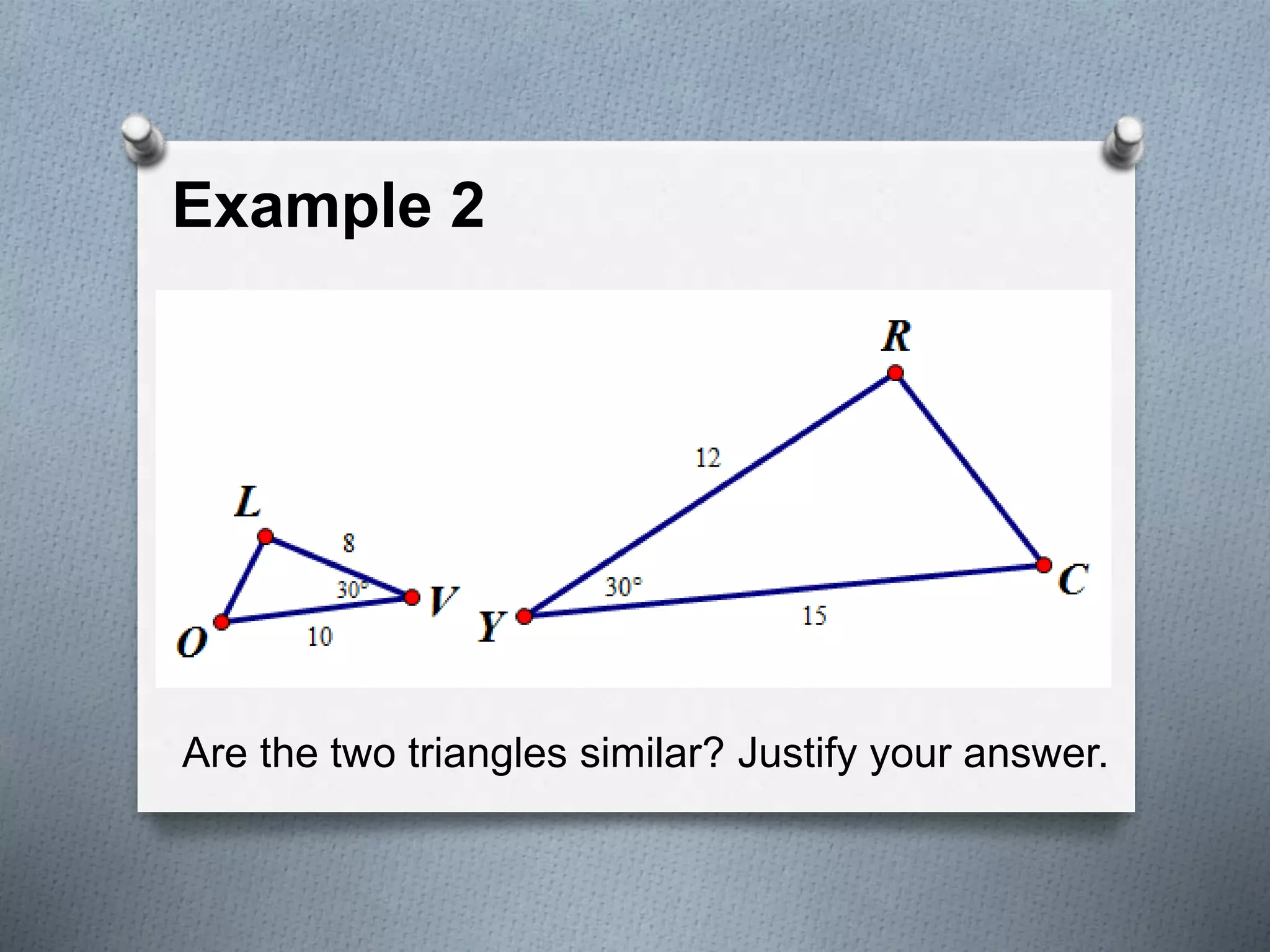
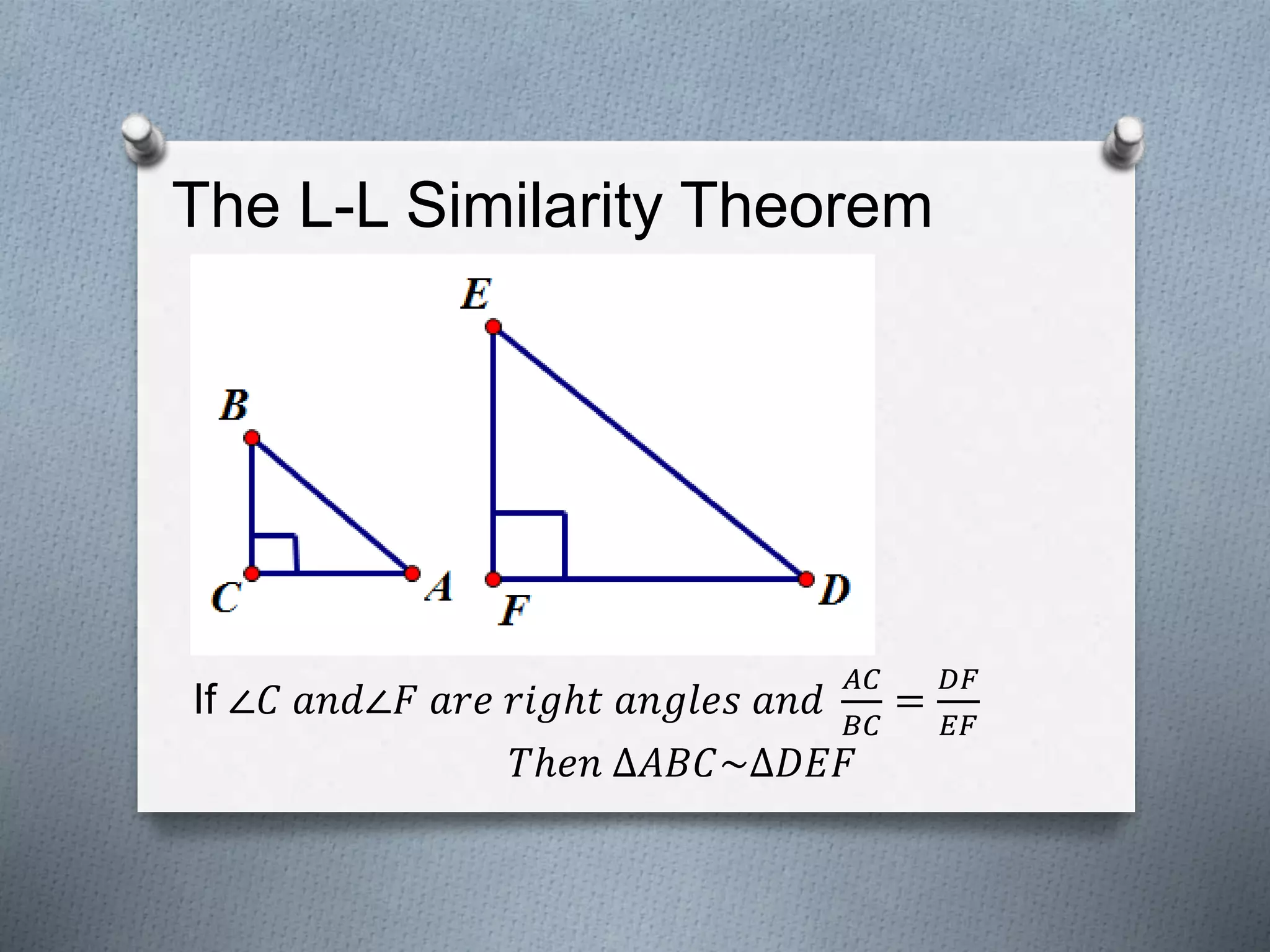
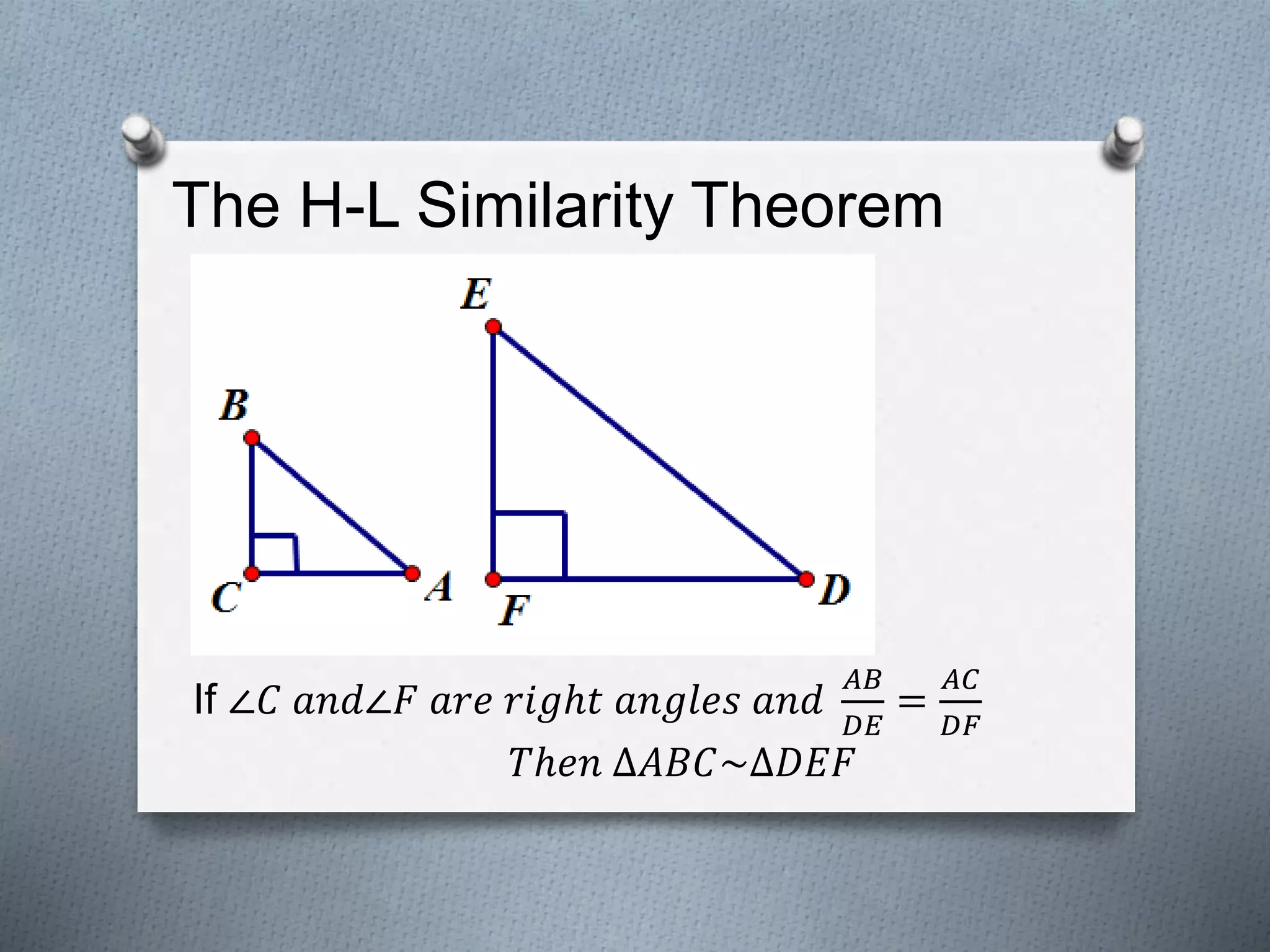
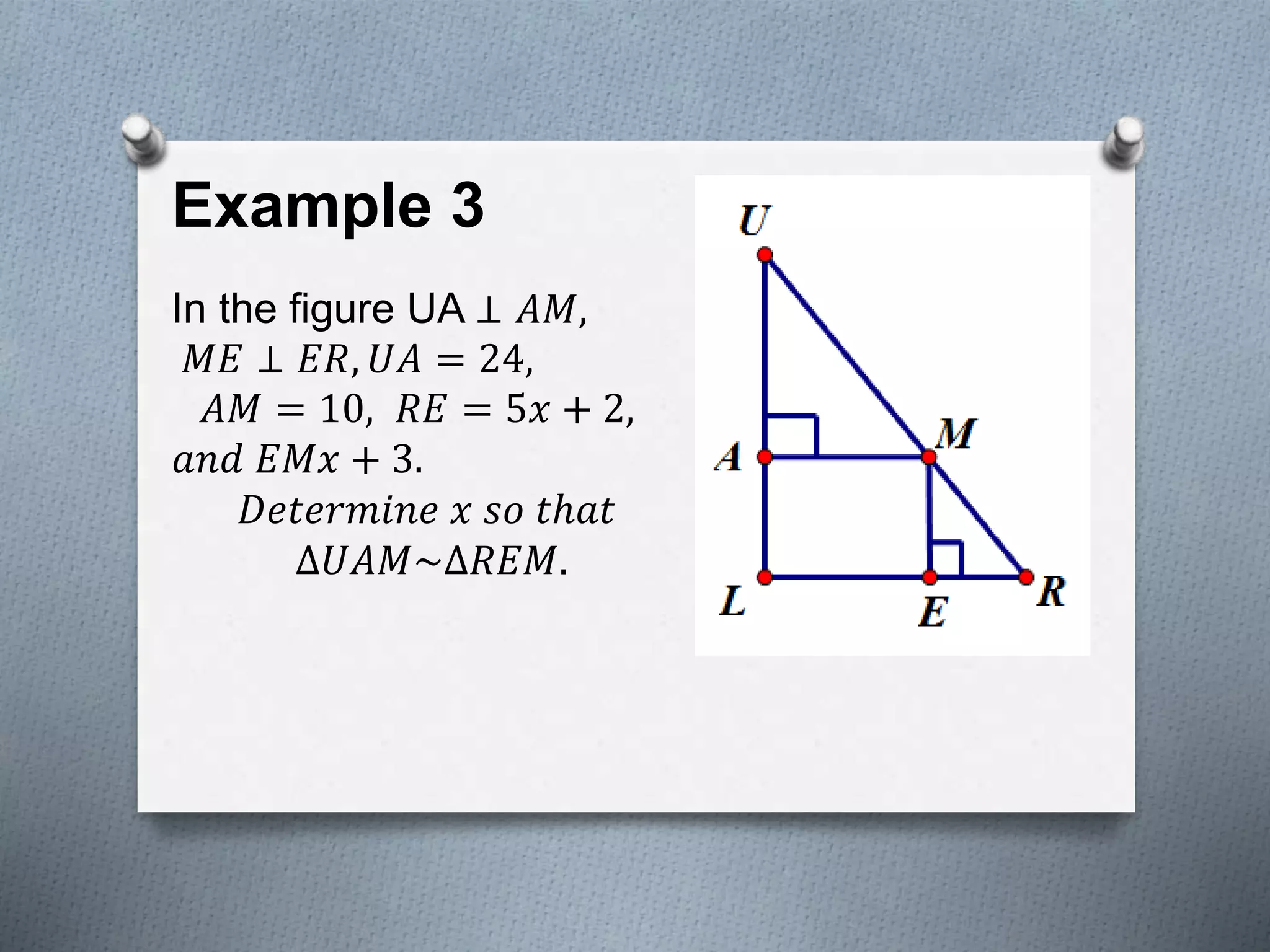
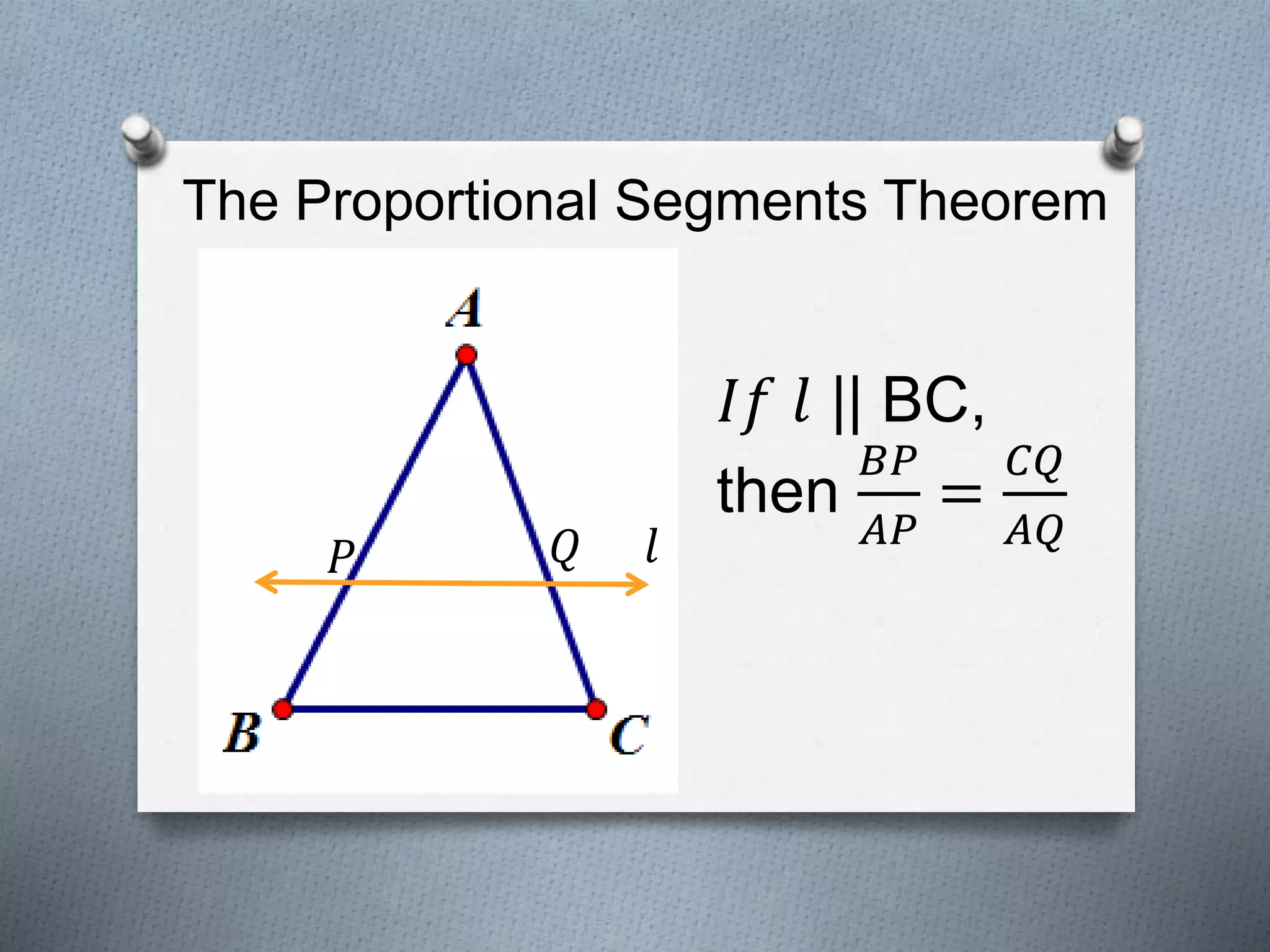
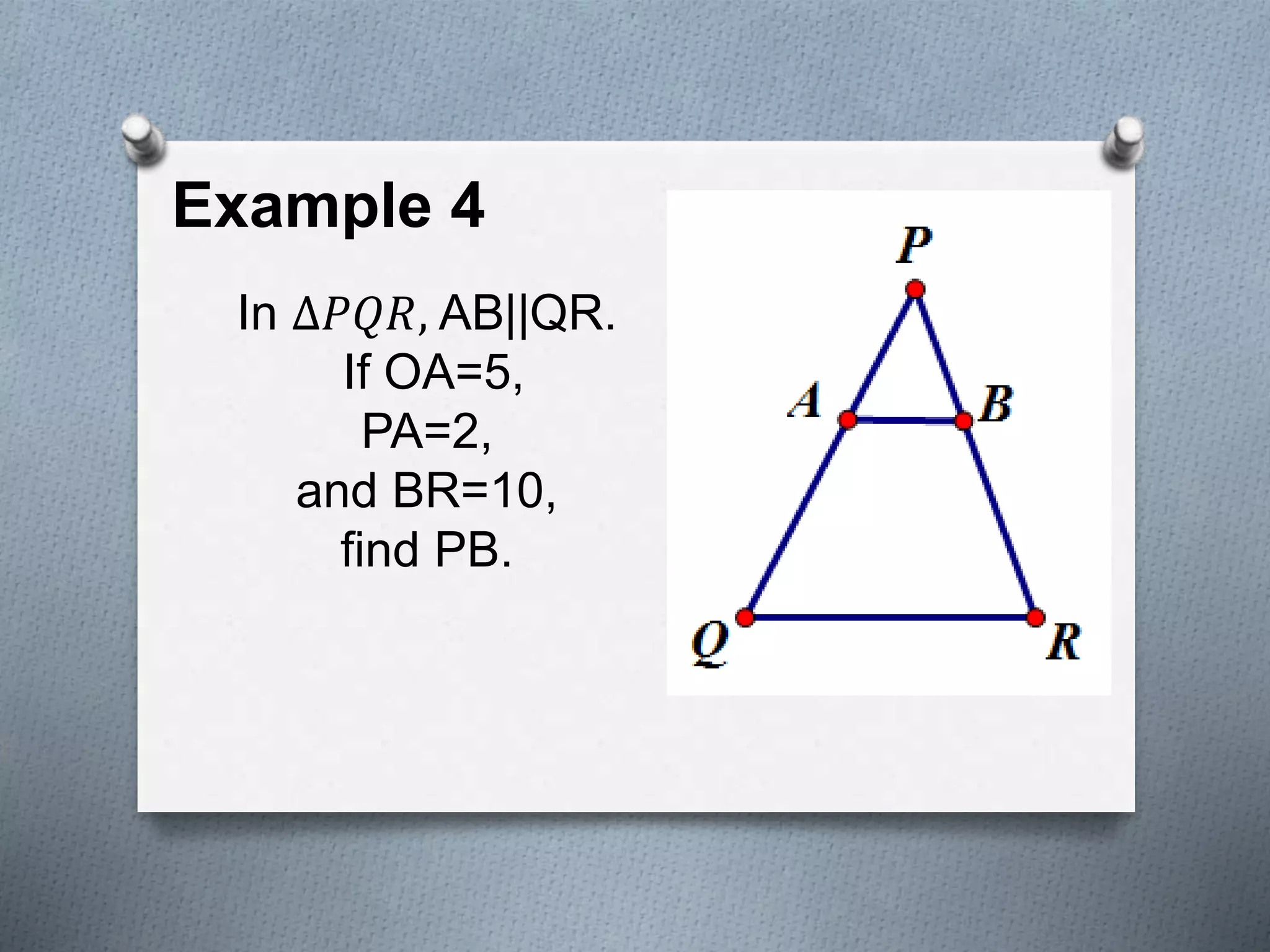
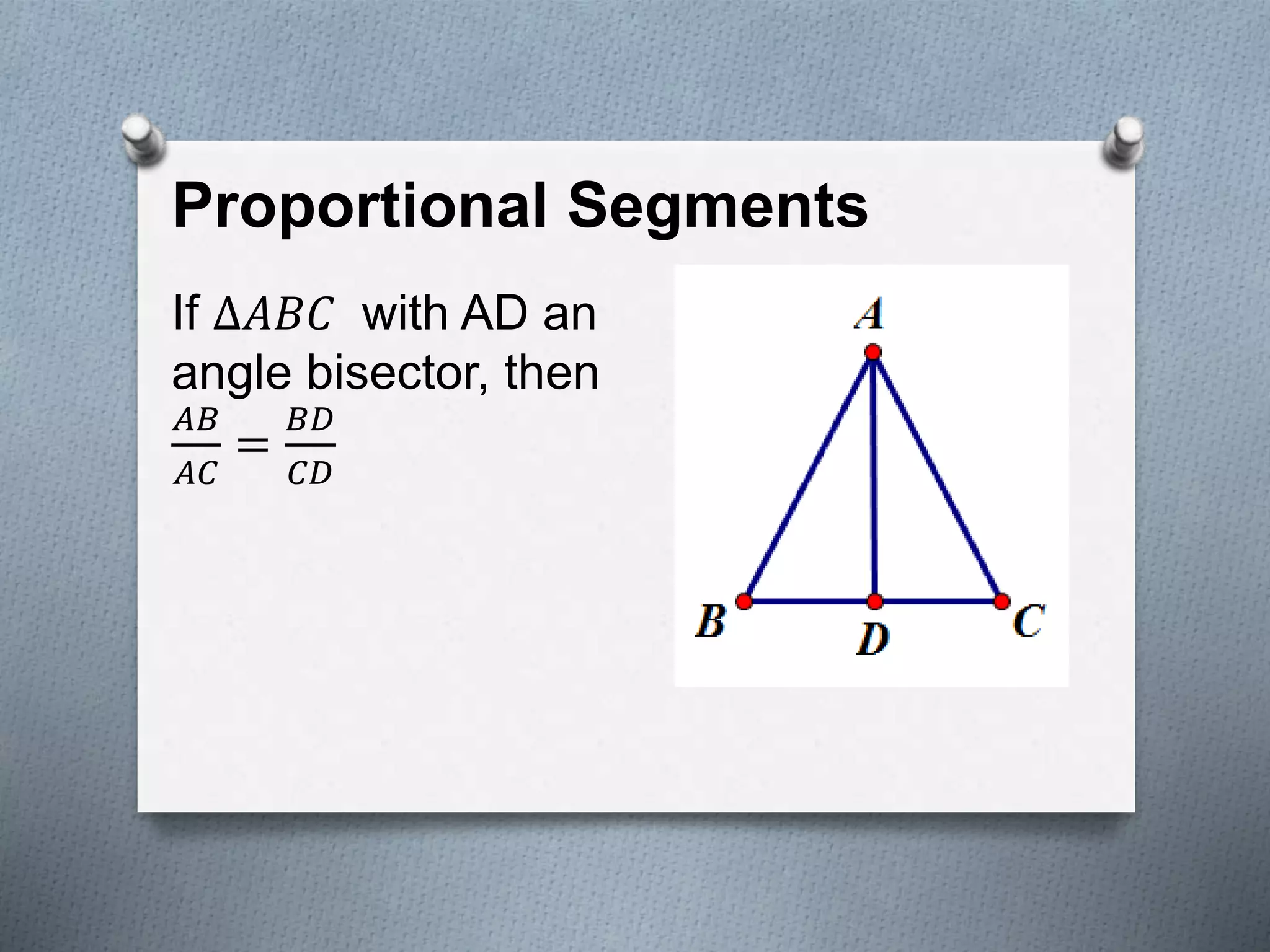
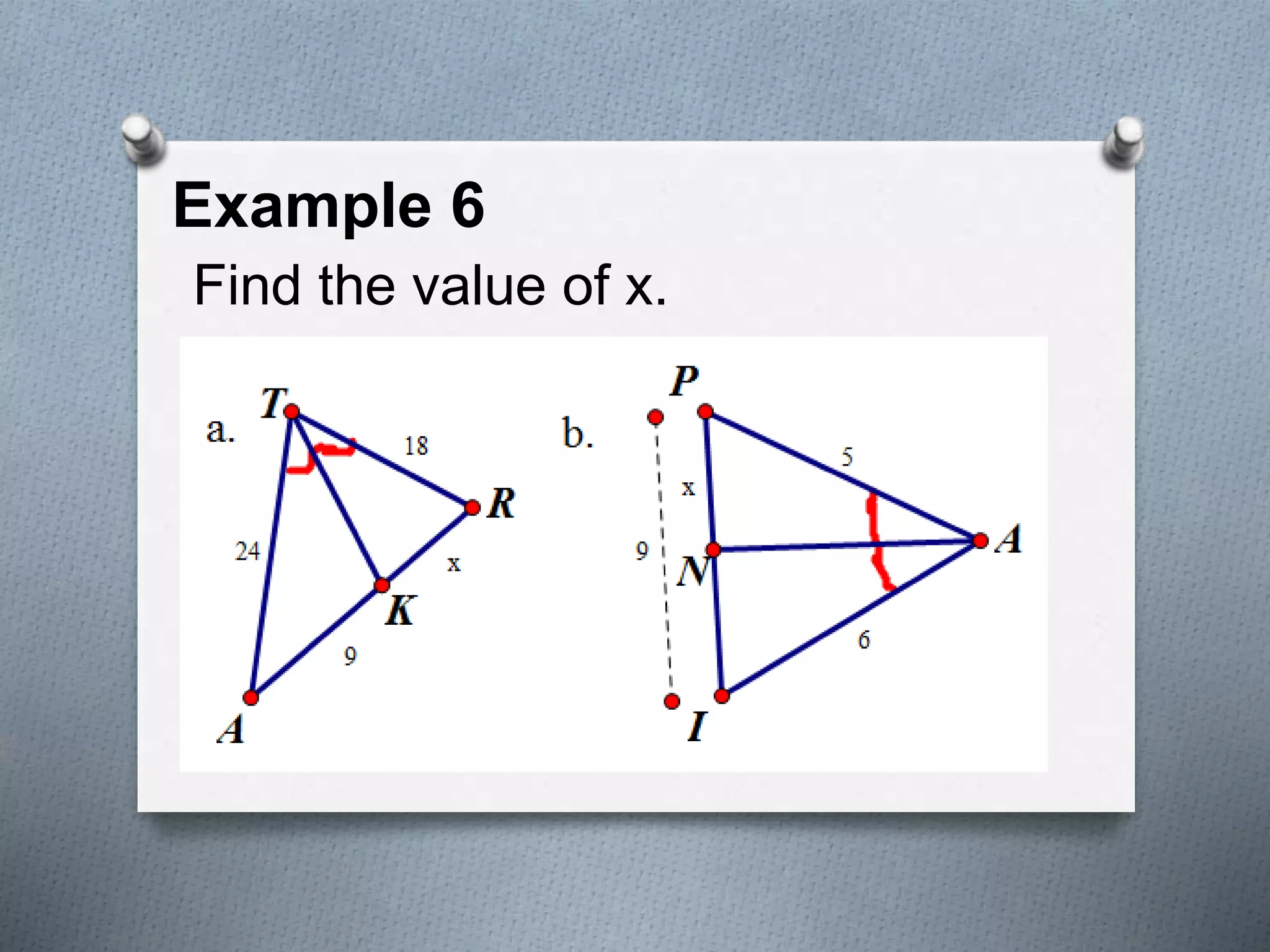
This document covers several theorems regarding similar triangles: AAA, AA, and SAS similarity theorems state that if corresponding angles or sides are proportional, the triangles are similar. The SSS and L-L theorems for right triangles also make claims of similarity based on proportional sides. Examples demonstrate applying these theorems to determine if triangles are similar and to find missing side lengths. The proportional segments theorem is also described as relating ratios of line segments cut by parallel lines.

1. Similar Triangles

2. The AAA Similarity Postulate
If three angles of one triangle are
congruent to three angle of
another triangle, then the two
triangles are similar.

3. The AAA Similarity Postulate
If ∠𝐴 ≅ ∠𝐷, 𝑎𝑛𝑑∠𝐵 ≅ ∠𝐸, ∠𝐶 ≅ ∠𝐹.
Then ∆𝐴𝐵𝐶~∆𝐷𝐸𝐹.

4. The AA Similarity Theorem
If ∠𝐴 ≅ ∠𝐷, 𝑎𝑛𝑑∠𝐵 ≅ ∠𝐸.
Then ∆𝐴𝐵𝐶~∆𝐷𝐸𝐹.

5. Example 1
RI II NO, RI =8, RB=3x+4,ON=16, and OB=x+18
Find a. RB b. OB Ans. x=2 RB=10 OB=20

6. The SAS Similarity Theorem
If two sides of one triangle are
proportional to the corresponding
two sides of another triangle and
their respective included angles
are congruent, then the triangles
are similar.

7. The SAS Similarity Theorem
If
𝐴𝐵
𝐷𝐸
=
𝐴𝐶
𝐷𝐹
𝑎𝑛𝑑 ∠𝐴 ≅ ∠𝐷,
𝑇ℎ𝑒𝑛 ∆𝐴𝐵𝐶~∆𝐷𝐸𝐹

8. Example 2
Are the two triangles similar? Justify your answer.

9. The SSS Similarity Theorem
If the sides of one triangle are
proportional to the corresponding
sides of a second triangle, then
the triangles are similar.

10. Similar right triangles
The L-L Similarity Theorem
If the legs of a right triangle are
proportional to the corresponding
legs of another right triangle, the
right triangles are similar.

11. The L-L Similarity Theorem
If ∠𝐶 𝑎𝑛𝑑∠𝐹 𝑎𝑟𝑒 𝑟𝑖𝑔ℎ𝑡 𝑎𝑛𝑔𝑙𝑒𝑠 𝑎𝑛𝑑
𝐴𝐶
𝐵𝐶
=
𝐷𝐹
𝐸𝐹
𝑇ℎ𝑒𝑛 ∆𝐴𝐵𝐶~∆𝐷𝐸𝐹

12. Similar right triangles
The H-L Similarity Theorem
If the hypotenuse and a leg of
a right triangle are proportional to
the corresponding hypotenuse
and leg of another right triangle,
then the right triangles are
similar.

13. The H-L Similarity Theorem
If ∠𝐶 𝑎𝑛𝑑∠𝐹 𝑎𝑟𝑒 𝑟𝑖𝑔ℎ𝑡 𝑎𝑛𝑔𝑙𝑒𝑠 𝑎𝑛𝑑
𝐴𝐵
𝐷𝐸
=
𝐴𝐶
𝐷𝐹
𝑇ℎ𝑒𝑛 ∆𝐴𝐵𝐶~∆𝐷𝐸𝐹

14. Example 3
In the figure UA ⊥ 𝐴𝑀,
𝑀𝐸 ⊥ 𝐸𝑅, 𝑈𝐴 = 24,
𝐴𝑀 = 10, 𝑅𝐸 = 5𝑥 + 2,
𝑎𝑛𝑑 𝐸𝑀𝑥 + 3.
𝐷𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑒 𝑥 𝑠𝑜 𝑡ℎ𝑎𝑡
∆𝑈𝐴𝑀~∆𝑅𝐸𝑀.

15. Proportional Segments
The Proportional Segments Theorem
If a line intersects two sides of a
triangle at distinct points and is
parallel to the third side, the line
divides the two sides in two
proportional segments.

16. The Proportional Segments Theorem
𝑙𝑄𝑃
𝐼𝑓 𝑙 || BC,
then
𝐵𝑃
𝐴𝑃
=
𝐶𝑄
𝐴𝑄

17. Example 4
In ∆𝑃𝑄𝑅, AB||QR.
If OA=5,
PA=2,
and BR=10,
find PB.

18. Example 5
A flagpole 8m high casts a shadow
of 12m, while a nearby building
casts a shadow of 60m. How high
is a building?

19. Proportional Segments
The Bisector of an angle of a triangle
divides the opposite side into
segments which are proportional to
the adjacent sides.

20. Proportional Segments
If ∆𝐴𝐵𝐶 with AD an
angle bisector, then
𝐴𝐵
𝐴𝐶
=
𝐵𝐷
𝐶𝐷

21. Example 6
Find the value of x.