2. รูปทัวไปของสมการเชิงเส้นสองตัวแปรคือ Ax + By + C = 0 เมือ A, B, C เป็ น
่ ่
ค่าคงตัวที่ A และ B ไม่เท่ากับศูนย์พร้อมกัน คู่อนดับ (x, y) ทีสอดคล้องกับสมการขา้ งต้น
ั ่
เป็ นคาตอบของสมการ และกราฟแสดงคาตอบของสมการเป็ นเส้นตรง
ให้ a, b, c, d, e และ f เป็ นจานวนจริงที่ a, b ไม่เป็ นศูนย์พร้อมกัน และ c, d ไม่
เป็ นศูนย์พร้อมกัน ระบบทีประกอบด้วยสมการ
่
ax + by = e
cx + dy = f
เป็ นระบบสมการเชิงเส้นสองตัวแปรทีมี x และ y เป็ นตัวแปร
่
a และ c เป็ นสัมประสิทธิ์ของ x b และ d เป็ นสัมประสิทธิ์ของ y
คาตอบของระบบสมการเชิงเส้นสองตัวแปร คือคู่อนดับ (x, y) ทีสอดคล ้องกับสมการทังสอง
ั ่ ้

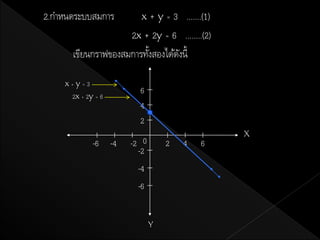
3. ตัวอย่าง 1.กาหนดระบบสมการ 3x – y = 6 .......(1)
2x + y = 4 .......(2)
เขียนกราฟของสมการทังสองได้เงนี้
้
3x – y = 6
6
4
2
(2, 0)
X
-6 -4 -2 0 2 4 6
-2
-4 2x + y = 4
-6
Y

4. จากกราฟ จะเห็นว่ามีคู่อนดับมากมายทีเ่ ป็ นตาตอบของสมการ 3x – y = 6 และสมการ
ั
2x + y = 4 มีคู่อนดับมากมายทีเ่ ป็ นคาตอบเช่นกัน
ั
เนื่องจากกราฟของสมการทังสองเป็ นเส้นตรงสองเส้นตัดกันทีจด (2, 0) เพียงจุดเดียว
้ ุ่
แสดงว่า (2, 0) เป็ นคาตอบของระบบสมการ
ดังนัน ระบบสมการนี้จงคาตอบพียงคาตอบเดียวคือ (2, 0)
้ ึ

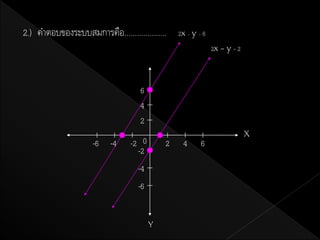
5. 2.กาหนดระบบสมการ x+y =
3 .......(1)
2x + 2y = 6 ........(2)
เขียนกราฟของสมการทังสองได้ดงนี้
้ ั
x+y=3
2x + 2y = 6
6
4
2
X
-6 -4 -2 0 2 4 6
-2
-4
-6
Y

6. จากกราฟ จะเห็นว่ามีคู่อนดับมากมายทีเ่ ป็ นคาตอบของสมการ x + y = 3 และสมการ
ั
2x + 2y = 6 มีคู่อนดับมากมายทีเ่ ป็ นคาตอบเช่นกัน
ั
เนื่องจากกราฟของสมการทังสองเป็ นเส้นตรงสองเส้นทีทบกัน แสดงว่าคู่อนดับทุกคู่ม่ี
้ ่ ั ั
เป็ นพิกดของจุดบนเส้นตรงทีทบกันนี้ เป็ นคาตอบของระบบสมการ
ั ่ ั
ดังนัน ระบบสมการนี้จงมีคาตอบมากมายไม่จากัด
้ ึ

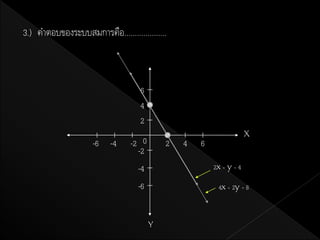
7. 3.กาหนดระบบสมการ 2x – 3y = 6
2x = 3y – 12
เขียนกราฟของสมการทังสองได้ดงนี้
้ ั
2x - 3y = 6
6
4 2x = 3y - 12
2
X
-6 -4 -2 0 2 4 6
-2
-4
-6
Y

8. จากกราฟ จะเห็นว่ามีคู่อนดับมากมายทีเ่ ป็ นคาตอบของสมการ 2x – 3y = 6 และสมการ
ั
2x = 3y – 12 มีคู่อนดับมากมายทีเ่ ป็ นคาตอบเช่นกัน
ั
เนื่องจากกราฟของสมการทังหมดเป็ นเส้นสองเส้นขนานกัน จึงไม่มคู่อนดับใดเป็ นคาตอบ
้ ี ั
ของสมการทังสอง
้
ดังนัน ระบบสมการนี้จงไม่มคาตอบ
้ ึ ี
จากตัวอย่างข้างต้น ระบบสมการเชิงเส้นสองตัวแปรอาจมีคาตอบเดียว มีหลายคาตอบ
หรือไม่มคาตอบเลยก็ได้
ี

9. แบบฝึ กหัดที่ 3.1
ให้นกเรียนพิจารณาว่าระบบสมการมีคาตอบหรือไม่ ถ้ามีคาตอบเดียว ให้ระบุคาตอบด้วย
ั
1.) คาตอบของระบบสมการคือ....................
x + 3y = 9 6
4
2
X
-6 -4 -2 0 2 4 6
-2
-4
x + 3y = -3
-6
Y

10. 2.) คาตอบของระบบสมการคือ.................... 2x - y - 6
2x - y = 2
6
4
2
X
-6 -4 -2 0 2 4 6
-2
-4
-6
Y

11. 3.) คาตอบของระบบสมการคือ....................
6
4
2
X
-6 -4 -2 0 2 4 6
-2
-4 2x + y = 4
-6 4x + 2y = 8
Y

12. เฉลย : แบบฝึ กหัดที่ 3.1
1. (3, 2)
2. ไม่มคาตอบ
ี
3. มีไม่จากัด

13. การแก้สมการเป็ นการหาคาตอบของสมการ การหาคาตอบของสมการเชิงเส้นสองตัวแปร
นอกจากใช้กราฟแลว ยังใช้สมบัตการเท่ากัน เช่น สมบัตสมมาตร สมบัตการถ่ายทอด
้ ิ ิ ิ
สมบัตการบวก และสมบัตการคูณ
ิ ิ

14. ตัวอย่างที่ 1 จงแก้ระบบสมการ 3x – y = 9
2x + y = 6
วิธทา
ี 3x – y = 9 .......(1)
2x + y = 6 .......(2)
(1) + (2) : (3x – y) + (2x + y = 6) = 9 + 6
5x = 15
1 x 5x = 1 x 15
5 5
x=3
แทนค่า x = 3 ใน (2) เพือหาค่าของ y
่
2(3) + y = 6
6+y=6

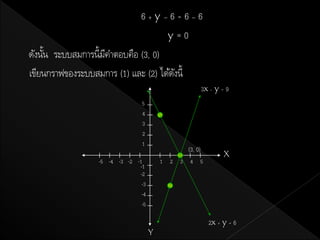
15. 6+y–6=6–6
y=0
ดังนัน ระบบสมการนี้มคาตอบคือ (3, 0)
้ ี
เขียนกราฟของระบบสมการ (1) และ (2) ได้ดงนี้
ั
3x - y = 9
5
4
3
2
1
(3, 0)
X
-5 -4 -3 -2 -1 1 2 3 4 5
-1
-2
-3
-4
-5
2x + y = 6
Y

16. เนื่องจากกราฟของสมการ (1) และ (2) เป็ นเส้นตรงสองเส้น ตัดกันทีจด (3, 0)
ุ่
ดังนัน ระบบสมการนี้มคาตอบเพียงคาตอบเดียวคือ (3, 0)
้ ี
ตัวอย่างที่ 2 จงแก้ระบบสมการ 2x + y = 3
6x + 3y = -12
วิธทา
ี 2x + y = 3
6x + 3y = -12
(1) x 3 : 6x + 3y = 9
(2) - (3) : (6x + 3y) - (2x + y) = -12 -9
6x + 3y - 6x + 3y = -21
0 = -21 ซึงเป็ นสมการทีไม่เป็ นจริง
่ ่
ไม่สามารถหาค่า x และค่า y ทีทาให้สมการเป็ นจริง
่

17. ดังนันระบบสมการนี้ไม่มคาตอบ
้ ี
เขียนกราฟของระบบสมการ (1) และ (2) ได้ดงนั้
ั
4
3
2
1
X
-4 -3 -2 -1 0 1 2 3 4
-1
-2
-3 2x + y = 3 .......(1)
-4
6x + 3y = -12 .......(2)
Y

18. เนื่องจากกราฟของ (1) และกราฟของ (2) เป็ นเส้นตรงซึงขนานกัน จึงไม่มจดตัด
่ ีุ
ดังนัน ระบบสมการนี้ไม่มคาตอบ
้ ี
ตัวอย่างที่ 3 จงแก้ระบบสมการ x – 2y = -1
-2x + 4y = 2
วิธทา
ี x - 2y = -1 ..........(1)
-2x + 4y = 2 ...........(2)
(2) (-2) : x – 2y = -1 ............(3)
..
จะเห็นว่า สมการ (3) ทีได้จากสมการ (2) เป็ นสมการเดียวกับสมการ (1) แสดงว่า
่
สมการ (1) และสมการ (2) มีคาตอบเป็ นอย่างเดียวกัน ซึงมีมากมายไม่จากัด
่
ดังนัน คู่อนดับทีเ่ ป็ นคาตอบของระบบสมการนี้ได้จากสมการ (1) หรือสมการ (2)
้ ั
จาก (1) : x – 2y = -1
x + 1 = -1

19. x 1
y
+
=
2
ดังนัน ระบบสมการนี้มคาตอบมากมายไม่จากัดในรูป (x, x + 1 )
้ ี
2
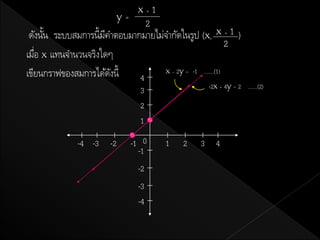
เมือ x แทนจานวนจริงใดๆ
่
เขียนกราฟของสมการได้ดงนี้
ั x 2y -1 .......(1)- =
4
-2x + 4y = 2 .......(2)
3
2
1
-4 -3 -2 -1 0 1 2 3 4
-1
-2
-3
-4

20. เนื่องจากสมการ x – 2y = -1 และกราฟของสมการ -2x + 4y = 2 เป็ นเส้นตรงทับ
กัน
ดังนัน ระบบสมการนี้จงมีคาตอบมากมายไม่จากัด
้ ึ
คาตอบของระบบสมการมีมากมายไม่จากัดอยู่ในรูป (, x + 1 )
2
เมือ x แทนจานวนจริงใดๆ
่

21. แบบฝึ กหัดที่ 3.2
ให้นกรยนแก้ระบบสมการเชิงเส้นสองตัวแปรต่อไปนี้
ั ้ี
1.) x+y=4 ........(1)
x–y=0 .......(2)
(1) + (2) : 2x = ..........
x = ..........
แทนค่า x ใน (1)
...... + y = ..........
y = ..........
ระบบสมการนี้มคาตอบคือ...............................
ี

22. 2.) x+y = -4 ........(1)
y–x=2 .......(2)
(1) + (2) : .................
.................
แทนค่า x ใน (1) :
x + ...... = ..........
x = ..........
ระบบสมการนี้มคาตอบคือ...............................
ี

23. เฉลย : แบบฝึ กหัดที่ 3.2
1.) x+y = 4 ........(1)
x–y=0 .......(2)
(1) + (2) : 2x = 4
x=2
แทนค่า x ใน (1)
2+y=4
y=2
ระบบสมการนี้มคาตอบคือ.....(2, 2).....
ี

24. 2.) x+y = -4 ........(1)
y–x=2 .......(2)
(1) + (2) : 2y = -2
y = -1
แทนค่า x ใน (1) :
x + (-1) = -4
x = -3
ระบบสมการนี้มคาตอบคือ.....(-3, -1).....
ี

25. ตัวอย่างที่ 1 จานวนสองจานวนรวมกันเป็ น 7 และผลต่างของจานวนนันเป็ น 5 จงหาจานวน
้
ทังสอง
้
วิธทา ให้จานวนทีมากกว่าเป็ น x
ี ่
และจานวนทีนอยกว่าเป็ น y
่ ้
จานวนสองจานวนนันเป็ น 7 เขียนสมการได้ดงนี้
้ ั
x+y=7 ...........(1)
ผลต่างของสองจานวนนันเป็ น 5 เขียนสมการได้ดงนี้
้ ั
x–y=5 ...........(2)

26. ดาเนินการแก้สมการหาค่าของ x และ y
(1) + (2) : 2x = 12
x=6
(1) - (2) : 2y = 2
y=1
ตรวจสอบ ถ้าจานวนทังสองคือ 6 และ 1
้
จะมีผลบวกเป็ น 6 + 1 = 7
และผลต่างเป็ น 6 - 1 = 5
ดังนัน จานวนทังสองคือ 6 และ 1
้ ้
ตอบ 6 และ 1

27. แบบฝึ กหัดที่ 3.3
1. จงหาจานวนสองจานวนซึงรวมกันเป็ น 136 และต่างกัน 42
่
วิธทา ให้จานวนทีมากกว่าเป็ น x
ี ่
และจานวนทีนอยกว่าเป็ น y
่ ้
จานวนสองจานวนรวมกันเป็ น 136 เขียนสมการได้ดงนี้ ั
x + y = .............
จานวนสองจานวนต่างกัน 42 เขียนสมการได้ดงนี้ ั
.............................
(1) + (2) : .....................................................................
...........................................................................

28. แทนค่า x = ....... ใน (1) จะได้
..........................................................................................
..........................................................................................
..........................................................................................
ตรวจสอบ ผลบวกของจานวนทังสองคือ ............................................
้
ผลลบของจานวนทังสองคือ ..............................................
้
.........................................................................................
.........................................................................................

29. เฉลย : แบบฝึ กหัดที่ 3.3
1. จงหาจานวนสองจานวนซึงรวมกันเป็ น 136 และต่างกัน 42
่
วิธทา ให้จานวนทีมากกว่าเป็ น x
ี ่
และจานวนทีนอยกว่าเป็ น y
่ ้
จานวนสองจานวนรวมกันเป็ น 136 เขียนสมการได้ดงนี้ั
x + y = 136
จานวนสองจานวนต่างกัน 42 เขียนสมการได้ดงนี้ ั
x – y = 42
(1) + (2) : 2x = 178
x = 89

30. แทนค่า x = 89 ใน (1) จะได้
89 + y = 136
y = 47
ตรวจสอบ ผลบวกของจานวนทังสองคือ 136
้
ผลลบของจานวนทังสองคือ 47
้
ดังนัน จานวนทังสองคือ 136 และ 47
้ ้
ตอบ 136 และ 47

31. 1.เฉลิมพร แก้วนอก (22)
2.ณัฏชนก หาญอยู่คม (23)
ุ้
3.นัทมล นุ่มนาค (25)
4.พสุพร กุลภัทรวิจตร (28)
ิ