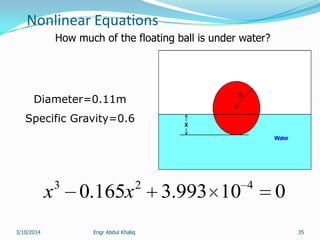
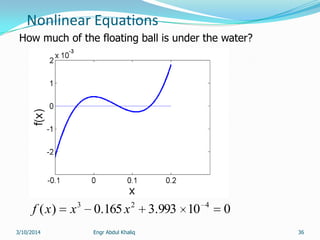
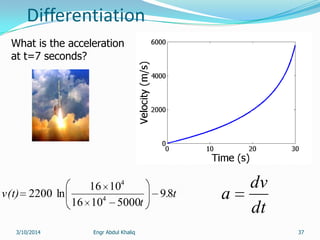
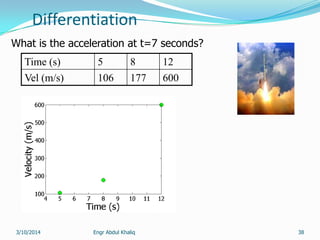
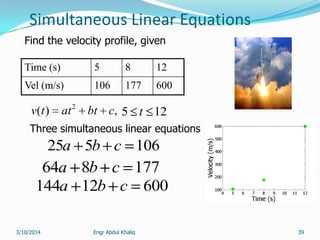
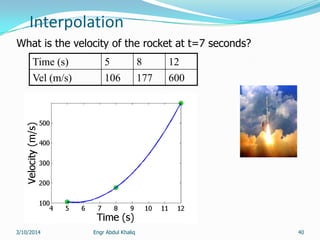
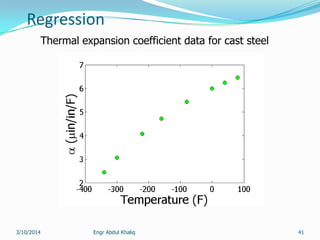
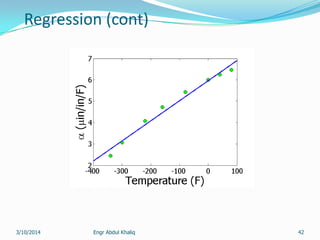
The document outlines a course on numerical methods within the context of engineering, focusing on programming proficiency, structured techniques, and various mathematical concepts like interpolation, eigenvalues, and the solution of differential equations. It emphasizes error propagation, sources of numerical errors such as round-off and truncation errors, and includes examples illustrating these concepts. The course includes practical programming assignments and a list of suggested readings for students.


























![30
Example 3 — Integration
Use two rectangles of equal width to
approximate the area under the curve for
2
)( xxf over the interval ]9,3[
y = x 2
0
30
60
90
0 3 6 9 12
y
x
9
3
2
dxx
Engr Abdul Khaliq3/10/2014](https://image.slidesharecdn.com/id-302lecture1-140310072630-phpapp01/85/Engineering-Numerical-Analysis-Lecture-1-30-320.jpg)