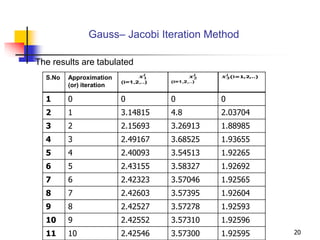
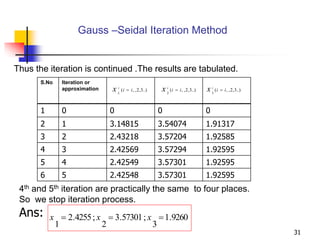
The document discusses two iterative methods for solving systems of linear equations: Gauss-Jacobi and Gauss-Seidel. Gauss-Jacobi solves each equation separately using the most recent approximations for the other variables. Gauss-Seidel updates each variable with the most recent values available. The document provides an example applying both methods to solve a system of three equations. Gauss-Seidel converges faster, requiring fewer iterations than Gauss-Jacobi to achieve the same accuracy. Both methods are useful alternatives to direct methods like Gaussian elimination when round-off errors are a concern.

1. 1
 Gauss – Jacobi Iteration Method
 Gauss - Seidal Iteration Method

2. Iterative Method
 Simultaneous linear algebraic equation occur in various fields of Science
and Engineering.
 We know that a given system of linear equation can be solved by
applying Gauss Elimination Method and Gauss – Jordon Method.
 But these method is sensitive to round off error.
 In certain cases iterative method is used.
 Iterative methods are those in which the solution is got by successive
approximation.
 Thus in an indirect method or iterative method, the amount of
computation depends on the degree of accuracy required.
2
Introduction:

3. Iterative Method
 Iterative methods such as the Gauss – Seidal method give the user
control of the round off.
 But this method of iteration is not applicable to all systems of equation.
 In order that the iteration may succeed, each equation of the system
must contain one large co-efficient.
 The large co-efficient must be attached to a different unknown in that
equation.
 This requirement will be got when the large coefficients are along the
leading diagonal of the coefficient matrix.
 When the equation are in this form, they are solvable by the method of
successive approximation.
 Two iterative method - i) Gauss - Jacobi iteration method
ii) Gauss - Seidal iteration method
3
Introduction (continued..)

4. Gauss – Jacobi Iteration Method:
The first iterative technique is called the Jacobi method named after
Carl Gustav Jacob Jacobi(1804- 1851).
Two assumption made on Jacobi method:
1)The system given by
4

a x  a x   a x 
b
- - - - - - - - (1)
11 1 12 2 1 n n
1 
a x  a x   a x 
b
n n
21 1 22 2 2 2


a x  a x   a x 
b
n 1 1 n 2 2
nn n n
- - - - - - - - (2)
- - - - - - - - (3)
has a unique solution.

5. Gauss – Jacobi Iteration Method
5
Second assumption:
3 7 13 76 1 2 3 x  x  x 
5 3 28 1 2 3 x  x  x 
12 3 0 1 1 2 3 x  x  x 
12 3 0 1 1 2 3 x  x  x 
5 3 28 1 2 3 x  x  x 
3 7 13 76 1 2 3 x  x  x 

6. Gauss– Jacobi Iteration Method
6

ij a a
j 
1


n
j
i
ii

7. To begin the Jacobi method ,solve

7
Gauss– Jacobi Iteration Method

a x  a x   a x 
b
n n
11 1 12 2 1 1

a x  a x   a x 
b
n n
21 1 22 2 2 2


a x  a x   a x 
b
n 1 1 n 2 2
nn n n

8. Gauss– Jacobi Iteration Method

(7)
8

9. Gauss– Jacobi Iteration Method

8
9

10. Gauss– Jacobi Iteration Method

9
10

11. 11
Gauss– Jacobi Iteration Method

12. Gauss– Jacobi Iteration Method
12

a x  a x   a x 
b
- - - -(1)
11 1 12 2 1 n n
1 
a x  a x   a x 
b
n n
21 1 22 2 2 2


a x  a x   a x 
b
n 1 1 n 2 2
nn n n
- - - -(2)
- - - -(3)

13. Gauss– Jacobi Iteration Method
13

14. Gauss– Jacobi Iteration Method
14

15. Gauss– Jacobi Iteration Method
15

16. Gauss– Jacobi Iteration Method
Solution:
In the given equation , the largest co-efficient is attached to a
different unknown.
Checking the system is diagonally dominant .
Here
Then system of equation is diagonally dominant .so iteration method
can be applied.
16
27 27 6 1 7 11 12 13 a    a  a   

17. Gauss– Jacobi Iteration Method
From the given equation we have
17
85 6 2 3
27
1
x x
x
 

72 6 2 1 3
15
2
x x
x
 

110 1 2
54
3
x x
x
 

(1)

18. Gauss– Jacobi Iteration Method
18
(1) 85  6(0) 
(0)
1
27
x 
72 6(0) 2(0)
(1)  
x 
15
2
(1)  
x 
110 (0) (0)
54
3
=3.14815
=4.8
=2.03704
First approximation

19. Gauss– Jacobi Iteration Method
19

20. Gauss– Jacobi Iteration Method
The results are tabulated
20
S.No Approximation
(or) iteration
1 0 0 0 0
2 1 3.14815 4.8 2.03704
3 2 2.15693 3.26913 1.88985
4 3 2.49167 3.68525 1.93655
5 4 2.40093 3.54513 1.92265
6 5 2.43155 3.58327 1.92692
7 6 2.42323 3.57046 1.92565
8 7 2.42603 3.57395 1.92604
9 8 2.42527 3.57278 1.92593
10 9 2.42552 3.57310 1.92596
11 10 2.42546 3.57300 1.92595

21. Gauss– Jacobi Iteration Method
21

22. Gauss –Seidal Iteration Method
 Modification of Gauss- Jacobi method,
named after Carl Friedrich Gauss and Philipp Ludwig Von Seidal.
 This method requires fewer iteration to produce the same degree
of accuracy.
 This method is almost identical with Gauss –Jacobi method except
in considering the iteration equations.
 The sufficient condition for convergence in the Gauss –Seidal
method is that the system of equation must be strictly diagonally
dominant
22

23. Gauss –Seidal Iteration Method
Consider a system of strictly diagonally dominant equation as
23

a x  a x   a x 
b
n n
11 1 12 2 1 1

a x  a x   a x 
b
n n
21 1 22 2 2 2


a x  a x   a x 
b
n 1 1 n 2 2
nn n n
- - - - -(1)
- - - - - (2)
- - - - - (3)

24. Gauss –Seidal Iteration Method
24

25. Gauss –Seidal Iteration Method

25

26. Gauss –Seidal Iteration Method
26
The successive iteration are generated by the scheme called
iteration formulae of Gauss –Seidal method are as
The number of iterations k required depends upon the desired
degree of accuracy

27. Gauss –Seidal Iteration Method
Soln: From the given equation ,we have
- - - - - - - (1)
- - - - - - -(2)
- - - - - - - (3)
27
85 6 2 3
27
1
x x
x
 

72 6 2 1 3
15
2
x x
x
 

110 1 2
54
3
x x
x
 


28. Gauss –Seidal Iteration Method
28
1.91317
85 6(0) (0)
72 6(3.14815) 2(0)
110 (3.14815) (5.54074)
54
(2)
(1)
(1)
3

 
x 
3.14815
27
1

 
x 
3.54074
15
2

 
x 

29. Gauss –Seidal Iteration Method
1st Iteration:
29
1.91317
(1)
(1)
(1)
3
3.54074
2
3.14815
1



x
x
x

30. Gauss –Seidal Iteration Method
30
For the second iteration,
1.91317
(1)
(1)
(1)
3
3.54074
2
3.14815
1



x
x
x
2.43218
(1)
(2) 
27
85 6
(1)
3
2
1
 

x x
x
3.57204
(2)
72 6 2
(2) 
15
(1)
3
1
2
 

x x
x
1.92585
(2)
(2) 
54
110
(2)
2
1
3
 

x x
x

31. Gauss –Seidal Iteration Method
Thus the iteration is continued .The results are tabulated.
S.No Iteration or
approximation
x i  ( , ,2,3..)
x i i  i x i ( i 
i , ,2,3..)
1 0 0 0 0
2 1 3.14815 3.54074 1.91317
3 2 2.43218 3.57204 1.92585
4 3 2.42569 3.57294 1.92595
5 4 2.42549 3.57301 1.92595
6 5 2.42548 3.57301 1.92595
31
(i i, ,2,3..)
1,
2
3
4th and 5th iteration are practically the same to four places.
So we stop iteration process.
Ans: x  x  x 
1.9260
3
3.57301;
2
2.4255;
1

32. Gauss –Seidal Iteration Method
Comparison of Gauss elimination and Gauss- Seidal Iteration methods:
 Gauss- Seidal iteration method converges only for special systems of
equations. For some systems, elimination is the only course
available.
 The round off error is smaller in iteration methods.
 Iteration is a self correcting method
32