The chapter discusses numerical methods for solving the 1D and 2D heat equation. Four methods are described for the 1D equation: Schmidt, Crank-Nicolson, iterative (Jacobi and Gauss-Seidel), and Du Fort-Frankel. The Schmidt method is explicit but conditionally stable, while Crank-Nicolson is implicit and unconditionally stable. Examples are solved using each method and compared to analytical solutions. The alternating direction explicit (ADE) method is described for the 2D equation.

1. 21
CHAPTER FOUR
Results and discussion:
The heat equation is an parabolic partial differential equation that
describes of the distribution of heat (or variation in temperature) in a
given region over time. In this chapter we have discussed finite difference
method such as (Schmidt method, Crank-Nicolson method, Iterative
method, and Du Fort Frankle method) for one dimensional heat
equation and, (ADE) method for two dimensional heat equation.
The equation (4.1) is given below, for one dimensional heat equation
(4.1)
Where ⁄ is the diffusivity of the substance ( ⁄ )
= constants
x = distance
t = temperature
k = coefficient of conductivity
= density of material
s = specific heat

2. 22
(1). Schmidt method: (explicit formula).
Conceders a rectangular mesh in the x-t plane with spacing along
direction and along time t direction. Denoting a mesh point ( )
( ) as simply we have,
And
Substituting these in (4.1), we obtain
= [ ]
Or = ( ) (4.2)
Where ⁄ This formula enable us
to determine the value of u at the ( ) mesh point in terms of the
known function values at the point and at the instant it is a
relation between the function values at the time levels and and is
therefore called a 2-level formula in schematic form (4.2) is shown in
fig. (4.1).

3. 23
( ) ( ) level
level
( ) ( ) ( )
Hence (4.2) is called the Schmidt explicit formula which is valid only for
0 < .
Remark. In particular when equation (4.2) reduces to
( ) ( )
Which shows that the value of at at time is the mean of the
-value at and at time . This known as bender-Schmidt
recurrence relation, gives the values of at the internal mesh points with
the help of boundary condition.
Example: 1
Use bender –Schmidt formula to solve the heat equation
With the conditions ( ) ( ) ( )
Setting we see that when
Solution:
The initial values are ( ) ( )
Fig. (4.1).

4. 24
( ) ( ) ( )
Further, ( ) ( )
For bender -Schmidt formula gives
( )
( )
( )
Similarly for , we obtain
( )
( )
( )
(2). The crank- Nicholson method
We have seen that the Schmidt scheme is computationally simple and for
convergent results ⁄ To obtain more accurate
results, should be small i.e. is necessarily very small. This makes the
computations exceptionally lengthy as more time-levels would be
required to cover the region. A method that does not restrict and also
reduces the volume of calculation was proposed by Crank and Nicolson
in 1947. According to this methods, ⁄ is replaced by the average
of its central-difference approximations on the and ( ) time
rows. Thus (4.1) is reduced to.

5. 25
{ }
{ }
Or ( )
( ) ( )
Where ⁄
Clearly the left side of (4.4) contains three unknown values of u at the
( ) level while all the three values on the right are known values
at the level. Thus (4.4) is a 2-level implicit relation and is known as
Crank–Nicolson formula. It is convergent for all finite values of It is
computational model is given in Fig. (4.2).
( ) ( ) ( ) ( ) level
level
( ) ( ) (i+1, j)
The crank-Nicholson grid. Fig (4.2).
If there are n internal mesh points on each row, then the relation (4.4)
gives n simultaneous equations for the n unknown values in terms of the
unknown boundary values. These equations can be solved to obtain the

6. 26
i
values at these mesh points. Similarly, the values at the interval mesh
points at all rows can be found. A method such as this in which the
calculation, of a known mesh value necessitates the solution of a set of
simultaneous equation, is known as an implicit scheme.
Example: 2
Solve the equation by crank-Nicholson
method.
Given that ( ) ( ) ( )
Solution:
By Giving and , taking , we get .
j 0 1 2 3 4 5
0 0 20 20 20 20 100
1 0 100
Then crank-Nicolson formula becomes
= 0+20+0+ i.e ( )
= 20+20+ + i.e ( )
= 20+20+ + i.e ( )
= 20+100+ +100 i.e ( )
Now ( ) ( ) gives =180 ( )
4( ) ( ) give ( )
Then15( ) – 4( ) gives 209 ie
Table (4.1)

7. 27
From( ) we get i.e = 30.75
From ( ) we get i.e = 10.05
From ( ) we get
i.e = 62.69
Thus the required values are 10.05, 20.2, 30.75 and 62.68.
(3). Iterative method for an explicit scheme
The iterative methods can be applied to solve the finite-difference
equations can be obtained in the preceding section. In the Crank-Nicolson
method we have
( ) ( )
(4.4)
A B C
0
D E F
( ) [ ] ( )
= [ ]
Fig(4.3).

8. 28
[ ] [ ]
[ ] [ ]
Or an Implicit scheme from (3.4) we have
(1+ ) = ( + ) + + ( 2 + )
(4.5)
Here only , and are unknown while all others are
known since these were already computed in the th step
Denote: = + ( + ) (4.6)
And dropping (4.6) becomes =
( )
( + ) +
This gives the iteration formula
=
( )
{ ( ) ( )
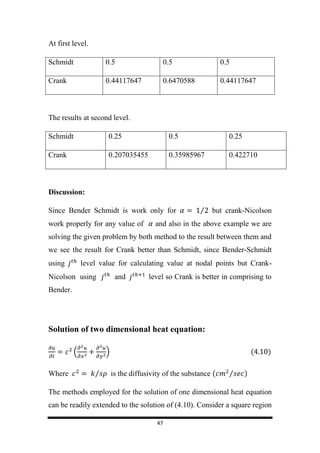
} + (4.7)
Which expresses the ( ) iterates in terms of the iterates only.
This is known as the Jacobi iteration formula,
As the latest value of i.e. ( )
is already available the
convergence of the iteration formula (4.7) can be improved by replacing
by A accordingly (4.7) may be written as
=
( )
{ ( ) ( )
} + (4.8)
This is known as Gauss-Seidal iteration formula

9. 29
Remark. Gauss-Seidal iteration scheme is valid for all finite value of
and converges twice as fast as Jacobi’s scheme.
Example: 3
Solve Subject to the initial condition,
and u = 0 at x = 0 and x = 1 for
, by Gauss-Seidel method.
Solution:
We choose = ⁄ ⁄
when we use their value in equation (4.8), it gives the equation
( )
[
( ) ( )
] Let the values of u at the interior
mesh points on the row corresponding to t = 0.02 as shown
in fig (4.4). Now when we apply the above formula given at the four
interior mesh points, the following results are obtained,
when
( )
[
( )
] ( )
( )
[
( )
] ( )
( )
[
( ) ( )
] (
) ( )
= [
( ) ( )
]
( )
[
( ) ( )
] (
) ( )

10. 30
( )
[
( )
] ( )
= [
( )
] ( )
0.02
0 0.2 0.4 0.6 0.8 1.0
0.0 0.5878 0.9511 0.5878 0.9511 0.0
We can now use equations ( i, ii, iii, iv, ) to obtain better approximations
For respectively. The table (4.2) below gives the
Successive iterates of corresponding to .
Fig. (4.4).

11. 31
(4). Du fort and Frankel method:
If we replace the derivatives in (4.1) by the central difference
approximations,
and
We obtain = [ ]
i.e. = +2 [ ] (4.8)
Where ⁄ this difference equation is called the Richardson
Scheme which is a 3-level method.
0.0 0.2 0.4 0.6 0.8 1.0
u=(x) 0.0 0.5878 0.9511 0.9511 0.5878 0.0
n=0 0.0 0.5878 0.9511 0.9511 0.5878 0.0
n=1 0.0 0.5129 0.8176 0.8078 0.4890 0.0
n=2 0.0 0.4907 0.7900 0.7868 0.4855 0.0
n=3 0.0 o.4861 0.7858 0.7855 0.4853 0.0
n=4 0.0 0.4854 0.7854 0.7854 0.4853 0.0
n=5 0.0 0.4853 0.7854 0.7854 0.4853 0.0

12. 32
If we replace by the mean of the value and i.e
( + ) in (4.8), then we get
= [ + 2 ( + ) + ]
On simplification it can be written as
= + { } (4.9)
This difference scheme is called Du fort Frankel method which is a
3-level explicit method. Its computational model is given in fig (4.5).
( ) ( )th level
( ) ( ) j th level
( ) ( ) th level
Example: 4
Solve the equation
Fig (4.5).

13. 33
Subject to the conditions ( ) ( )
( ) using the Du fort–Frankel method, carry out. Computations
for two levels, taking
Solution:
Here
Also the initial values are √ √
and all boundary values are zero.
By Du fort-Frankel formula
[ ]
To start the calculations we need
We may take from Schmidt method
For :
[ ] [√ ⁄ ]
[ ] [√ ⁄ ]
Comparative study of different methods
We are solving heat equation by finite difference method and comparing
both results which are obtained by Bender-Schmidt and Crank Nicolson
Methods with analytical solution.

14. 34
Example: 5
Find the analytical solution of the parabolic equation when
( ) ( ) and ( ) ( ) taking , and ,
Find the values up to .
Solution:
It is already given parabolic equation
and also given the boundary condition, ( ) ( )
the initial condition ( ) ( ) we can write parabolic equation
in the form,
(1)
where
Let (2)
where is the function of only and is the function of only.
Differentiating (2) partially , we get
(3)
(4)
Let (3) and (4) equal
Put the values of ( ) and ( ) in (1) we get,

15. 35
= =
Separating variables, we get
Where
Now,
We have, , put the value of and in equation (2) we get,
( ) (5)

16. 36
Now, put the value of ( ) , where in equation (5), we get
Let arbitrary constant we have so
( ) (6)
put the value of ( ) , where in equation (6), we get
Put the value of p in equation (6)
( )
( )
( )
( )
(7)
Where ∑
∑ ( )
( )
(8)
Now we find the value of by Fourier series,
∫ ( ) ( )
∫ ( ) ( )

17. 37
∫ ( ) ∫ ( ) (9)
Integration first part from equation (9) by the form of integral,
+……
[
( )
( )
( )
( )
]
( )
(10)
Integration second part from equation (9)
[{
( )
( )
} {
( )
( )
} {
( )
( )
} ]
[
( )
{
( )
}]
[
( )
( )]
[ ( )] (11)
putting the value of (10) and (11) in (9) we get,
( )
4
4
0
0
4
[

18. 38
( )
When = 0
( )
Put value of in equation (8), we get
( )
( )
(12)
Where
√
( )
√
( )
( )
( )
.
Analytical solution for
Now we solve (Example: 5) by numerical methods

19. 39
Find the solution of the parabolic equation when ( )
( ) and ( ) ( ) taking . Find the values up to
.
Solution:
Given a parabolic equation
Also given the boundary condition, ( ) ( )
and the initial condition ( ) ( )
when we put the value of in the relation of the initial
condition, it gives that,
( ) ( ) ( ) ( ) ( )
we have , using these values we can find
By Schmidt method must be
By Schmidt formula the following results are obtained,
[ ]
When and

20. 40
When
When
Now solve by Crank-Nicolson formula:
( )
( )
Put
When
( )
( )
( )

21. 41
When the initial conditions are given in ( ) ( ) ( ) we get.
( )
( )
( )
When we solve the equations ( ) ( ) ( ) by manual or by calculator it
gives that,
,
When
In the same way can we find
,
Result: First step using the Analytical solution and Crank-Nicolson,
Bender-Schmidt,
Analytical result 2.1356 3.032585 2.1356
Schmidt 2 3 2
Crank 2.176470588 3.0588233529 2.176470588
Second step using the Crank-Nicolson and Bender-Schmidt
Schmidt 1.5 2 1.5
Crank 1.615916955 2.283737023 1.615916955

22. 42
Discussion:
The results obtained by analytical methods are always providing accurate
solution but numerical solution always providing approximate result. But
among these numerical methods Crank-Nicolson method was providing
fast convergence in comparison to Bender-Schmidt method. Since it is
not possible to solve every partial differential equation analytically so
numerical methods providing a good agreement in those cases where
solutions not exist or we are unable to solve partial differential equation
analytically.
Example: 6
Solve the heat equation subject to the condition
( ) ( )
⁄
( )
( ) ⁄
Take and according to Bandre-Schmidt equation.
Solution:
Using Bandre-Schmidt formula
from Bandre-Schmidt equation. and
now we find

23. 43
Initial condition when ⁄
( )
( )
Initial condition when
( )
( )
( )
By using Bandre-Schmidt method.
When
[ ]

24. 44
When
When
Boundary t boundary condition
0 u12 u13 u14 0
0 u7 u8 u9 0
0 u2 u3 u4 0
0 12 1 1 0
0 14 12 34 1 x
Fig (4.8)

25. 45
Table of the value:
j i 0 1 2 3 4
0 0 0.5 1 0.5 0
1 0 0.5 0.5 0.5 0
2 0 0.25 0.25 0.25 0
3 0 0.25 0.25 0.25 0
Fig (4.9)
Now, solve by crank-Nicolson method:
Crank-Formula is given below,
( ) (
)
When and the formula will be
The initial conditions are ( ) , ( ) ( ) ,
( ) ( )
When

26. 46
3
When we solve the equations we get,
When
When solving these equations we get,
,
Now, the results which are obtained by Bender-Schmidt and Crank
Nicolson methods are given below,
The results obtained by Crank-Nicolson and Schmidt methods are given
in the following table.

27. 47
At first level.
Schmidt 0.5 0.5 0.5
Crank 0.44117647 0.6470588 0.44117647
The results at second level.
Schmidt 0.25 0.5 0.25
Crank 0.207035455 0.35985967 0.422710
Discussion:
Since Bender Schmidt is work only for ⁄ but crank-Nicolson
work properly for any value of and also in the above example we are
solving the given problem by both method to the result between them and
we see the result for Crank better than Schmidt, since Bender-Schmidt
using level value for calculating value at nodal points but Crank-
Nicolson using and level so Crank is better in comprising to
Bender.
Solution of two dimensional heat equation:
( ) ( )
Where ⁄ is the diffusivity of the substance ( ⁄ )
The methods employed for the solution of one dimensional heat equation
can be readily extended to the solution of (4.10). Consider a square region

28. 48
and assume that u is known at all points within and
the boundary of this square
fig. (4.6)
If be the step–size then a mesh point ( ) ( ) may
be denoted as simply( ). By replacing the derivatives in (4.10) by
their finite difference approximation, we get,

29. 49
{( ) (
)}
( )
( )
Where ⁄
This equation needs the five points available on the nth plane.
The computation process consists of point-by point evaluation in the
( ) the plane using the points on the nth plane. It is followed by
plane-By–plane evaluation. This method is known as ADE (Alternating
Direction Explicit) method.
Example: 7
Solve the equation subject to the initial conditions
( ) and the conditions
( ) on the boundaries, using ADE method with
(calculate the results for one time level).
Solution:
From the equation (4.11) for two dimensions becomes,
( )
( ) ( )
The mesh points and the computational model is given in fig (4.7).
At the zeros level ( ) the initial and boundary condition a

30. 50
fig (4.7).

31. 51
and
Now we calculate the mesh values at the first level:
For ( ) gives
( ) ( )
( ) ( ) we get
( )
( ) + ( )
(
√ √ √ √
)
( ) in (2)
( )
{( ) ( ) }
(
√
) { (
√
) (
√
) }
( ) in (2)
( )

32. 52
{ ( ) ( ) }
( )
( ) in (2)
( )
( ) ( )
( )
Similarly the mesh values at the second and higher level can be
calculated.