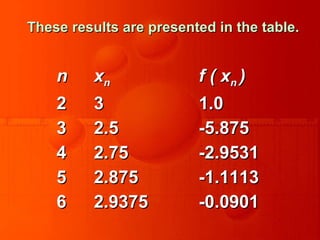
This document discusses various numerical methods for solving non-linear equations, emphasizing techniques such as the bisection method, regula-falsi method, Newton-Raphson method, and others. It explains the classification of equations into algebraic and transcendental, describes properties and roots of algebraic equations, and outlines the conditions for the existence of roots. The document also highlights graphical and analytical methods for obtaining initial approximations of roots.

1. Lecture 3
Numerical
Analysis

2. Solution of
Non-Linear
Equations
Chapter 2

3. Introduction
Bisection Method
Regula-Falsi Method
Method of iteration
Newton - Raphson Method
Muller’s Method
Graeffe’s Root Squaring
Method

4. Definition: The equationDefinition: The equation
f (x) = 0 is called anf (x) = 0 is called an
algebraic, if it is purely aalgebraic, if it is purely a
polynomial in x;polynomial in x;
it is a transcendental if f (x)it is a transcendental if f (x)
contains trigonometric,contains trigonometric,
exponential or logarithmicexponential or logarithmic
functionsfunctions

5. For example,For example,
is an algebraic equation,is an algebraic equation,
WhereasWhereas
andand
are transcendental equations.are transcendental equations.
3 2
5 6 3 0x x x+ − + =
sinM E e E= −
2
log( 3) sin 0x
ax x e x+ − + =

6. To find the solution of anTo find the solution of an
equationequation ff ((xx) = 0, we find) = 0, we find
those values ofthose values of xx for whichfor which
ff ((xx) = 0 is satisfied.) = 0 is satisfied.
Such values ofSuch values of xx are calledare called
the roots ofthe roots of ff ((xx) = 0.) = 0.
Thus a is a root of anThus a is a root of an
equationequation ff ((xx) = 0, if and only) = 0, if and only
if,if, ff ((aa) = 0.) = 0.

7. Properties of anProperties of an
algebraic equationalgebraic equation
Every algebraic equationEvery algebraic equation
ofof n-thn-th degree, wheredegree, where nn
is a positive integer, hasis a positive integer, has
nn and onlyand only nn roots.roots.

8. Complex roots occur in pairs.Complex roots occur in pairs.
That is, if (That is, if (a + iba + ib) is a root of) is a root of
ff ((xx) = 0, then () = 0, then (a – iba – ib) is also a) is also a
root of this equation.root of this equation.
IfIf x = ax = a is a root ofis a root of ff ((xx) = 0, a) = 0, a
polynomial of degreepolynomial of degree nn, then, then
((x – ax – a) is a factor of) is a factor of ff ((xx). On). On
dividingdividing ff ((xx) by () by (x – ax – a) we obtain) we obtain
a polynomial of degree (a polynomial of degree (nn – 1).– 1).

9. Descartes rule of signs:Descartes rule of signs:
The number of positive roots of anThe number of positive roots of an
algebraic equationalgebraic equation ff ((xx) = 0 with real) = 0 with real
coefficients cannot exceed thecoefficients cannot exceed the
number of changes in sign of thenumber of changes in sign of the
coefficients in the polynomialcoefficients in the polynomial ff ((xx) = 0.) = 0.
Similarly, the number of negative rootsSimilarly, the number of negative roots
ofof ff ((xx) = 0 cannot exceed the number) = 0 cannot exceed the number
of changes in the sign of theof changes in the sign of the
coefficients ofcoefficients of ff ((-x-x) = 0.) = 0.

10. For example, consider anFor example, consider an
equationequation
As there are three changes inAs there are three changes in
sign, so, the degree of thesign, so, the degree of the
equation is three, and hence theequation is three, and hence the
given equation will have all thegiven equation will have all the
three positive roots.three positive roots.
3 2
3 4 5 0x x x− + − =

11. Intermediate value property:Intermediate value property:
IfIf ff ((xx) is a real valued continuous) is a real valued continuous
function in the closed intervalfunction in the closed interval
IfIf ff ((aa) and) and ff ((bb) have opposite) have opposite
once; that isonce; that is ff ((xx) = 0 has at least) = 0 has at least
one root such thatone root such that
a x b≤ ≤
β
a bβ< <

12. Numerical methods for solvingNumerical methods for solving
either a transcendental equation oreither a transcendental equation or
an algebraic equation are classifiedan algebraic equation are classified
into two groups:into two groups:
Direct methodsDirect methods, which require no, which require no
knowledge of the initialknowledge of the initial
approximation of a root of theapproximation of a root of the
equationequation ff ((xx) = 0.) = 0.
Iterative methodsIterative methods, require first, require first
approximation to initiate iteration.approximation to initiate iteration.

13. How to get the firstHow to get the first
approximation?approximation?
We can find the approximateWe can find the approximate
value of the root ofvalue of the root of ff ((xx) = 0) = 0
either byeither by graphical methodgraphical method
or by anor by an analytical methodanalytical method

14. Graphical methodGraphical method
The equationThe equation ff ((xx) = 0 can be) = 0 can be
rewritten asrewritten as ff11((xx) =) = ff22((xx) and the first) and the first
approximation to a root ofapproximation to a root of ff ((xx) = 0) = 0
can be taken as the abscissa of thecan be taken as the abscissa of the
point of intersection of the graphspoint of intersection of the graphs
ofof yy == ff11((xx) and) and yy == ff22((xx).).
For example, consider,For example, consider,
( ) sin 1 0f x x x= − − =

15. It can be written asIt can be written as xx – 1 =– 1 = sin xsin x..
Now, we shall draw the graphsNow, we shall draw the graphs
ofof yy =(=(xx -1) and-1) and y = sin xy = sin x

16. Answer !Answer !
The approximateThe approximate
value of the rootvalue of the root
is found to be 1.9is found to be 1.9

17. Analytical methodAnalytical method
This method is based onThis method is based on
‘intermediate value property’.‘intermediate value property’.
( ) 3 1 sin 0f x x x= − + =
(0) 1
180
(1) 3 1 sin 1 3 1 0.84147 1.64299
f
f
π
= −
 
= − + × = − + = ÷
 

18. HereHere ff (0) and(0) and ff (1) are of(1) are of
opposite signs. Therefore, usingopposite signs. Therefore, using
intermediate value property weintermediate value property we
infer that there is at least oneinfer that there is at least one
root betweenroot between xx = 0 and= 0 and xx = 1.= 1.
This method is often used toThis method is often used to
find the first approximation to afind the first approximation to a
root of either transcendentalroot of either transcendental
equation or algebraic equation.equation or algebraic equation.

19. Hence, in analyticalHence, in analytical
method, we mustmethod, we must
always start with analways start with an
initial interval (initial interval (a, ba, b),),
so thatso that ff ((aa) and) and ff ((bb))
have opposite signs.have opposite signs.

20. Bisection
Method
(Bolzano)

21. Suppose, we wish to locate theSuppose, we wish to locate the
root of an equationroot of an equation ff ((xx) = 0 in an) = 0 in an
interval, say (interval, say (xx00,, xx11). Let). Let ff ((xx00) and) and ff
((xx11) are of opposite signs, such) are of opposite signs, such
thatthat ff ((xx00)) ff ((xx11) < 0.) < 0.
Then the graph of the functionThen the graph of the function
crosses thecrosses the xx-axis between-axis between xx00 andand
xx11, which guarantees the existence, which guarantees the existence
of at least one root in the intervalof at least one root in the interval
((xx00,, xx11).).

22. The desired root isThe desired root is
approximately defined by theapproximately defined by the
midpointmidpoint
IfIf ff ((xx22) = 0, then) = 0, then xx22 is theis the
desired root ofdesired root of ff ((xx) = 0.) = 0.
However, ifHowever, if f (xf (x22) 0) 0 then thethen the
root may be betweenroot may be between xx00 andand xx22
oror xx22 andand xx11..
0 1
2
2
x x
x
+
=
≠

23. Now, we define the nextNow, we define the next
approximation byapproximation by
providedprovided ff ((xx00)) ff ((xx22) < 0, then the) < 0, then the
root may be found betweenroot may be found between xx00 andand
xx22 or byor by
providedprovided ff ((xx11)) ff ((xx22) < 0, then the) < 0, then the
root lies betweenroot lies between xx11 andand xx22 etc.etc.
0 2
3
2
x x
x
+
=
1 2
3
2
x x
x
+
=

24. Thus, at each step, we either find theThus, at each step, we either find the
desired root to the requireddesired root to the required
accuracy or narrow the range to halfaccuracy or narrow the range to half
the previous interval.the previous interval.
This process of halving the intervalsThis process of halving the intervals
is continued to determine a smalleris continued to determine a smaller
and smaller interval within which theand smaller interval within which the
desired root lies.desired root lies.
Continuation of this processContinuation of this process
eventually gives us the desired root.eventually gives us the desired root.

25. ExampleExample
SolveSolve xx33
– 9– 9xx + 1 = 0+ 1 = 0
for the root betweenfor the root between
xx = 2 and= 2 and xx = 4 by the= 4 by the
bisection method.bisection method.

26. Solution GivenSolution Given ff ((xx) =) = xx33
– 9– 9xx + 1.+ 1.
HereHere ff (2) = -9,(2) = -9, ff (4) = 29.(4) = 29.
Therefore,Therefore, ff (2)(2) ff (4) < 0 and hence(4) < 0 and hence
the root lies between 2 and 4.the root lies between 2 and 4.
LetLet xx00 = 2,= 2, xx11 = 4. Now, we define= 4. Now, we define
as a first approximation to a root ofas a first approximation to a root of
ff ((xx) = 0 and note that) = 0 and note that ff (3) = 1, so(3) = 1, so
thatthat ff (2)(2) ff (3) < 0.(3) < 0. Thus the root liesThus the root lies
between 2 and 3between 2 and 3
0 1
2
2 4
3
2 2
x x
x
+ +
= = =

27. We further define,We further define,
and note thatand note that ff ((xx33) =) = ff (2.5) < 0, so that(2.5) < 0, so that ff
(2.5)(2.5) ff (3) < 0. Therefore, we define the(3) < 0. Therefore, we define the
mid-point,mid-point,
Similarly,Similarly, xx55 = 2 . 875 and= 2 . 875 and xx66 = 2.9375= 2.9375
and the process can be continued untiland the process can be continued until
the root is obtained to the desiredthe root is obtained to the desired
accuracy.accuracy.
0 2
3
2 3
2.5
2 2
x x
x
+ +
= = =
3 2
4
2.5 3
2.75, etc.
2 2
x x
x
+ +
= = =

28. These results are presented in the table.These results are presented in the table.
nn xxnn f ( xf ( xnn ))
22 33 1.01.0
33 2.52.5 -5.875-5.875
44 2.752.75 -2.9531-2.9531
55 2.8752.875 -1.1113-1.1113
66 2.93752.9375 -0.0901-0.0901

29. Lecture 3
Numerical
Analysis