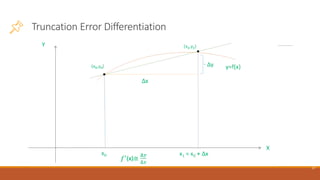
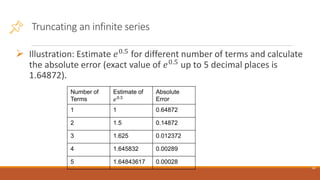
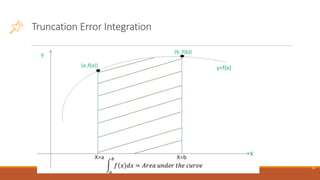
This document discusses numerical methods and sources of error in numerical analysis. It defines numerical analysis as using approximate solutions to solve complex mathematical problems. Numerical methods break problems into steps to find solutions. Errors can occur from modeling assumptions or approximations in calculations. Round-off error results from representing numbers approximately. Truncation error occurs when infinite processes are truncated to a finite number of steps, such as limiting infinite series or integrals to a certain number of terms. The document shows that truncation error decreases with smaller step sizes or more terms in approximations.

1. Numerical Methods:
Introduction, Accuracy, Errors
ADVANCED ENGINEERING MATHEMATICS: LESSON 5
PREPARED BY: ENGR. APRIL JOY F. AGUADO
COLLEGE OF ENGINEERING AND ARCHITECTURE

2. What is a Numerical Analysis?
➢ Numerical Analysis is a branch of
mathematics which deals with the
approximate solutions of
mathematical problems.
2

3. What are numerical methods?
➢ Are methods of obtaining solution by subjecting the
original problem to a series of steps or repetitions.
➢ Numerical Methods develop accurate and fast
approximations to problems whose exact solutions
are difficult to find because of their complexity.
3

4. Common Ways to Express Error
1. Absolute Error (AE) = 𝑥 − 𝑥′
where 𝑥′ = is the approximate value
𝑥 = is the exact value
2. Relative Error (RE) =
𝑥−𝑥′
𝑥
=
𝐴𝐸
𝑇𝑟𝑢𝑒 𝑉𝑎𝑙𝑢𝑒
3. Percentage Error = RE x 100
4

5. Accuracy vs Precision
➢ Accuracy – is the closeness of values to its true
value.
➢ Precision – is the closeness of values to each
other.
5

6. Sources of Error
➢ Modeling Error
o Blunders
o Formulation Error
o Data Uncertainty
➢ Numerical Error
o Round-off Error
o Truncation Error
6

7. Round-off Error
➢ Round-off error – error created due to
approximate representation of numbers
7

8. Truncation Error
➢ Truncation Error – is an error due to truncating a process involving
infinite number of steps to finite number of steps
➢ Error due to numerical approximation method
o Limiting infinite series to finite number of terms
o Limiting infinite number of iterations for finite number of
iterations
o Taking finite step size instead of infinitesimal step size (numerical
differentiation and numerical integration)
8

9. Truncating an infinite series
➢ Maclaurin series of 𝑒𝑥 = 1 +
𝑥
1
+
𝑥2
2!
+
𝑥3
3!
+
𝑥4
4!
+ ⋯
➢ Use the terms on the right side to determine the value of 𝑒𝑥
➢ We cannot use infinite terms: say we use only first four terms
➢ Approximate 𝑒𝑥
by 𝑒𝑥
≈ 1 +
𝑥
1
+
𝑥2
2!
+
𝑥3
3!
➢ Truncation Error = 𝑒𝑥
−
𝑥
1
+
𝑥2
2!
+
𝑥3
3!
=
𝑥4
4!
+
𝑥5
5!
+ ⋯
9

10. Truncating an infinite series
➢ Illustration: Estimate 𝑒0.5
for different number of terms and calculate
the absolute error (exact value of 𝑒0.5 up to 5 decimal places is
1.64872).
10
Number of
Terms
Estimate of
𝑒0.5
Absolute
Error
1 1 0.64872
2 1.5 0.14872
3 1.625 0.012372
4 1.645832 0.00289
5 1.64843617 0.00028

11. Truncation Error Integration
11

12. Truncation Error in Integration
➢ ‫׬‬2
4
𝑥2
𝑑𝑥 =
𝑥3
3
in 2 to 4 =
43−23
3
=
64−8
3
= 18.67 gives exact value
rounded to 2 decimal places
➢ Let us apply numerical approximation method:
o For simplicity, ease and convenience and to avoid round-off errors,
take rectangles of width 1 from 2 to 4 and sum up their areas as an
estimate of the integral ‫׬‬2
4
𝑥2 𝑑𝑥 giving us
o Estimate value 𝐼a = 1 4 + 1 9 = 13 (Height 22 and 42)
o Truncation Error = 18.67-13=5.67
12

13. Truncation Error Integration
13

14. Truncation Error in Integration
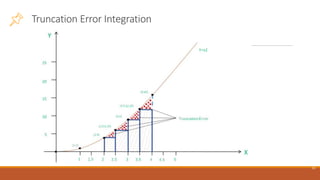
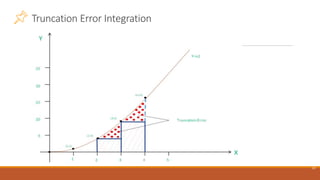
➢ What would happen, if we rework the same example with smaller
width? (smaller size and increase the number of steps)
➢ Let number of subintervals now in [2,4] be 4 instead of just 2
➢ Width of each rectangle would be now 0.5
➢ Heights would be 4, 6.25, 9, 12.5
➢ 𝐼𝑎 = 0.5 4 + 6.25 + 9 + 12.25 = 15.75
➢ Truncation error = 18.67-15.75=2.92 (reduction from 5.67 to 2.92)
14

15. Truncation Error Integration
15

16. Truncation Error in Differentiation
➢ Take 𝑓 𝑥 = 𝑥3
and let us estimate derivative at 𝑥 = 2
➢ 𝑓′
𝑥 = 3𝑥2
; 𝑓′
2 = 3 22
= 12 (true value)
➢ The derivative is defines as 𝑓′
𝑥 = lim
ℎ→0
𝑓 𝑥+ℎ −𝑓(𝑥)
ℎ
➢ Let us estimate derivative of 2 by taking ℎ = 0.1
➢ 𝑓′
2 ≅
𝑓 2.1 −𝑓 2
0.1
=
2.13−23
0.1
= 12.61 giving an absolute error of 0.61
16

17. Truncation Error Differentiation
17

18. Truncation Error in Differentiation
➢ If we reduce ℎ to 0.05 and repeat the same exercise, estimate
obtained is
➢ 𝑓′
2 ≅
𝑓 2.05 −𝑓 2
0.05
=
2.053−23
0.1
= 12.3025 giving an absolute error of
0.3025
18

19. Observation
➢ Truncation error
o Arises due to numerical approximation method being applied to
solve the problem
o Arises basically due to truncating the process to finite number of
steps
o As step size is reduce, truncation error decreases
o Reduction in step size ↔ increase in number of steps
19

20. 20
ALL is WELL. TRUST the PROCESS.
KEEP FIGHTING, FUTURE ENGINEERS!
-
Ma’am A