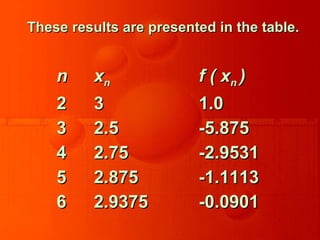
The document discusses numerical methods for solving non-linear equations, focusing on the bisection method and the regula-falsi method. It provides detailed examples of how to find roots of specific equations using these methods, including step-by-step approximations and the significance of choosing appropriate intervals for initial guesses. Key observations highlight differences in approximations and emphasize the need for sufficiently small intervals to improve accuracy.

1. Lecture 4
Numerical
Analysis

2. Solution of
Non-Linear
Equations
Chapter 2

3. Introduction
Bisection Method
Regula-Falsi Method
Method of iteration
Newton - Raphson Method
Muller’s Method
Graeffe’s Root Squaring
Method

4. Bisection
Method
(Bolzano)

5. ExampleExample
SolveSolve xx33
– 9– 9xx + 1 = 0+ 1 = 0
for the root betweenfor the root between
xx = 2 and= 2 and xx = 4 by the= 4 by the
bisection method.bisection method.

6. Solution GivenSolution Given ff ((xx) =) = xx33
– 9– 9xx + 1.+ 1.
HereHere ff (2) = -9,(2) = -9, ff (4) = 29.(4) = 29.
Therefore,Therefore, ff (2)(2) ff (4) < 0 and hence(4) < 0 and hence
the root lies between 2 and 4.the root lies between 2 and 4.
LetLet xx00 = 2,= 2, xx11 = 4. Now, we define= 4. Now, we define
as a first approximation to a root ofas a first approximation to a root of
ff ((xx) = 0 and note that) = 0 and note that ff (3) = 1, so(3) = 1, so
thatthat ff (2)(2) ff (3) < 0.(3) < 0. Thus the root liesThus the root lies
between 2 and 3between 2 and 3
0 1
2
2 4
3
2 2
x x
x
+ +
= = =

7. We further define,We further define,
and note thatand note that ff ((xx33) =) = ff (2.5) < 0, so that(2.5) < 0, so that
ff (2.5)(2.5) ff (3) < 0. Therefore, we define the(3) < 0. Therefore, we define the
mid-point,mid-point,
Similarly,Similarly, xx55 = 2 . 875 and= 2 . 875 and xx66 = 2.9375= 2.9375
and the process can be continued untiland the process can be continued until
the root is obtained to the desiredthe root is obtained to the desired
accuracy.accuracy.
0 2
3
2 3
2.5
2 2
x x
x
+ +
= = =
3 2
4
2.5 3
2.75, etc.
2 2
x x
x
+ +
= = =

8. These results are presented in the table.These results are presented in the table.
nn xxnn f ( xf ( xnn ))
22 33 1.01.0
33 2.52.5 -5.875-5.875
44 2.752.75 -2.9531-2.9531
55 2.8752.875 -1.1113-1.1113
66 2.93752.9375 -0.0901-0.0901

9. Regula-Falsi
Method
Method of falseMethod of false
positionposition
Method of falseMethod of false
positionposition

10. Here, we choose two points xn
and xn -1 such that f (xn) and f
(xn-1) are of opposite signs.
Intermediate value property
suggests that the graph of
y = f (x) crosses the x-axis
between these two points and
therefore, a root say lies
between these two points.

11. Thus, to find a real root of
f (x) = 0 using Regula-Falsi
method, we replace the part of
the curve between the points
A[xn, f(xn)] and B[xn-1, f (xn-1)] by
a chord in that interval and we
take the point of intersection of
this chord with the x-axis as a
first approximation to the root.

12. Now, the equation of the chord
joining the points A and B is
(2.1)
Setting y = 0 in Eq. (2.1), we get
1 1
( )
( ) ( )
n n
n nn n
y f x x x
f x f x x x− −
− −
=
− −
1
1
( )
( ) ( )
n n
n n
n n
x x
x x f x
f x f x
−
−
−
= −
−

13. Hence, the first approximation to the root
of f (x) = 0 is given by
(2.2)
we observe that f (xn-1) and f (xn+1) are of
opposite sign. Thus, it is possible to
apply to above procedure, to determine
the line through B and A1 and so on.
Hence, the successive approximations to
the root of f (x) = 0 is given by Eq. (2.2).
1
1
1
( )
( ) ( )
n n
n n n
n n
x x
x x f x
f x f x
−
+
−
−
= −
−

14. Example
Use the Regula-Falsi method to
compute a real root of the equation
x3
– 9x + 1 = 0,
(i) if the root lies between 2 and 4
(ii) if the root lies between 2 and 3.
Comment on the results.

15. Solution
Let f (x) = x3
– 9x + 1.
f (2) = – 9 and f (4) = 29.
Since f (2) and f (4) are of
opposite signs, the root of
f (x) = 0 lies between 2 and 4.

16. Taking x1 = 2, x2 = 4 and
using Regula-Falsi method,
the first approximation is
given by
2 1
3 2 2
2 1
( )
( ) ( )
2 29
4 2.47368
38
x x
x x f x
f x f x
−
= −
−
×
= − =

17. Now f (x3) = –6.12644.
Since f (x2) and f (x3) are of
opposite signs, the root lies
between x2 and x3.
The second approximation to the
root is given as
3 2
4 3 3
3 2
( )
( ) ( )
2.73989
x x
x x f x
f x f x
−
= −
−
=

18. Therefore f (x4) = – 3. 090707.
Now, since f (x2) and f (x4) are
of opposite signs, the third
approximation is obtained
from
and f (x5) = – 1.32686.
4 2
5 4 4
4 2
( ) 2.86125
( ) ( )
x x
x x f x
f x f x
−
= − =
−

19. This procedure can be continued till
we get the desired result. The first
three iterations are shown as in the
table.
n xn+1 f (xn+1)
2 2.47368 -6.12644
3 2.73989 -3.090707
4 2.86125 -1.32686

20. (ii) f (2) = – 9 and f (3) = 1. Since
f (2) and f (3) are of opposite signs,
the root of f (x) = 0 lies between 2
and 3. Taking x1 = 2, x2 = 3 and
using Regula-Falsi method, the
first approximation is given by
3
2 1
3 2 2
2 1
( )
( ) ( )
1
3 2.9
10
( ) 0.711
x x
x x f x
f x f x
f x
−
= −
−
= − =
=−

21. Since f (x2) and f (x3) are of
opposite signs, the root lies
between x2 and x3.
The second approximation
to the root is given as
3 2
4 3 3
3 2
4
( ) 2.94156
( ) ( )
( ) 0.0207
x x
x x f x
f x f x
f x
−
= − =
−
= −

22. Now, we observe that f (x2)
and f (x4) are of opposite
signs, the third approximation
is obtained from
4 2
5 4 4
4 2
( )
( ) ( )
2.94275
( ) 0.0011896
x x
x x f x
f x f x
f x
−
= −
−
=
=−

23. This procedure can be
continued till we get the desired
result. The first three iterations
are shown as in the table.
n xn+1 f (xn+1)
2 2.9 -0.711
3 2.94156 -0.0207
4 2.94275 -0.0011896

24. We observe that the value of the
root as a third approximation is
evidently different in both the
cases, while the value of x5, when
the interval considered is (2,
3), is closer to the root.
Important observation: The initial
interval (x1, x2) in which the root of
the equation lies should be
sufficiently small.

25. Example
Use Regula-Falsi method to
find a real root of the equation
log x – cos x = 0
accurate to four decimal places
after three successive
approximations.

26. Solution
Given f (x) = log x – cos x.
We observe that
f (1) = 0-0.5403,and
f (2)=0.69315+0.41615=1.1093
Since f (1) and f (2) are of
opposite signs, the root lies
between x1 = 1, x2 = 2.

27. The first approximation is obtained
from
2 1
3 2 2
2 1
3
( )
( ) ( )
1.1093
2 1.3275
1.6496
( ) 02833 0.2409 0.0424
x x
x x f x
f x f x
f x
−
= −
−
= − =
= − =

28. Now, since f (x1) and f (x3) are
of opposite signs, the second
approximation is obtained as
4
3
4
(.3275)(.0424)
1.3275
0.0424 0.5403
1.3037
( ) 1.24816 10
x
f x −
= −
+
=
= ×

29. Similarly, we observe that f (x1)
and f (x4) are of opposite signs,
so, the third approximation is
given by
The required real root is 1.3030.
5
4
5
(0.3037)(0.001248)
1.3037
0.001248 0.5403
1.3030
( ) 0.6245 10
x
f x −
= −
+
=
= ×

30. Lecture 4
Numerical
Analysis