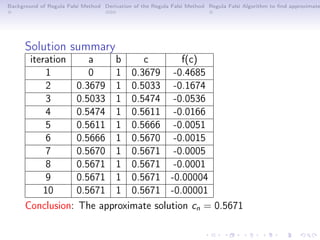
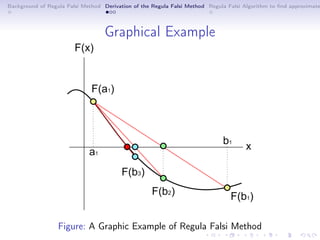
The document discusses the Regula Falsi (false position) method, a bracketing iterative technique for finding roots of nonlinear equations based on Bolzano's theorem. It includes the derivation and algorithm for the method, as well as a detailed example of finding a root for the function xex = 1 within the interval [0, 1]. The iterative process is summarized, demonstrating convergence to an approximate solution of 0.5671.

1. Regula Falsi (False Position) Method
Numerical Analysis
Isaac Amornortey Yowetu
NIMS-Ghana
September 12, 2020

2. Background of Regula Falsi Method Derivation of the Regula Falsi Method Regula Falsi Algorithm to find approximate
Application of Regula Falsi Method
Question
Find a root of xex
= 1 on I = [0, 1] using Regula Falsi method.

3. Background of Regula Falsi Method Derivation of the Regula Falsi Method Regula Falsi Algorithm to find approximate
Outline
Background of Regula Falsi Method
Derivation of the Regula Falsi Method
Graphical Example
Regula Falsi Algorithm to find approximate Solution
Application of Regula Falsi Method

4. Background of Regula Falsi Method Derivation of the Regula Falsi Method Regula Falsi Algorithm to find approximate
Background of Regula Falsi Method
Introduction
• It is one of the bracketing iterative methods in finding
roots of a nonlinear equations.
• The approximated root is found by the use of straight
lines or slopes.
• It is also noted to be based on Bolzano’s theorem for
continuous functions.
Theorem (Bolzano)
If a function f (x) is continuous on an interval [a, b] and
f (a) · f (b) < 0, then a value c ∈ (a, b) exists for which
f (c) = 0.

5. Background of Regula Falsi Method Derivation of the Regula Falsi Method Regula Falsi Algorithm to find approximate
Graphical Example
Figure: A Graphic Example of Regula Falsi Method

6. Background of Regula Falsi Method Derivation of the Regula Falsi Method Regula Falsi Algorithm to find approximate
Derivation of the Regula Falsi Method
∆y
∆x
=
f (a) − 0
a − c
=
f (b) − 0
b − c
(1)
OR
∆y
∆x
=
f (a) − f (b)
a − b
=
f (a) − 0
a − c
(2)
OR
∆y
∆x
=
f (a) − f (b)
a − b
=
f (b) − 0
b − c
(3)

7. Background of Regula Falsi Method Derivation of the Regula Falsi Method Regula Falsi Algorithm to find approximate
Derivation Continues...
Using any of the 3 approaches, can help us derived Regula
Falsi Method. Using eqn(1):
f (a) − 0
a − c
=
f (b) − 0
b − c
(4)
f (a)
a − c
=
f (b)
b − c
(5)
f (a)(b − c) = f (b)(a − c) (6)
b · f (a) − c · f (a) = a · f (b) − c · f (b) (7)
c · f (b) − c · f (a) = a · f (b) − b · f (a) (8)
c =
a · f (b) − b · f (a)
f (b) − f (a)
(9)

8. Background of Regula Falsi Method Derivation of the Regula Falsi Method Regula Falsi Algorithm to find approximate
Regula Falsi Algorithm
if f (a) · f (b) < 0:
root exists
else:
root doesn’t exist
Iteration Processes when root exists
1. Let c = a·f (b)−b·f (a)
f (b)−f (a)
2. If f (c) = 0, stop! c is the root.
3. if f (a) · f (c) < 0:
set b ← c
4. else if:
set a ← c
5. Go to the beginning and repeat till convergence.

9. Background of Regula Falsi Method Derivation of the Regula Falsi Method Regula Falsi Algorithm to find approximate
Application of Regula Falsi Method
Example 1
Find a root of xex
= 1 on I = [0, 1] using Regula Falsi method.
Solution
Considering our f (x) = xex
− 1 = 0 and a1 = 0, b1 = 1
f (0) = 0 · e0
− 1 = −1
f (1) = 1 · e1
− 1 = 1.7183
f (0) · f (1) < 0, hence c ∈ [0, 1].
c1 =
a · f (b) − b · f (a)
f (b) − f (a)
= 0.3679 (10)
f (c1) = −0.4685 (11)
choose [a2, b2] = [0.3679, 1]

10. Background of Regula Falsi Method Derivation of the Regula Falsi Method Regula Falsi Algorithm to find approximate
Solution Continue...
c2 =
a2 · f (b2) − b2 · f (a2)
f (b2) − f (a2)
= 0.5033 (12)
f (c2) = −0.1674 (13)
choose [a3, b3] = [0.5033, 1]
c3 =
a3 · f (b3) − b3 · f (a3)
f (b3) − f (a3)
= 0.5474 (14)
f (c3) = −0.0536 (15)
choose [a4, b4] = [0.5474, 1]

11. Background of Regula Falsi Method Derivation of the Regula Falsi Method Regula Falsi Algorithm to find approximate
Solution summary
iteration a b c f(c)
1 0 1 0.3679 -0.4685
2 0.3679 1 0.5033 -0.1674
3 0.5033 1 0.5474 -0.0536
4 0.5474 1 0.5611 -0.0166
5 0.5611 1 0.5666 -0.0051
6 0.5666 1 0.5670 -0.0015
7 0.5670 1 0.5671 -0.0005
8 0.5671 1 0.5671 -0.0001
9 0.5671 1 0.5671 -0.00004
10 0.5671 1 0.5671 -0.00001
Conclusion: The approximate solution cn = 0.5671

12. Background of Regula Falsi Method Derivation of the Regula Falsi Method Regula Falsi Algorithm to find approximate
End
THANK YOU