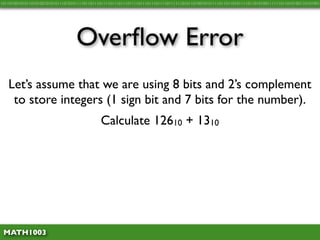
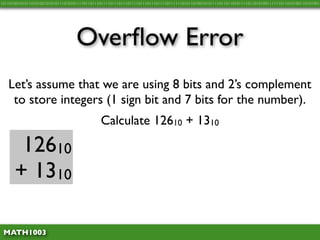
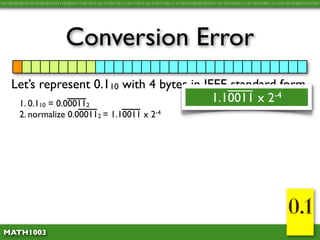
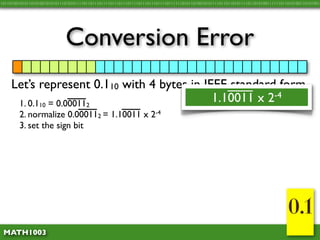
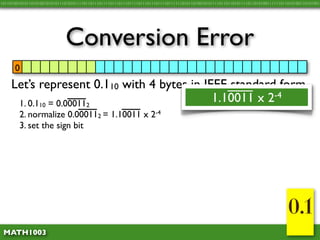
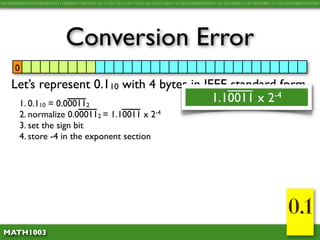
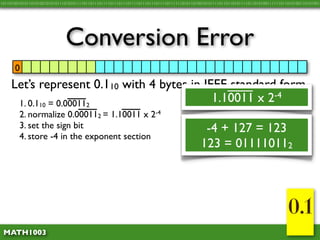
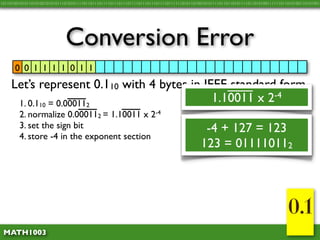
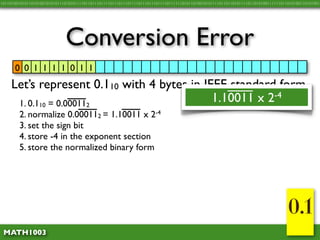
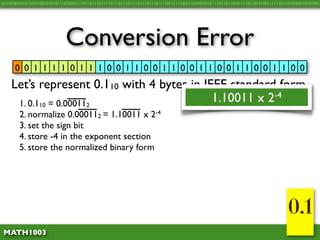
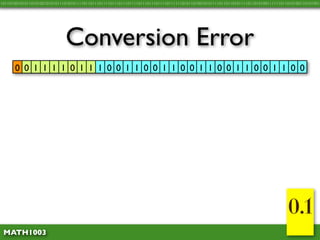
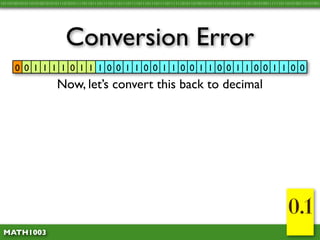
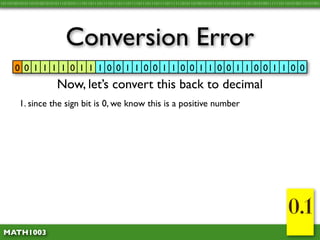
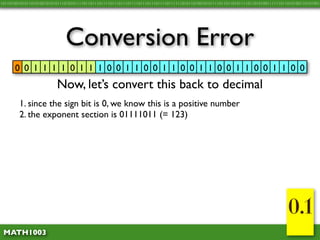
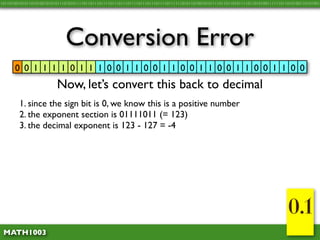
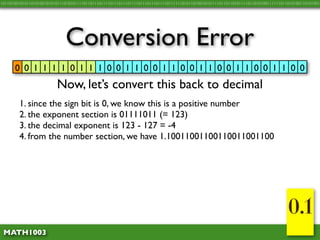
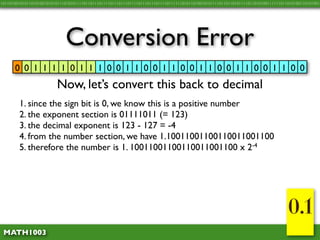
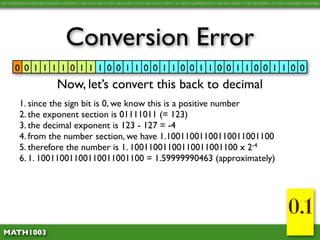
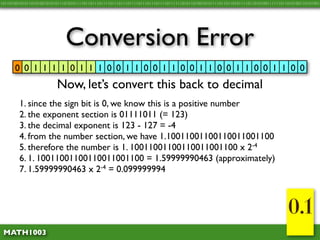
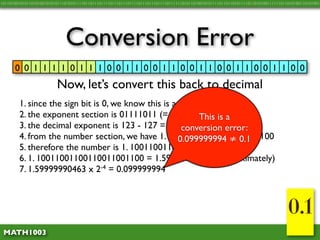
The document discusses several concepts related to errors that can occur when performing mathematical operations on a computer. It explains that computers have limited storage, so numbers are truncated or rounded. This can lead to truncation error when values are simply cut off. It also discusses overflow error, which occurs when a calculation produces a value that is too large for the computer's storage format. The goal is to explain and demonstrate the concepts of truncation, rounding, overflow, and conversion error.

1. 1.17
10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Truncation, Rounding,
Overflow, and
Conversion Error
MATH1003

2. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Goal
To be able to explain and demonstrate the concepts of
truncation, rounding, overflow, and conversion error.
MATH1003

3. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
The computer is imperfect
MATH1003

4. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
The computer is imperfect
No matter how large a computer is, it still has a limited
amount of storage.
MATH1003

5. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
The computer is imperfect
No matter how large a computer is, it still has a limited
amount of storage.
Consider the result of dividing 2 by 3.
2/
MATH1003
3

6. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
The computer is imperfect
No matter how large a computer is, it still has a limited
amount of storage.
Consider the result of dividing 2 by 3.
0.666666 is a repeating number.
2/
MATH1003
3

7. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
The computer is imperfect
No matter how large a computer is, it still has a limited
amount of storage.
Consider the result of dividing 2 by 3.
0.666666 is a repeating number.
Regardless of how many bits we use to store this
number, it will get “cut off” at some point. No computer
can accurately store this number.
2/
MATH1003
3

8. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Truncation
2/
MATH1003
3

9. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Truncation
To truncate a number means to simply ignore the extra
digits that the computer cannot store.
2/
MATH1003
3

10. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Truncation
To truncate a number means to simply ignore the extra
digits that the computer cannot store.
Truncate the following to 3 significant digits
0.2349
2/
MATH1003
3

11. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Truncation
To truncate a number means to simply ignore the extra
digits that the computer cannot store.
Truncate the following to 3 significant digits
0.234
2/
MATH1003
3

12. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Truncation
To truncate a number means to simply ignore the extra
digits that the computer cannot store.
Truncate the following to 5 significant digits
0.666666666666
2/
MATH1003
3

13. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Truncation
To truncate a number means to simply ignore the extra
digits that the computer cannot store.
Truncate the following to 5 significant digits
0.66666
2/
MATH1003
3

14. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Truncation
To truncate a number means to simply ignore the extra
digits that the computer cannot store.
Truncate the following to 8 significant binary digits
0.1010101111000101
2/
MATH1003
3

15. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Truncation
To truncate a number means to simply ignore the extra
digits that the computer cannot store.
Truncate the following to 8 significant binary digits
0.10101011
2/
MATH1003
3

16. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Real Numbers
0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0
Represent 0.02510 in IEEE standard
1. 0.02510 = 0.00000112 0.000001100110011
1.100110011001
1.1001 x 2-6
2. normalized as 1.1001 x 2-6
3. set the sign bit
4. store -6 in the exponent section as (-6 + 127 = 121) 011110012
5. store the normalized binary form
MATH1003

17. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Overflow Error
MATH1003

18. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Overflow Error
Let’s assume that we are using 8 bits and 2’s complement
to store integers (1 sign bit and 7 bits for the number).
MATH1003

19. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Overflow Error
Let’s assume that we are using 8 bits and 2’s complement
to store integers (1 sign bit and 7 bits for the number).
Calculate 12610 + 1310
MATH1003

20. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Overflow Error
Let’s assume that we are using 8 bits and 2’s complement
to store integers (1 sign bit and 7 bits for the number).
Calculate 12610 + 1310
12610
+ 1310
MATH1003

21. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Overflow Error
Let’s assume that we are using 8 bits and 2’s complement
to store integers (1 sign bit and 7 bits for the number).
Calculate 12610 + 1310
12610 011111102
+ 1310 +000011012
MATH1003

22. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Overflow Error
Let’s assume that we are using 8 bits and 2’s complement
to store integers (1 sign bit and 7 bits for the number).
Calculate 12610 + 1310
12610 011111102
+ 1310 +000011012
100010112
MATH1003

23. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Overflow Error
Let’s assume that we are using 8 bits and 2’s complement
to store integers (1 sign bit and 7 bits for the number).
Calculate 12610 + 1310
12610 011111102
+ 1310 +000011012
bit n
sig
100010112
MATH1003

24. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Overflow Error
Let’s assume that we are using 8 bits and 2’s complement
to store integers (1 sign bit and 7 bits for the number).
Calculate 12610 + 1310
12610 011111102 this is -11710 in
2’s complement, but
the answer should be
+ 1310 +000011012 13910.
What happened?
bit n
sig
100010112
MATH1003

25. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Overflow Error
Let’s assume that we are using 8 bits and 2’s complement
to store integers (1 sign bit and 7 bits for the number).
Calculate 12610 + 1310
12610 01111110sign 7 bits can only store
Remember that the
first bit is used as a
2
+ 1310
up to 127.
+000011012
bit.
bit n
sig
100010112
MATH1003

26. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Overflow Error
Let’s assume that we are using 8 bits and 2’s complement
to store integers (1 sign bit and 7 bits for the number).
Calculate 12610 + 1310
12610 011111102 7 bits can only
store up to 127.
+ 1310
We have an overflow
+000011012 problem.
bit n
sig
100010112
MATH1003

27. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Rounding
2/
MATH1003
3

28. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Rounding
An alternative to truncation is rounding, where the last
digit is “adjusted” to give a more accurate representation
of the number.
2/
MATH1003
3

29. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Rounding
An alternative to truncation is rounding, where the last
digit is “adjusted” to give a more accurate representation
of the number.
Round the following to 2 significant digits
2/
MATH1003
3

30. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Rounding
An alternative to truncation is rounding, where the last
digit is “adjusted” to give a more accurate representation
of the number.
Round the following to 2 significant digits
2.53
2/
MATH1003
3

31. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Rounding
An alternative to truncation is rounding, where the last
digit is “adjusted” to give a more accurate representation
of the number.
Round the following to 2 significant digits
2.53
2/
MATH1003
3

32. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Rounding
An alternative to truncation is rounding, where the last
digit is “adjusted” to give a moreSince 3 is less than 5,
accurate representation
of the number. will be like
this
truncation
Round the following to 2 significant digits
2.53
2/
MATH1003
3

33. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Rounding
An alternative to truncation is rounding, where the last
digit is “adjusted” to give a moreSince 3 is less than 5,
accurate representation
of the number. will be like
this
truncation
Round the following to 2 significant digits
2.5
2/
MATH1003
3

34. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Rounding
An alternative to truncation is rounding, where the last
digit is “adjusted” to give a more accurate representation
of the number.
Round the following to 2 significant digits
2.5
2/
MATH1003
3

35. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Rounding
An alternative to truncation is rounding, where the last
digit is “adjusted” to give a more accurate representation
of the number.
Round the following to 3 significant digits
17.948
2/
MATH1003
3

36. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Rounding
An alternative to truncation is rounding, where the last
digit is “adjusted” to give a more accurate representation
of the number.
Round the following to 3 significant digits
17.948
2/
MATH1003
3

37. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Rounding
An alternative to truncation is rounding, where the last
digit is “adjusted” to give a more accurate representation
Since 4 is less than 5,
of the number.this will be like
truncation
Round the following to 3 significant digits
17.948
2/
MATH1003
3

38. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Rounding
An alternative to truncation is rounding, where the last
digit is “adjusted” to give a more accurate representation
of the number.
Round the following to 3 significant digits
17.9
2/
MATH1003
3

39. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Rounding
An alternative to truncation is rounding, where the last
digit is “adjusted” to give a more accurate representation
of the number.
Round the following to 2 significant digits
-0.002463
2/
MATH1003
3

40. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Rounding
An alternative to truncation is rounding, where the last
Since we are
digit is “adjusted” to give a more accurate representation
concerned only
about the significant
of the number. digits, we will only
consider these
Round the following to 2 significant digits
digits
-0.002463
2/
MATH1003
3

41. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Rounding
An alternative to truncation is rounding, where the last
digit is “adjusted” to give a more accurate representation
of the number.
Round the following to 2 significant digits
-0.002463
2/
MATH1003
3

42. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Rounding
An alternative to truncation is rounding, where the last
digit is “adjusted” to give a more accurate 6representation
Since is greater
than or equal to 5, we
of the number.“round up” the 4 to its
left to 5
Round the following to 2 significant digits
-0.002463
2/
MATH1003
3

43. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Rounding
An alternative to truncation is rounding, where the last
digit is “adjusted” to give a more accurate representation
of the number.
Round the following to 2 significant digits
-0.0025
2/
MATH1003
3

44. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Rounding
An alternative to truncation is rounding, where the last
digit is “adjusted” to give a more accurate representation
of the number.
Round the following to 5 significant digits
0.173
2/
MATH1003
3

45. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Rounding
An alternative to truncation is rounding, that this isthe last
Note where a
repeating number.
digit is “adjusted” to give a more accurateexpand to at least
We should
representation
of the number. significant digits before
6
rounding to 5 significant
Round the following to 5 significant digits
digits
0.173
2/
MATH1003
3

46. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Rounding
An alternative to truncation is rounding, that this isthe last
Note where a
repeating number.
digit is “adjusted” to give a more accurateexpand to at least
We should
representation
of the number. significant digits before
6
rounding to 5 significant
Round the following to 5 significant digits
digits
0.173737
2/
MATH1003
3

47. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Rounding
An alternative to truncation is rounding, where the last
digit is “adjusted” to give a more accurate representation
of the number.
Round the following to 5 significant digits
0.173737
2/
MATH1003
3

48. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Rounding
An alternative to truncation is rounding, where the last
digit is “adjusted” to give a more accurate representation
of the number.
Round the following to 5 significant digits
0.173737
2/
MATH1003
3

49. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Rounding
An alternative to truncation is rounding, where the last
digit is “adjusted” to give a more accurate representation
Since 7 is greater
than or equal to 5, we
of the number. “round up” the 3 to its
left to 4
Round the following to 5 significant digits
0.173737
2/
MATH1003
3

50. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Rounding
An alternative to truncation is rounding, where the last
digit is “adjusted” to give a more accurate representation
of the number.
Round the following to 5 significant digits
0.17374
2/
MATH1003
3

51. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Conversion Error
Let’s represent 0.110 with 4 bytes in IEEE standard form.
0.1
MATH1003

52. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Conversion Error
Let’s represent 0.110 with 4 bytes in IEEE standard form.
1. 0.110 = 0.000112
0.1
MATH1003

53. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Conversion Error
Let’s represent 0.110 with 4 bytes in IEEE standard form.
1. 0.110 = 0.000112
2. normalize 0.000112 = 1.10011 x 2-4
0.1
MATH1003

54. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Conversion Error
Let’s represent 0.110 with 4 bytes in IEEE standard form.
1. 0.110 = 0.000112 1.10011 x 2-4
2. normalize 0.000112 = 1.10011 x 2-4
0.1
MATH1003

55. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Conversion Error
Let’s represent 0.110 with 4 bytes in IEEE standard form.
1. 0.110 = 0.000112 1.10011 x 2-4
2. normalize 0.000112 = 1.10011 x 2-4
3. set the sign bit
0.1
MATH1003

56. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Conversion Error
0
Let’s represent 0.110 with 4 bytes in IEEE standard form.
1. 0.110 = 0.000112 1.10011 x 2-4
2. normalize 0.000112 = 1.10011 x 2-4
3. set the sign bit
0.1
MATH1003

57. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Conversion Error
0
Let’s represent 0.110 with 4 bytes in IEEE standard form.
1. 0.110 = 0.000112 1.10011 x 2-4
2. normalize 0.000112 = 1.10011 x 2-4
3. set the sign bit
4. store -4 in the exponent section
0.1
MATH1003

58. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Conversion Error
0
Let’s represent 0.110 with 4 bytes in IEEE standard form.
1. 0.110 = 0.000112 1.10011 x 2-4
2. normalize 0.000112 = 1.10011 x 2-4
3. set the sign bit -4 + 127 = 123
4. store -4 in the exponent section
123 = 011110112
0.1
MATH1003

59. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Conversion Error
0 0 1 1 1 1 0 1 1
Let’s represent 0.110 with 4 bytes in IEEE standard form.
1. 0.110 = 0.000112 1.10011 x 2-4
2. normalize 0.000112 = 1.10011 x 2-4
3. set the sign bit -4 + 127 = 123
4. store -4 in the exponent section
123 = 011110112
0.1
MATH1003

60. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Conversion Error
0 0 1 1 1 1 0 1 1
Let’s represent 0.110 with 4 bytes in IEEE standard form.
1. 0.110 = 0.000112 1.10011 x 2-4
2. normalize 0.000112 = 1.10011 x 2-4
3. set the sign bit
4. store -4 in the exponent section
5. store the normalized binary form
0.1
MATH1003

61. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Conversion Error
0 0 1 1 1 1 0 1 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0
Let’s represent 0.110 with 4 bytes in IEEE standard form.
1. 0.110 = 0.000112 1.10011 x 2-4
2. normalize 0.000112 = 1.10011 x 2-4
3. set the sign bit
4. store -4 in the exponent section
5. store the normalized binary form
0.1
MATH1003

62. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Conversion Error
0 0 1 1 1 1 0 1 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0
0.1
MATH1003

63. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Conversion Error
0 0 1 1 1 1 0 1 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0
Now, let’s convert this back to decimal
0.1
MATH1003

64. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Conversion Error
0 0 1 1 1 1 0 1 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0
Now, let’s convert this back to decimal
1. since the sign bit is 0, we know this is a positive number
0.1
MATH1003

65. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Conversion Error
0 0 1 1 1 1 0 1 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0
Now, let’s convert this back to decimal
1. since the sign bit is 0, we know this is a positive number
2. the exponent section is 01111011 (= 123)
0.1
MATH1003

66. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Conversion Error
0 0 1 1 1 1 0 1 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0
Now, let’s convert this back to decimal
1. since the sign bit is 0, we know this is a positive number
2. the exponent section is 01111011 (= 123)
3. the decimal exponent is 123 - 127 = -4
0.1
MATH1003

67. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Conversion Error
0 0 1 1 1 1 0 1 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0
Now, let’s convert this back to decimal
1. since the sign bit is 0, we know this is a positive number
2. the exponent section is 01111011 (= 123)
3. the decimal exponent is 123 - 127 = -4
4. from the number section, we have 1.10011001100110011001100
0.1
MATH1003

68. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Conversion Error
0 0 1 1 1 1 0 1 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0
Now, let’s convert this back to decimal
1. since the sign bit is 0, we know this is a positive number
2. the exponent section is 01111011 (= 123)
3. the decimal exponent is 123 - 127 = -4
4. from the number section, we have 1.10011001100110011001100
5. therefore the number is 1. 10011001100110011001100 x 2-4
0.1
MATH1003

69. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Conversion Error
0 0 1 1 1 1 0 1 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0
Now, let’s convert this back to decimal
1. since the sign bit is 0, we know this is a positive number
2. the exponent section is 01111011 (= 123)
3. the decimal exponent is 123 - 127 = -4
4. from the number section, we have 1.10011001100110011001100
5. therefore the number is 1. 10011001100110011001100 x 2-4
6. 1. 10011001100110011001100 = 1.59999990463 (approximately)
0.1
MATH1003

70. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Conversion Error
0 0 1 1 1 1 0 1 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0
Now, let’s convert this back to decimal
1. since the sign bit is 0, we know this is a positive number
2. the exponent section is 01111011 (= 123)
3. the decimal exponent is 123 - 127 = -4
4. from the number section, we have 1.10011001100110011001100
5. therefore the number is 1. 10011001100110011001100 x 2-4
6. 1. 10011001100110011001100 = 1.59999990463 (approximately)
7. 1.59999990463 x 2-4 = 0.099999994
0.1
MATH1003

71. 10110100101011010100101010111010101111011011101111011101110111101110111011110111111010110100101011110110110101111011010100111111011010100110101001
Conversion Error
0 0 1 1 1 1 0 1 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0
Now, let’s convert this back to decimal
1. since the sign bit is 0, we know this is a positive number
2. the exponent section is 01111011 (= 123) This is a
3. the decimal exponent is 123 - 127 = -4 conversion error:
4. from the number section, we have 1.10011001100110011001100
0.099999994 ≠ 0.1
5. therefore the number is 1. 10011001100110011001100 x 2-4
6. 1. 10011001100110011001100 = 1.59999990463 (approximately)
7. 1.59999990463 x 2-4 = 0.099999994
0.1
MATH1003