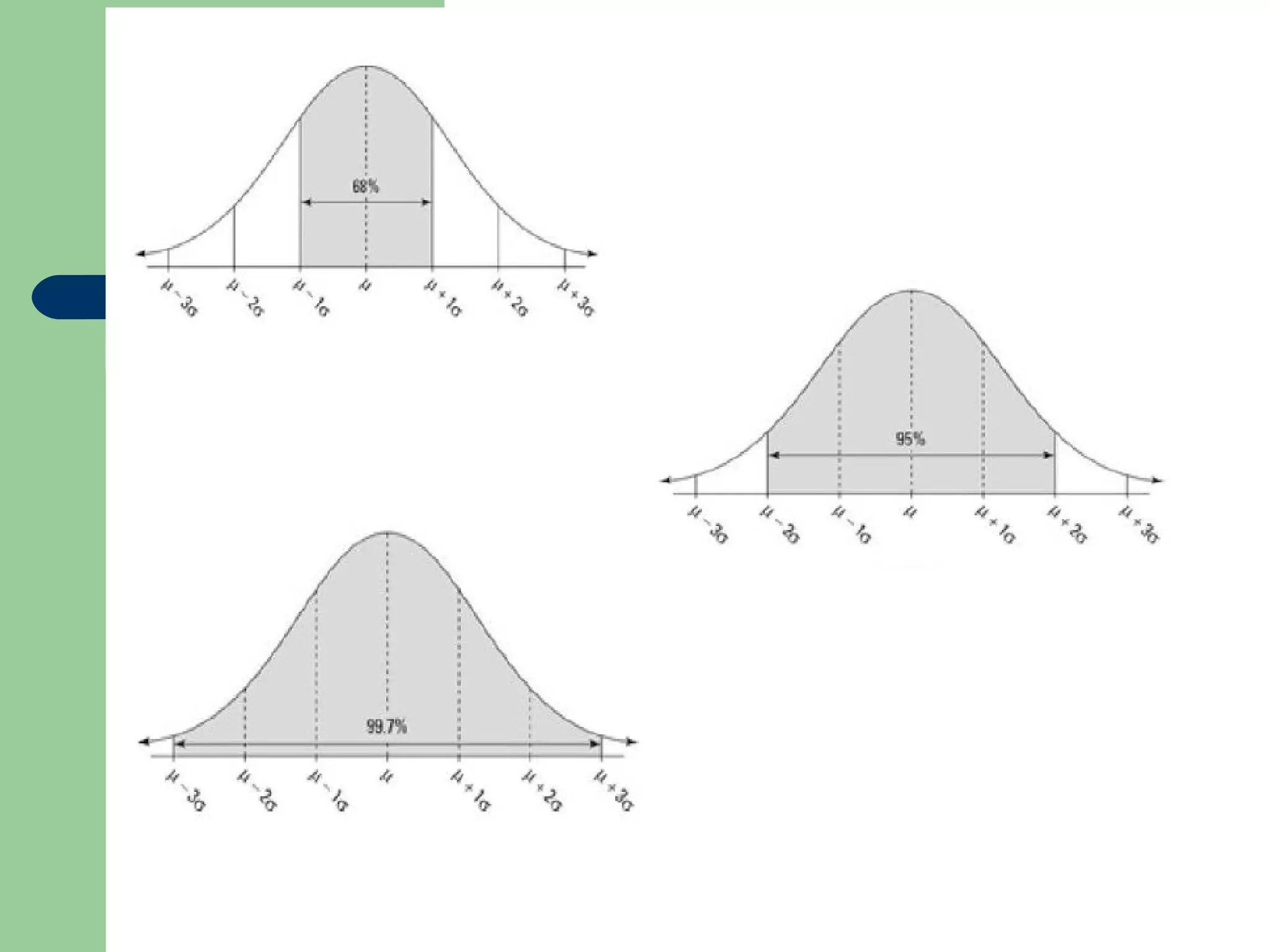
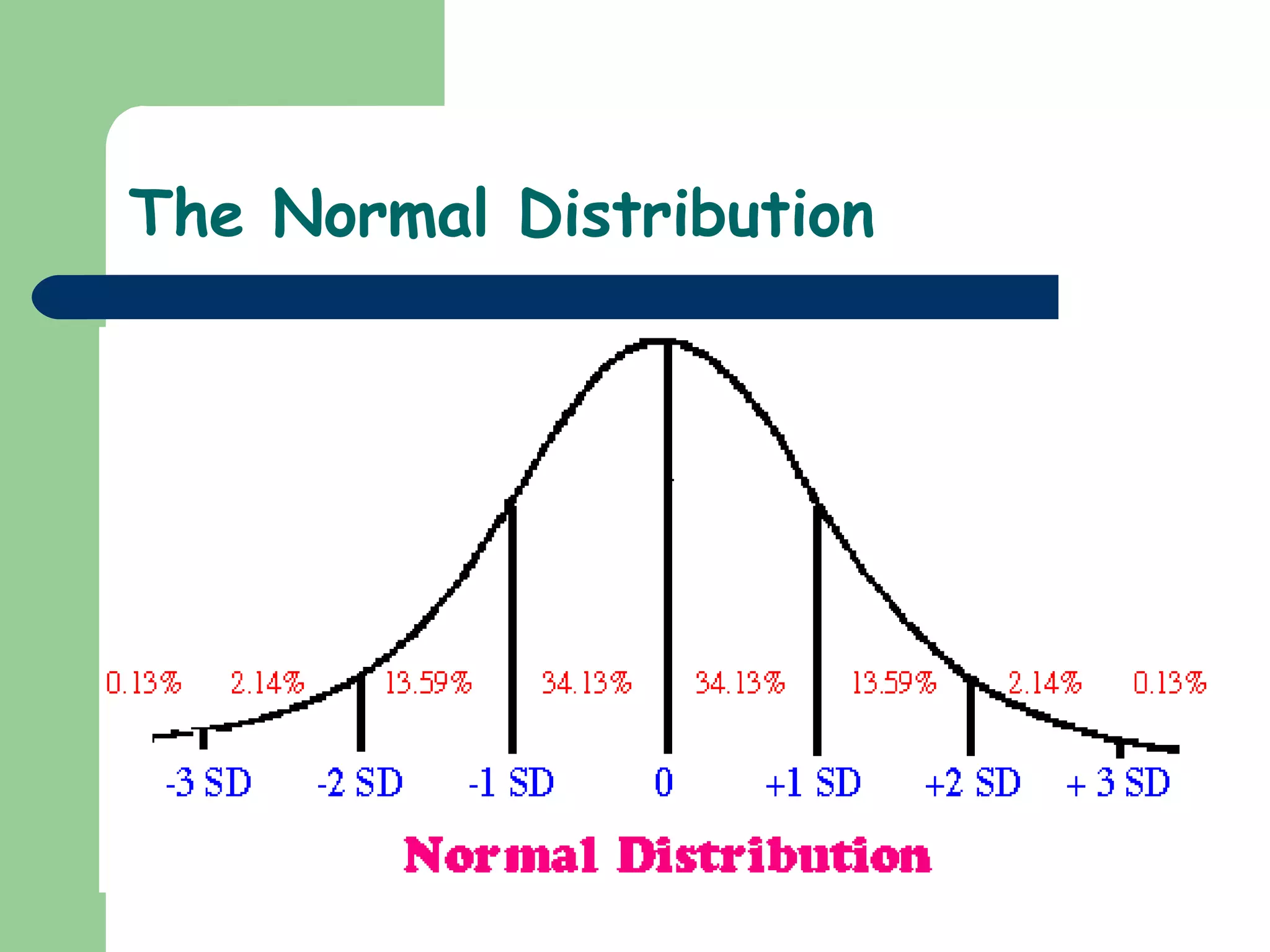
The document discusses the normal distribution and statistical hypothesis testing. It notes that the normal distribution is also called the Gaussian distribution, and has equal mean, median and mode. It then discusses how much of the data falls within standard deviations of the mean for the normal distribution. The document also covers confidence intervals for means, the steps of statistical hypothesis testing including assumptions, hypotheses, significance levels and tests, and different statistical tests used for numerical and categorical data like t-tests, ANOVA, regression and correlation.

1. The Normal Distribution
Also called Gaussean Distribution.
Mean = Median = Mode.
Skewness = zero & Kurtosis =
zero.
Total area under the curve = 1.

3. The Normal Distribution

4. The Normal Distribution, cont.
 68% of observations lie between minus & plus
one SD. ( -1Z & +1Z ).
 95% of observations lie between minus 1.96 &
plus 1.96 SD units.
 99% of observations lie between minus 2.58 &
plus 2.58 SD units.
 99.7% of observations lie between minus 3 &
plus 3 SD units.

5. Confidence interval for a mean
 The range with in which the population mean
is likely to lie.
s.d.
95% C.I. = X ± 1.96
√n
s.d.
99% C.I. = X ± 2.58
√n

6. Confidence interval for a mean
If n ≤ 30
s.d.
C.I. = X ± t
√n

7. Steps of testing the statistical
hypothesis
*Assumption
We assume that our population(s) are
normally distributed.
*Hypothesis
We put null hypothesis (Ho) &
alternative hypothesis (HA).

8. *Levels of significance (alpha)
Alpha = the probability of rejecting a true
null hypothesis.
Usually alpha = 0.05 or 0.01
*Degrees of freedom (d.f.): Depends on
the type of the statistical test.
*The statistics
Depends on type of data.

9. *Statistical decision
Whether to reject or not to reject Ho.
*P value
Whether < or > 0.05
(or whether P < or > 0.01)

10. Tests of Statistical Significance
Depending on the type of data, an
appropriate test will be used.
Generally speaking, Data are either
numerical or categorical data.

11. • For Numerical data; we usually compute
the mean & it’s standard deviation.
• In order to test whether there is a
significant difference between two means
related to two different groups, we use
the student (t) test.
The t test is also used to compare
between two sets of data within the same
group ie. To compare between two readings
for the same person but on two occasions,
eg. Before & after treatment.

12. *To compare between several means; we
use the analysis of variance (ANOVA, or
called the F test); & when we have
several numerical variables & one of
them is dependent on the others
(independent variables) then we use the
multiple regression.

13. *In order to examine the nature & strength of
the relationship between two variables ( e.g..
Blood pressure & age), simple linear regression
& correlation tests are used.
*The objective of regression analysis is to
predict (estimate) the value of one variable
corresponding to a given value of another
variable.

14. *Correlation analysis is concerned with measuring
the strength of the relationship between
variables.