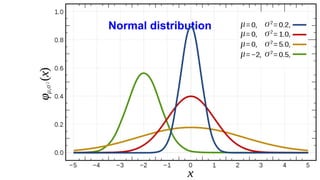
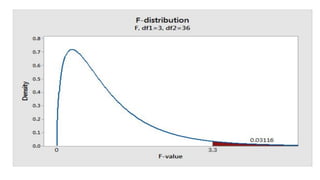
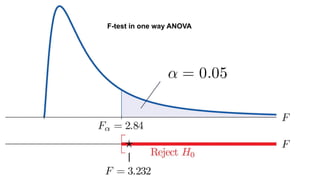
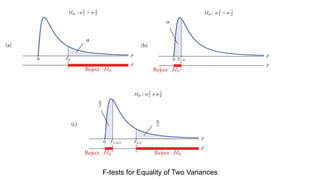
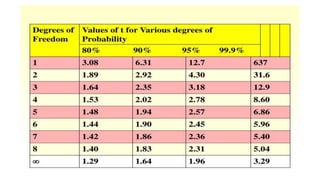
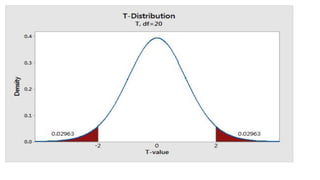
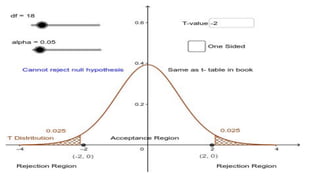
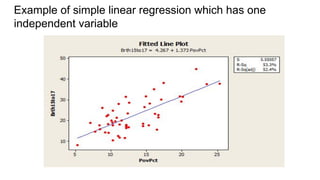
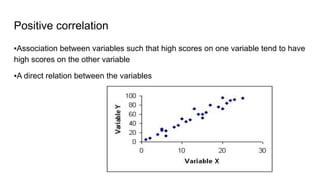
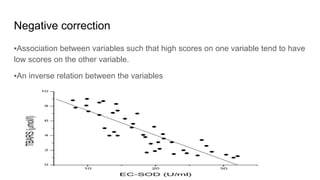
The document discusses the application of statistical methods in pharmaceutical analysis, covering topics like normal distribution, confidence intervals, t-tests, ANOVA, regression analysis, and the correlation coefficient. It highlights the importance of these methods in evaluating drug efficacy, comparing different treatments, and analyzing data in the pharmaceutical industry. Additionally, it provides insights into specific tests for analyzing data sets, including the rejection of outliers using the q-test.

1. Rohan Jagdale
Pharmaceutical Analysis II
T. Y. B. Pharm
YTIP, UNIVERSITY OF MUMBAI
STATISTICAL DATA
HANDLING

2. Contents
❏ Introduction
❏ Normal distribution
❏ Confidence limits
❏ F-test
❏ T-test (paired & unpaired)
❏ Linear regression analysis
❏ Correlation coefficient
❏ Rejection of data (Q test)

3. Introduction
Pharmaceutical statistics is the application of statistics to matters concerning the
pharmaceutical industry. This can be from issues of design of experiments, to analysis of
drug trials, to issues of commercialization of a medicine.
▪Evaluate the activity of a drug; e.g.; effect of caffeine on attention; compare the analgesic
effect of a plant extract and NSAID
▪To explore whether the changes produced by the drug are due to the action of drug or by
chance NOR
▪To compare the action of two or more different drugs or different dosages of the same
drug are studied using statistical methods.
▪To find an association between disease and risk factors such as Coronary artery disease
and smoking

4. Normal distribution

5. Normal distribution, also known as the Gaussian distribution, is
a probability distribution that is symmetric about the mean,
showing that data near the mean are more frequent in
occurrence than data far from the mean. In graph form, normal
distribution will appear as a bell curve.
For example, heights, blood pressure, measurement error, and
IQ scores follow the normal distribution. It is also known as the
Gaussian distribution and the bell curve.

6. Confidence limit
● Two extreme measurements within which an
observation lies
● End points of the confidence interval
● Laraer confidence-
● A measure of the reliability (Re)
● The reliability of a mean ( x) increases as more
measurements are taken
● R=k(n)1/2
● Reliability increases with square root of number of
measurements
● Quickly reach a condition of limiting return

7. A point estimate is a single number
A confidence interval contains a certain set of possible values of
the parameter.
Lower confidence limit Point estimate Upper confidence limit
Width of confidence

8. Confidence Intervals and the Normal Distribution
A confidence interval is a range of values that gives the user a sense of how
precisely a statistic estimates a parameter. The most familiar use of a confidence
interval is likely the "margin of error" reported in news stories about polls: "The
margin of error is plus or minus 3 percentage points." But confidence intervals are
useful in contexts that go well beyond that simple situation.
Confidence intervals can be used with distributions that aren't normal—that are
highly skewed or in some other way non-normal. But it's easiest to understand what
they're about in symmetric distributions, so the topic is introduced here. Don't let that
get you thinking that you can use confidence intervals with normal distributions only.

9. F - Test or Analysis of variance (ANOVA)
An “F Test” is a catch-all term for any test that uses the F-distribution. In
most cases, when people talk about the F-Test, what they are actually
talking about is The F-Test to Compare Two Variances. However, the
f-statistic is used in a variety of tests including regression analysis, the
Chow test and the Scheffe Test (a post-hoc ANOVA test).
An F-test is any statistical test in which the test statistic has an
F-distribution under the null hypothesis. It is most often used when
comparing statistical models that have been fitted to a data set, in order to
identify the model that best fits the population from which the data were
sampled.

10. Why do we use F-test?
Because we want to find out if there is a significant difference between and among
the means of the two ore more independent groups.
When do we use F-Test?
when there is normal distribution and when the level of measurement
is expressed in interval or ratio data just like t-test and the z-test.

13. F-test in one way ANOVA

14. F-tests for Equality of Two Variances

15. Student’s t-test / t-test
The Student's t-Test was formulated by W.Gossett in the early 1900's.
His employer (brewery) had regulations concerning trade secrets that
prevented him from publishing his discovery, but in light of the
importance of theet distribution, Gossett was allowed to publish under
the pseudonym "Student".
The t-Test is typically used to compare the means of two populations

16. t = (Xi - u) / s
● t depends on desired confidence limit
● degrees of freedom (N-1)
● One uses this test when the population variance is
unknown, as is usually the case in the social sciences.
● The standard error of the sampling distribution of the
sample mean is estimated.
● At distribution is used to create confidence intervals, like
critical values.

20. The t - formula

21. Paired t test
Samples happens to be small
Variances of the two populations need not be equal
Populations are nomal
may be one sided or two sided

22. Unpaired t- test
The unpaired t method tests the null hypothesis that the population means related
to two independent, random samples from an approximately normal distribution
are equal (Altman, 1991; Armitage and Berry, 1994).
Assuming equal variances, the test statistic is calculated as:

23. t test applications
The T-test is used to compare the mean of two samples, dependent or
independent.
It can also be used to determine if the sample mean is different from the assumed
mean.
T-test has an application in determining the confidence interval for a sample mean.

24. Regression
A statistical measure that attempts to determine the strength of
the relationship between one dependent variable (usually
denoted by Y) and series of other changing variables (known as
independent variables).
Forecast value of a dependent variable (Y) from the value of
independent variables (X1, X2,...).

25. Regression Analysis
In statistics, regression analysis includes many techniques for
modeling and analyzing several variables, when the focus is on
the relationship between a dependent variable and one or more
independent variables.
Regression analysis is widely used for prediction and
forecasting,

26. Dependant and independant variable
▪Independent variables are regarded as inputs to a system and may take
on different values freely.
▪Dependent variables are those values that change as a consequence of
changes in other values in the system.
▪Independent variable is also called as predictor or explanatory variable
and it is denoted by X.
▪Dependent variable is also called as response variable and it is denoted
by Y.

27. Linear regression
▪The simplest mathematical relationship between two variables x
and y is a linear relationship.
▪In a cause and effect relationship, the independent variable is the
cause, and the dependent variable is the effect.
▪Least squares linear regression is a method for predicting the
value of a dependent variable Y, based on the value of an
independent variable X.

29. Example of simple linear regression which has one
independent variable

30. Correlation Coefficient

31. Defination
Correlation refers to technique used to measure the relafionship between
two or more variables.
A correlation coefficient is a statistical measure of the degree to which
changes to the valUe of one variable predict change to the value of
another.
A corelation can only indicate the presence or absence of a relationship,
not the nature of the relationship. Correlation is not causation.

32. Correlation Coefficient formula overview
Correlation Coefficient formula are used to find how strong a
relationship is between data. The formulas return a value
between-1 and 1, where:
▪1 indicates a strong positive relationship.
▪-1 indicates a strong negative relationship.
▪A result of zero indicates no relationship at all

34. Positive correlation
▪Association between variables such that high scores on one variable tend to have
high scores on the other variable
▪A direct relation between the variables

35. Negative correction
▪Association between variables such that high scores on one variable tend to have
low scores on the other variable.
▪An inverse relation between the variables

36. Correlation Coefficient formula
▪One of the most commonly used formulas in statistic is Pearson's correlation
coefficient formula.

37. Rejection of data /Q test / Dixon’s Q test
It is a statistical test for deciding if an outlier can be
removed from a set of data. It is used for small data
sets.
It is simpler to apply, as it does not require
calculation of the mean and standard deviation.

38. Rejection of result (Q test)
● Used for small data sets
● 90% CL is typically used
● Arrange data in increasing order
● Calculate range = highest value - lowest value
● Calculate gap |suspected value - nearest valuel
● Calculate Q ratio = gap/range
● Reject outlier if Qcal> Qtab
● Q tables are available

40. Example:: Is 167 an outlier in this set of data? Test at the 95%
confidence Level (i.e. at an alpha level of 5%).
167, 180, 188, 177, 181, 185, 189
Step 1: Sort your data into ascending order (smallest to largest).
167, 177, 180, 181, 185, 188, 189.
Step 2 :Find the Q statistic using the following formula:
dixon's q test statistic
Where:
x1 is the smallest (suspect) value,
x2 is the second smallest value,
and xn is the largest value.

41. Inserting the values into the formula, we get:
Q = (177 – 167) / 189 – 167 = 10/22 = 0.455.
Step 3: Find the Q critical value in the Q table (scroll to the bottom of the article for the
table). For a sample size of 7 and an alpha level of 5%, the critical value is 0.568.
Step 4: Compare the Q statistic from Step 2 with the Q critical value in Step 3. If the Q
statistic is greater than the Q critical value, the point is an outlier.
Qstatistic = 0.455.
Qcritical value = 0.568.
Solution: 0.455 is not greater than 0.568, so this point is not an outlier at an alpha level of
5%.