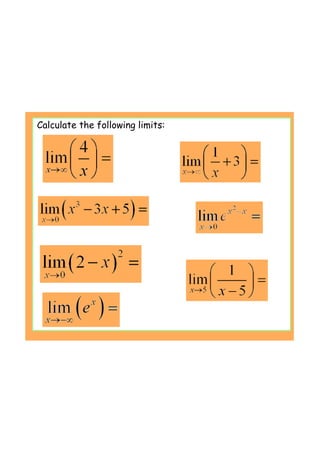
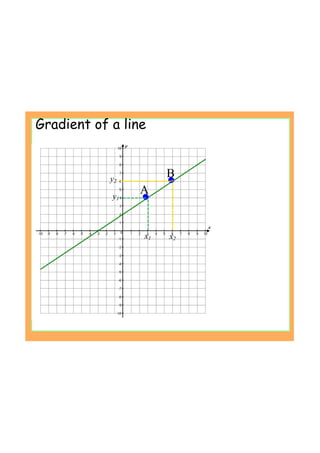
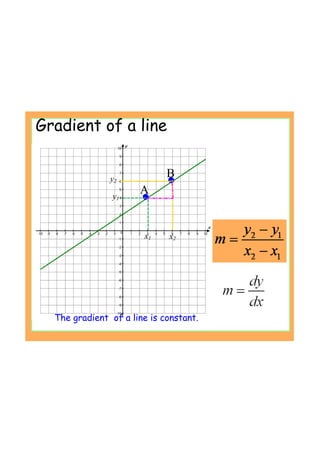
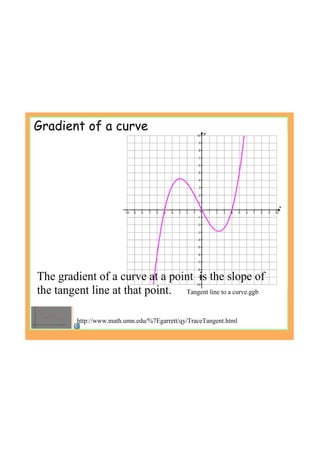
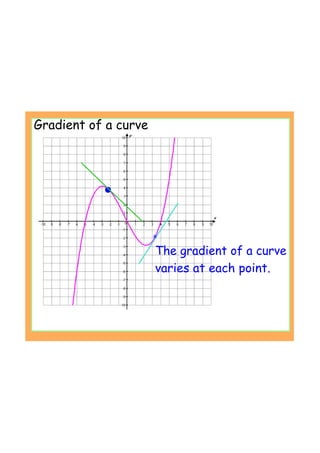
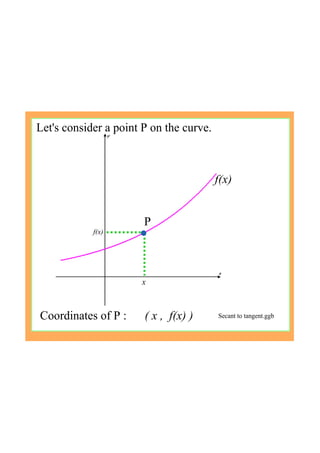
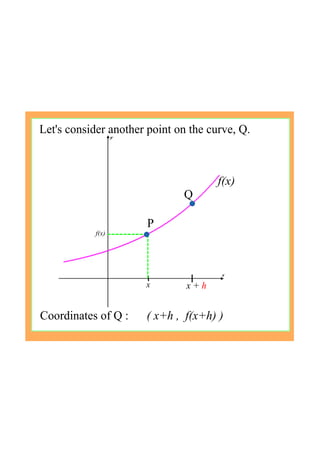
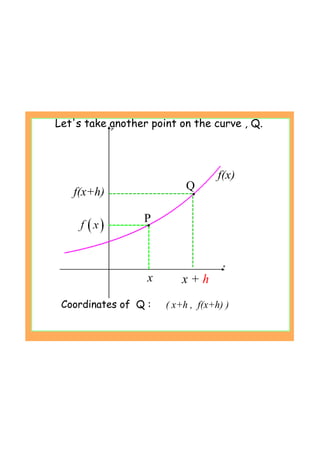
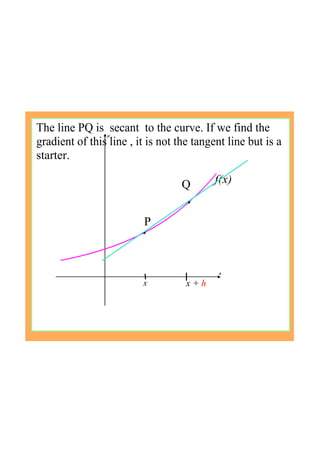
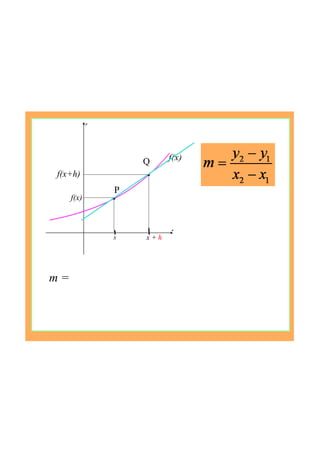
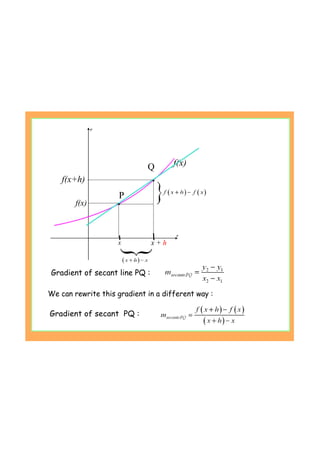
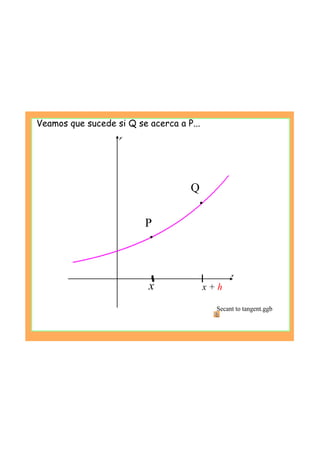
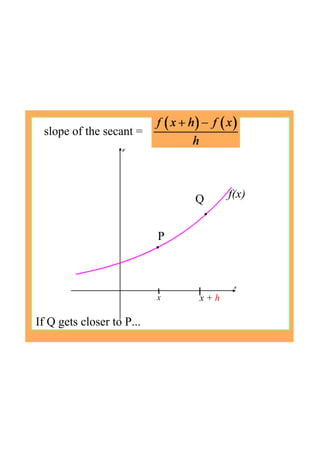
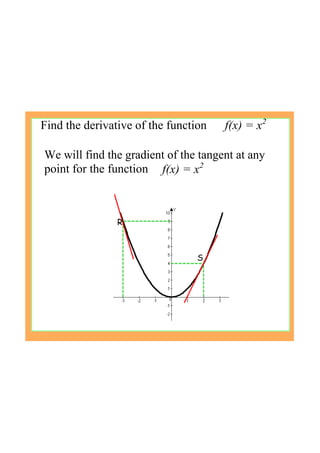
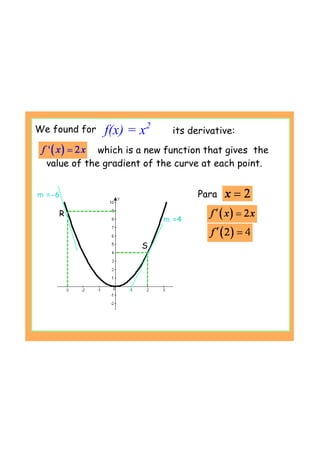
This document provides an introduction to the concept of differentiation by explaining how to calculate the gradient of a curve at a given point. It defines the derivative as the limit of the difference quotient as the change in x approaches 0. This represents the slope of the tangent line. The document demonstrates calculating the derivative of basic functions like f(x)=x^2 from first principles and provides additional online resources for practice.

2. Calculate the following limits:

3. By the end of the lesson you will be able to:
• Understand the definition of derivative.
• Find derivatives from first principles.
Differentiation
• Calculate the gradient of a curve without drawing
the tangent line.
• Relate derivatives and slopes of curves.

4. Introduction to Differentiation
http://www.youtube.com/watch?v=QC5ITOflh3k&feature=related

5. Gradient of a line
B
A

6. Gradient of a line
B
A
y2
y1
x1 x2

7. Gradient of a line
B
A
y2
y1
x1 x2
The gradient of a line is constant.

8. Gradient of a curve
The gradient of a curve at a point is the slope of
the tangent line at that point.
http://www.math.umn.edu/%7Egarrett/qy/TraceTangent.html
Tangent line to a curve.ggb

9. Gradient of a curve
The gradient of a curve
varies at each point.

10. We need to find a method to calculate the slope of
the tangent line at any point.

11. x
Let's consider a point P on the curve.
P
f(x)
Coordinates of P : ( x , f(x) )
f(x)
Secant to tangent.ggb

12. Coordinates of Q : ( x+h , f(x+h) )
x
Let's consider another point on the curve, Q.
P
f(x)
Q
x + h
f(x)

13. Coordinates of Q : ( x+h , f(x+h) )
x
Let's take another point on the curve , Q.
P
Q
x + h
f(x+h)
f(x)

14. x
The line PQ is secant to the curve. If we find the
gradient of this line , it is not the tangent line but is a
starter.
P
f(x)Q
x + h

15. x
P
f(x)Q
x + h
f(x)
f(x+h)
m =

16. x
P
f(x)Q
x + h
f(x)
f(x+h)
Gradient of secant line PQ :
We can rewrite this gradient in a different way :
Gradient of secant PQ :

17. Q
x + h
Veamos que sucede si Q se acerca a P...
P
x
Secant to tangent.ggb

18. slope of the secant =
x
P
f(x)Q
x + h
If Q gets closer to P...

19. Then we need h to be as small as possible.
h 0When the slope of the secant tends to
be the slope of the tangent.
This is the difference quotient , the definition of
the derivative.

20. This is called
the first derivative of function f with respect to x.
Notation:
f '(x) or y' or

21. Find the derivative of the function f(x) = x2
Pp
R
S
We will find the gradient of the tangent at any
point for the function f(x) = x2

22. f(x) = x 2

23. Pp
R
S
m =4
m =-6
We found for f(x) = x2
which is a new function that gives the
value of the gradient of the curve at each point.
Para
its derivative:

24. Calculate the derivative of f(x) = 3 x2
+1
To practice this topic on-line :
http://archives.math.utk.edu/visual.calculus/2/definition.7/index.html

25. The process of finding the derivative is called
differentiation.

26. Book page 357 Ex 12B
http://www.calculus­help.com/funstuff/phobe.html
At the end of the lesson:

27.
http://www.calculus­help.com/funstuff/phobe.html
To revise this lesson at home:

28. At the end of the lesson:
http://animoto.com/play/hVIw4sOG1tEL3hYONxJyJQ

29. Attachments
Tangent line to a curve.ggb
Secant to tangent.ggb