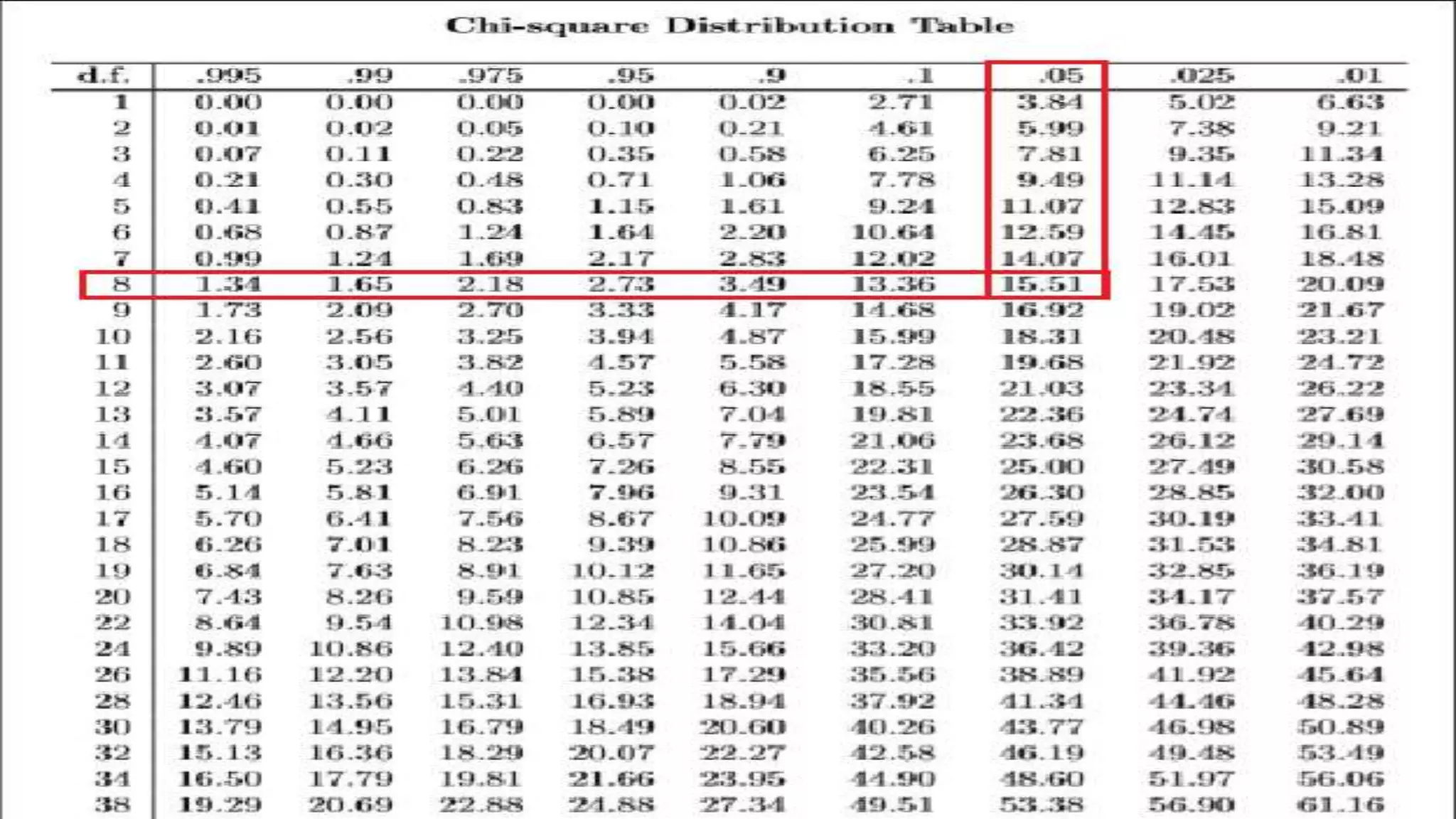
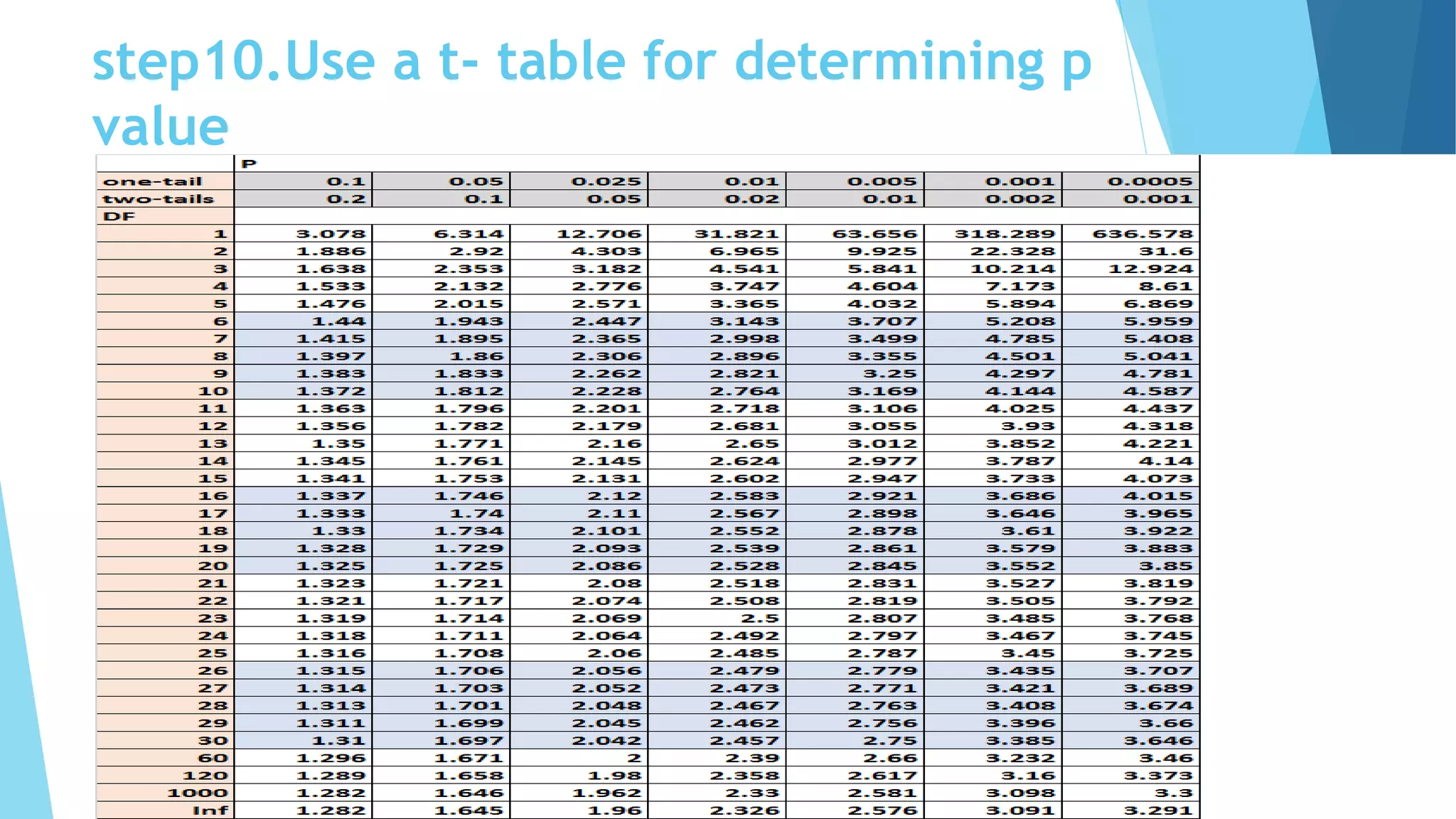
This document provides an overview of various statistical tests used for hypothesis testing, including parametric and non-parametric tests. It defines key terms like population, sample, mean, median, mode, and standard deviation. It explains the stages of hypothesis testing including creating the null and alternative hypotheses, determining the significance level, and deciding which statistical test to use based on the type of data and number of samples. Specific tests covered include the z-test, t-test, ANOVA, chi-square test, Wilcoxon signed-rank test, Mann-Whitney U test, Kruskal-Wallis test, and Friedman test.

1. TEST OF
SIGNIFICANCE
Dr Joice P Jiji
MDS first year
GUIDED BY
Dr Sandeep J N

2. contents
 Introduction
 Common terms in statistics
 Biostatistics
 Hypothesis –null and alternate
 Test of significance
 Parametric and non parametric tests
 Z- test
 Student t- test
 ANOVA
 Chi Square test

3.  Mc Nemar’s test
 The Wilcoxon signed-rank test
 Mann –Whitney U test
 The Kruskal Wallis test
 The Friedman tests
 Fisher's exact test
 Post hoc rank test
 Conclusion
 references

4. Introduction
Statistics is the discipline that concerns the collection,
organization, analysis, interpretation, and presentation of data
Statistics is an important and integral part of research
methodology. It is a pervasive force on which the entire
spectrum of clinical decision making is dependent

5. Test of significance are one of the
central concept in statistics
 These are mathematical method by
which the probability of an observed
difference occurring by chance is
found.

6. Common terms in
statistics

7. Variable: A characteristic that takes on
different values in different, places or
things. 2 types dependent and
independent variable
A dependent variable is the variable being
tested in a scientific experiment.
Examples of independent variables are
• Age, sex, race

8.  Population: It is an entire group of
people or study elements— persons, things
or measurements for which we have an
interest at a particular time. Populations
are determined by our sphere of interest.
It may be infinite or finite.

9.  Sampling unit: Each member of a
population.
 Sample: It may be defined as a part of a
population. It is a group of sampling units
that form part of a population, generally
selected so as to be representative of the
population whose variables are under
study. There are many kinds of sample
methods in Biostatistics.

10. Mean This measure implies arithmetic average or
arithmetic mean which is obtained by summing up
all the observations and dividing the total by the
number of observations.
Median When all the observations of a variable are
arranged in either ascending or descending order,
the middle observation is known as median
 Mode This is the most frequently occurring
observation in a se

11.  6mm,7 mm,4mm, 6mm,5 mm,6 mm,8 mm,4 mm
 Mean = 6+ 7+4+6+5+6+8 +4 = 46/8 = 5.75 mm
8
 Median = 4mm,4mm,5mm,6mm,6mm,6mm,7mm,8mm
 Median 6+6= 12/2= 6 mm
2
 Mode= 6mm
 4mm,4mm,5mm,6mm,6mm,6mm ,7mm,8mm

12. Normal distribution and Normal curve
• Gaussian distribution,
• First observed by Abraham de Moivre in
1733
• Probability distribution that is symmetric
about the mean.
• A theoretical , continuous, symmetrical
,unimodal distribution of infinite range
• Most of the biological variables follow
normal distribution

13.  The characteristics of a normal curve are:
 1. It is bell-shaped
 2. It is symmetrical.
 3. Mean, mode and median coincide. =0
 4. It has two inflections
 Total area is =1
 Standard deviation=1

15. STATISTICAL INFERENCE
Inference means drawing of conclusion from data
It is the process of drawing up conclusions from
quantitative or qualitative information using the
methods of statistics to describe and arrange the data
and to test suitable hypothesis
Statistical inference are based on probabilities and as
such cannot be expressed with full certainty

16. BIOSTATISTICS
Biostatistics is the term used when tools
of statistics are applied to the data that is
derived from biologic science such as
medicine
Statistical analysis is the back bone of
research

17. TEST OF SIGNIFICANCE
Whenever two sets of observation
are compared, it become essential
to find out whether difference
observed between the two group is
because of sampling variation or any
other factor

18. STAGES IN PERFORMING A TEST OF
SIGNIFICANCE
1 Create a null hypothesis
2 Create an alternative hypothesis
3 Determine the significance level
4 Decide on the test we will use
5 Perform a power analysis to find
out your sample size

19. 6 calculate the standard deviation
7 Use the standard deviation
8 Determine the t- score(F,H,P,U)
9 Find the degree of freedom
10.Use a t- table for determining p
value

20. In Statistics, a hypothesis is defined as a formal
statement, which gives the explanation about the
relationship between the two or more variables of the
specified population. It helps the researcher to translate
the given problem to a clear explanation for the outcome
of the study.
What is a hypothesis ???
20

21. CHARECTERISTICS OF HYPOTHESIS
1. Hypothesis should be clear and precise.
2. Hypothesis should be capable of being
tested.
3. It should state relationship between
variables.

22. 4 It must be specific.
5 It should be stated as simple as
possible.
6 It should be amenable to testing
within a reasonable time.
7 It should be consistent with
known facts.

23. classification
Based on their formulation
Null hypothesis and alternate
hypothesis

24. Null hypothesis
It states that there is no real difference between the
means (or proportions ) of the groups being compared
(or that there is no real association between two
continuous variables).
It is denoted by Ho.
Example- “ There is no difference in the clinical
attachment level with treatment A or treatment B”.

25. Step 2 Alternate hypothesis
 If null hypothesis is rejected, we need another
hypothesis…..an alternate hypothesis.
 It states that there must be a true difference
between the groups being compared.
 It is denoted by HA or Ha or H1.
 Example- “there is a difference in the clinical
attachment gain with treatment A and
treatment B”.

26. In Hypothesis testing we proceed on the basis of Null
Hypothesis. We always keep Alternative Hypothesis
in mind.
It seems strange to begin the process by asserting that
something is not true, but it is far easier to disprove
an assertion than to prove that something is true.
The Null Hypothesis and the Alternative Hypothesis
are chosen before the sample is drawn.

27. Step 3 Determining LEVEL OF
SIGNIFICANCE
 Before the study is started, we have to establish a
criterion called level of significance or alpha level which
is the highest risk of making a false positive error of
rejecting the null hypothesis that the investigator is
willing to accept.
 So the confidence with which the null hypothesis is
rejected or accepted is called as Level of significance
 A common alpha is 0.05 or 5%

28. The higher the significance level used for
testing a hypothesis, the higher the
probability of rejecting null hypothesis,
when it is true.
If P value is less than alpha ,we will reject
null hypothesis
If P value is more than or equal to alpha we
will not reject null hypothesis

29. STEP 4 Decide which test we have to use?
Parametric tests
• Their model specifies
certain condition about
the parameters of the
population from the
research sample is drawn
• Used for quantitative data
Non- parametric tests
• Their model does not
specify condition about
the parameters of which
the research sample is
drawn
• Used for qualitative data

30. Quantitative (or Continuous) Data
The quantitative data have a magnitude. The
characteristics is measured either on an
interval or on a ratio scale.
It got a numerical value
Age
Height, weight
RAL

31. Qualitative (or Discrete) Data
In such data there is no notion of
magnitude or size of the characteristic
or attribute as the same cannot be
measured.
 Young and old
 Gender
 Social class
 Redness of gingiva
 Efficacy of drug

32. Parametric tests Non parametric test
Paired t-test Wilcoxon signed rank test
Unpaired t-test
Z test
Mann-Whitney U-test
Chi square test
One way ANOVA Kruskal Wallis test
Fischer exact probability
test
Repeated ANOVA Friedman test

33. 1 large sample tests
 When the sample size is greater than 30
 Generally ,2 types of data may be
encountered while testing hypothesis for large
samples
 When data is qualitative -------- test for
proportion( chi square /x2 test)
 When data is quantitative -------- test for
means(z-test )

34.  2. small sample tests
 When the sample size is smaller than 30
 Sample does not follow the normal distribution
,hence it is based on the assumption that the
population from which the sample is drawn follows
the normal distribution
 Student T test
unpaired and paired
 ANOVA
 Chi-square test(pronounced as kye)

35. Choice of an appropriate statistical
significance test to be used
 Association between two variables---- chi-square test
 Correlation between two variables ----- pearson’s or
spearman’s test
 One group on two occasions-------paired test
 One group on 3 or more occasions------------------ ANOVA
 Two separate groups------------unpaired t test, Mann-Whitney
u test
 3 or more separate groups--------ANOVA

36. step 6- Standard deviation
The standard deviation is the most
important and widely used measure of
studying dispersion.
It is also known as root mean square
deviation
Small standard deviation means a higher
degree of uniformity of observation
Standard deviation expressed with sigma s

37. Formula to caculate standard deviation
s
6mm,7 mm,4mm, 6mm,5 mm,6 mm,8 mm,4 mm
Mean = 6+ 7+4+6+5+6+8 +4 = 46/8 = 5.75 mm
8
SD s = 1.38873

38. Student’s t-test
Designed by W.S Gosette, whose pen name was
Student
t is ratio of observed difference between two
means of small samples to the standard error of
difference in the same
Sample here should be less than 30

39. t= difference between two means
S.E of difference between two means
T test
Paired t test
Unpaired t test
(independent or unmatched
or pooled t test)

40. Paired test- e.g clinical attachment loss(CAL)
before and after scaling
Unpaired t-test e.g. effect or scaling in males
and females ,The mean PI, GI, PD & CAL
between 02 groups at different time intervals.

41.  UNPAIRED T TEST-Steps
1 Hypothesis
2 find the observation difference between means of
two samples (x1-x 2)
3 calculate the standard error (SE) of difference
between the two means
4. Calculate t value t= (x1-x 2)
SE
SE= s root of 1/n1 + 1/n2
s - standard deviation

42. PAIRED T TEST-Steps
1 null hypothesis
2 find the observed difference in each set
paired observations before and after of
the same sample(x1-x2=x)
3 calculate mean of the differences
4 workout the standard error of the mean
5. Calculate the t value

44. Z test (standard normal test)
z test is done when the population is more than
30 for quantitative data
Used to compare :
1. Two sample means
2. Sample mean with population mean
3. Two sample proportions
4. Sample proportion with population
proportion

45. X- sample average
m- mean
s- standard deviation

46. ANOVA
Analysis of variance(F test)
Developed by Professor R A Fisher
Analysis of variance is useful to assess
the significance of difference of
differences between sample means
which are more than two in number

47. If the independant variable quantitative and
categorical (i.e. nominal, dichomatous, ordinal) the
correct multivariable technique is ANOVA

48. One way ANOVA
If the design include one independent variable
that technique is called one way ANOVA,
regardless of how many different groups are
compared.
Another term for one-way ANOVA is F- test.
F-test is a kind of super t-test that allows the
investigator to allow more than two means
simultaneously.

49. The ratio of the between group variance to
the within groups variance is called F(in honor
of Fischer).
F= s2
1 based on variation between the group
s2
2 based on variation between the group

50. Two way ANOVA
 More than one independent variable present eg
treatment plan A and B , age, sex
 The goal of ANOVA is to explain as much variation
in the continuous variable as possible, by using
one or more categorical variables to predict the
variation………..
 In this the impact of two different factors on the
variations in a specific variable is tested.
 Two way ANOVA is also called N way ANOVA

51. The chi square test for
quantitative data
Chi square test is used for
comparing a sample variance to
population variance
x2 = s2
s (n-1)
s2
p

53. Non parametric test
1.Chi square test for qualitative data ,developed by
karl pearson
Used to test the association between two events (to
test a given hypothesis)
e.g. cause and effect like tobacco use and cancer
Χ2 = ∑ (Oi – Ei)2/Ei
Oi observed frequencies Ei excepted frequencies
Frequency means the no of times the value occurrs in the data

54. Paired samples--The Wilcoxon signed-
rank test
Also known as matched pair test
It is a non-parametric statistical
hypothesis test
used either to test the location of a
population based on a sample of data, or
to compare the locations of two
populations using two matched
samples. Like more aggressive and less aggressive

56. 3.unpaired samples -Mann –Whitney U
test
A non parametric test used to compare the
medians of two independent sample.it is the
non parametric equivalent of the t test
e.g, GCF GF levels between 2 groups at
different time interval

57. U=n1 n2 + n1(n1+n2) - R1
2
U=Mann-Whitney U test
n1 = sample size one
n2= Sample size two Ri =
Rank of the sample size

58. 4. Fisher's exact test
Fisher's exact test used in the analysis
of contingency tables. Although in practice it
is employed when sample sizes are small, it
is valid for all sample sizes.
Inventor- Ronald Fisher, and is one of a class
of exact tests

59. Success and failure in group 1 and 2

60. 5.McNemar’s test
A variant of chi squared test ,used when
the data is paired
it can be used to analyze retrospective
case-control studies, where each case is
matched to a particular control. Or it can be
used to analyze experimental studies,
where the two treatments are given to
matched subjects.

61. 6.The Kruskal Wallis test
 The Kruskal Wallis test is the non parametric alternative
to the One Way ANOVA.
 The H test is used when the assumptions for ANOVA
aren’t met (like the assumption of normality). It is
sometimes called the one-way ANOVA on ranks, as the
ranks of the data values are used in the test rather than
the actual data points.
 The test determines whether the medians of two or more
groups are different.

62. 7. The Friedman test
developed by Milton Friedman
The Friedman test is used for one-way
repeated measures analysis of variance by
ranks. In its use of ranks it is similar to
the Kruskal–Wallis one-way analysis of
variance by ranks.
The Friedman test is widely supported by
many statistical software packages.

63. Post-hoc test (multiple comparisons)
 “AFTER THIS”
 For comparison of three or more group means
we apply the analysis of variance (ANOVA)
method to decide if all means are equal or there
is at least one means are equal or there is at
least one mean which is different from others. If
we get significant result we can conclude that
there is difference in group means
 To know what specific pairs of group means
show differences-Post-hoc test (multiple
comparisons) procedures.

64. The set of comparison is referred as
a family of test
Bonferroni correction- safe option
Turkey’s HSD procedures- assumption met
Scheffe's procedures
Newman –keuls procedures
Dunnette’s procedures

65. Step 9 calculating Degree of
freedom
 No of independent members in the
sample
 The degrees of freedom formula is
straightforward. Calculating the degrees
of freedom is often the sample size minus
the number of parameters you’re
estimating:

66. step10.Use a t- table for determining p
value

67. The level of statistical significance is often expressed as
a p -value between 0 and 1. The smaller the p-value, the
stronger the evidence that you should reject the null
hypothesis.
 A p -value less than 0.05 (typically 0.05) is statistically
significant.
If P value is less than alpha ,we will reject null
hypothesis
If P value is more than or equal to alpha we will
not reject null hypothesis

68. Computer in biostatical analysis
The MINITAB ,SPSS,SAS and STATA are the
some well known statistical software
packages for personal computer which are
used for the tabulation and statistical
analysis of data
SPSS(Statistical Package for the Social Sciences) is
commonly used

69. Limitations of test of significance
1.Test are only useful aids for decision making
not decision making itself
2.Do not explain why does the difference exist
3. Result are based on probabilities and such
cannot expressed in full certainty
4.Inferences based on them cannot be said to
be entirely correct evidence connecting truth
of the hypothesis

70. Conclusion
 Tests of significance play an important role in conveying the results of
any research and thus the choice of an appropriate statistical test is
very important aa it decides the fate of out come of the study
 The tests are only useful aids for decision-making. Hence “proper
interpretation of statistical evidence is important to intelligent
decisions.”
 If the data deviate strongly from the assumptions of a parametric
procedure, using the parametric procedure could lead to incorrect
conclusions.

71. References
 Soben Peter Community Dentistry 6th Edition.
 Text book methods in bio statistics 7th edt. B K Majajan
 Jain S, Gupta A, Jain D. Common statistical tests in dental
research. Journal of Advanced Medical and Dental Sciences
Research. 2015 Jul 1;3(3):38.
 Joseph john Preventive and community dentistry 2nd edt

72. My sincere thanks to
 DR ARUNA D R
 DR VINAYAK S GOWDA
 DR AVINASH J L
 DR RAJIV N P
 DR REKHA JAGADEESH
 DR SANDEEP J N
 DR SOWMYA PRAVEEN
 ALL MY POST GRADUATE COLLEGUES

73. Previous seminar questions
 COMPONENTS OF LA
 Local anaesthetic drug ----lignocaine hydrochloride
 Vasopressor/vasoconstrictor drug---------Adrenalin
 Preservatives-methylparaben, thymol, chlorbutol
 Sodium chloride/Ringer’s solution
 Distilled water
 General preservative
 Alternative for methylparaben---sodium bisulfite,
metabisulfite

74. Short acting corticosteroid

75. Anaphylaxis- treatment
1. The first thing to do is to stop injection of allergen.
2. Call for help, check patient's vitals
3. Use 0.5ml ml of 0.1% of epinephrine intravenously.
4. If the patient pressure would not stabilize after 15
minutes, repeat this procedure. max 3 times
5. corticosteroids are very useful for such cases. IV OR
IM(prednisone, dexamethasone and hydrocortisone)
6. If a patient has signs of asphyxiation you should make an
injection of aminophylline 2.4% – 10-20 ml intravenously
7. Shift the patient to near hospital as early as possible

76. Signs and symptoms of anaphylactic
shock
•feeling lightheaded or faint.
•breathing difficulties – such as fast, shallow breathing.
•wheezing.
•a fast heartbeat.
•clammy skin.
•confusion and anxiety.
•collapsing or losing consciousness. hypotension
Skin reactions, including hives and itching and flushed or
pale skin.

77. Blood loss during flap surgery
 Ariaudo 1970 observed that a full mouth flap
surgery under general anesthesia blood loss is
around 300 ml.
 According to D A Baab 59.47+or-38.2ml
 Berdon -gingivectomies involving 5 to 14 teeth -5
ml to 149 ml
 According to Mclvor and Wengraf -10 fold increase
in blood loss per tooth during periodontal flap than
gingivectomies

78. Other names of lignocaine
Lidocaine
Brand name xylocaine