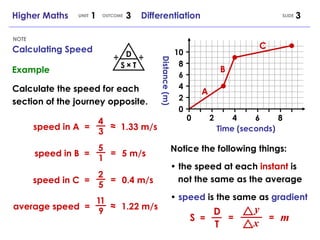
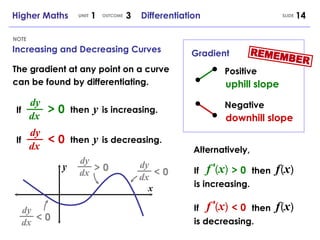
The document discusses differentiation and its history. It was independently developed in the 17th century by Isaac Newton and Gottfried Leibniz. Differentiation allows the calculation of instantaneous rates of change and is used in many areas including mathematics, physics, engineering and more. Key concepts covered include calculating speed, estimating instantaneous rates of change, the rules for differentiation, and differentiation of expressions with multiple terms.