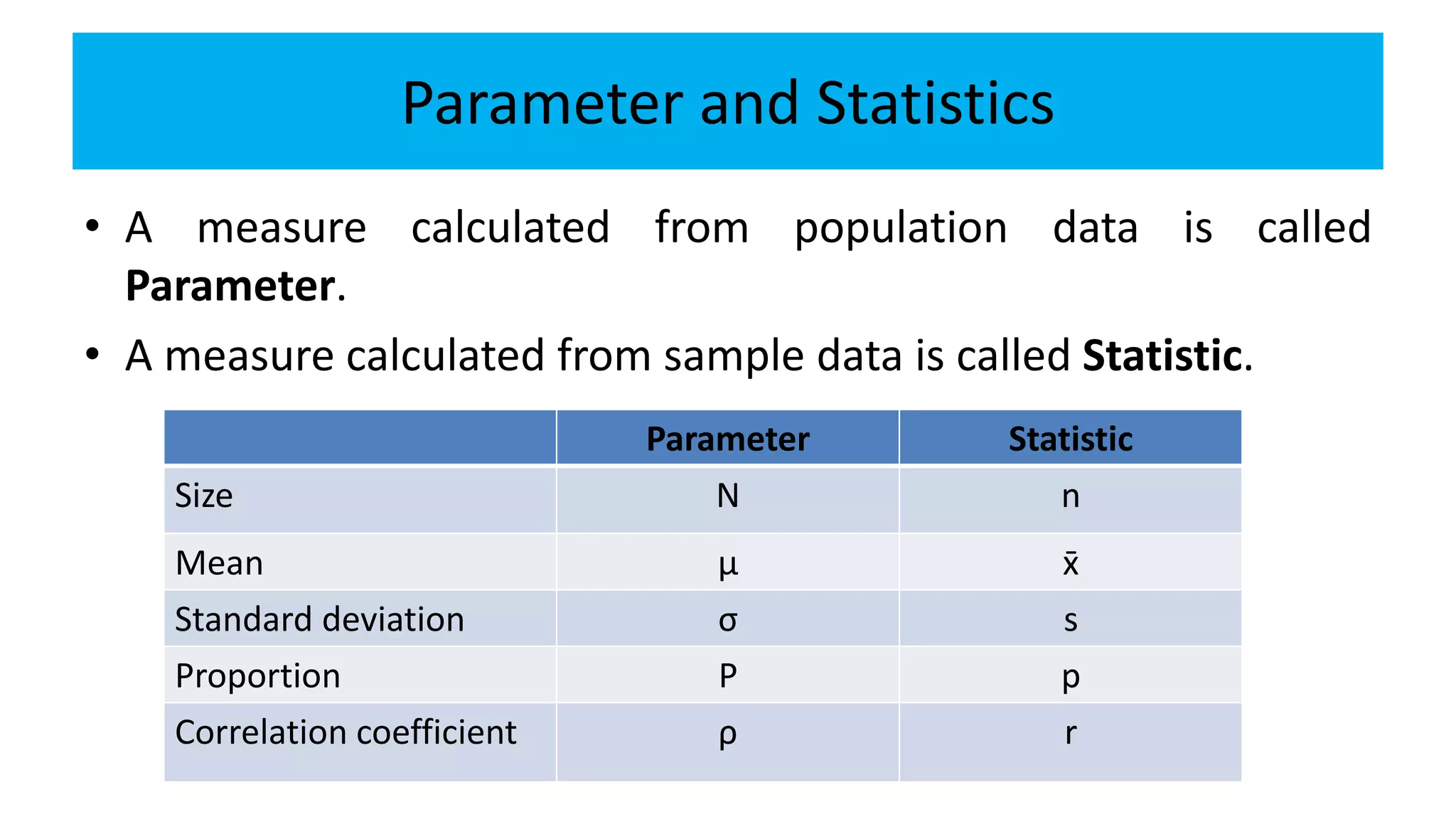
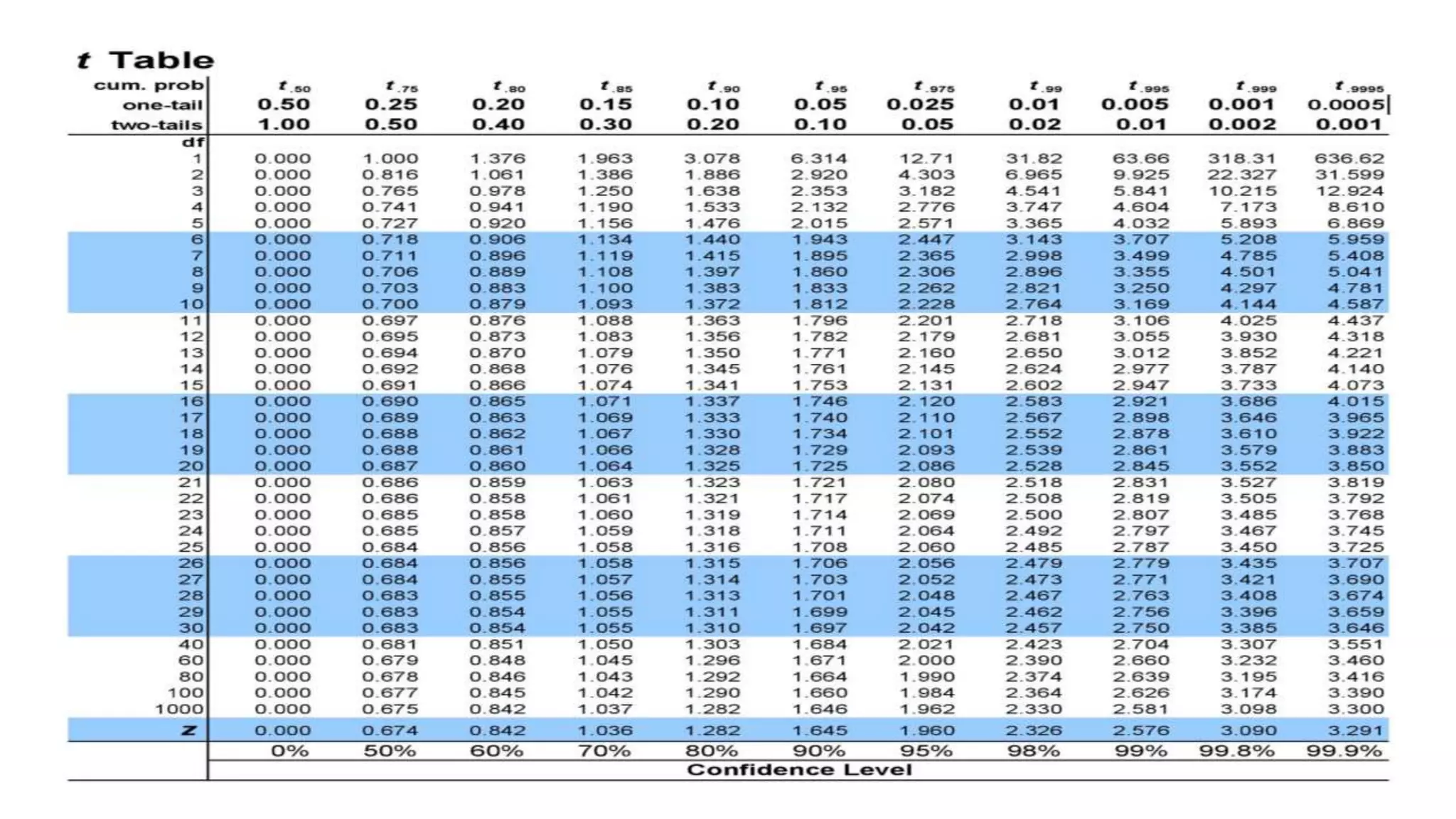
The document discusses statistical inference, specifically the distinction between parameters (population data) and statistics (sample data), emphasizing methods like estimation and hypothesis testing. It outlines the characteristics of good estimators, various estimation techniques including point and interval estimation, and the calculation of standard errors for different statistical measures. Additionally, it provides case studies to illustrate confidence intervals for means and proportions, aiding in understanding of how statistical methods are applied in real-world scenarios.

1. STATISTICAL INFERENCE:
ESTIMATION

2. Parameter and Statistics
• A measure calculated from population data is called
Parameter.
• A measure calculated from sample data is called Statistic.
Parameter Statistic
Size N n
Mean μ x̄
Standard deviation σ s
Proportion P p
Correlation coefficient ρ r

3. Statistical Inference
The method to infer about population on the basis of sample
information is known as Statistical inference.
It mainly consists of two parts:
• Estimation
• Testing of Hypothesis

4. Estimation
Estimation is a process whereby we select a random sample from
a population and use a sample statistic to estimate a population
parameter.
There are two ways for estimation:
• Point Estimation
• Interval Estimation

5. Point Estimate
Point Estimate – A sample statistic used to estimate the exact
value of a population parameter.
• A point estimate is a single value and has the advantage of
being very precise but there is no information about its
reliability.
• The probability that a single sample statistic actually equal to
the parameter value is extremely small. For this reason point
estimation is rarely used.

6. Good Estimator
Properties of good estimator:
1. Unbiasedness
2. Consistency
3. Sufficiency
4. Efficiency

7. Unbiasedness
Any sample statistic is said to be an unbiased estimator for the
population parameter if on an average the value sample statistic
is equal to the parameter value.
e.g. 𝐸 𝑥 = 𝜇 i.e. sample mean is an unbiased estimator of
population mean

8. Consistency
An estimator is said to be a consistent estimator for the
parameter if the value of statistics gets closer to the value of the
parameter and the respective variance of statistics get closer to
zero as sample size increases.
e.g. 𝐸 𝑥 → 𝜇 and 𝑉 𝑥 =
𝜎2
𝑛
→ 0 as sample size n increases

9. Sufficiency
If a statistic contain almost all information regarding the
population parameter that is contained in the population then
the statistic is called sufficient estimator for the parameter.

10. Efficiency
An estimator is said to be an efficient estimator if it contains
smaller variance among all variances of all other estimators.

11. Interval Estimate
Confidence interval (interval estimate) – A range of values
defined by the confidence level within which the population
parameter is estimated to fall.
• The interval estimate is less precise, but gives more
confidence.

12. Example of Point and Interval Estimate
Government wants to know the percentage of cigarette smokers
among college students.
If we say that there was 10% are smokers, it is a point estimate.
But if we make a statement that 8% to 12% of college students
are smokers, it is interval estimate.

13. Sampling distribution
From a population of size N, number of samples of size n can be
selected and these samples give different values of a statistics.
These different values of statistic can be arranged in form of a
frequency distribution which is known as sampling distribution
of that statistics.
We can have sampling distribution of sample mean, sampling
distribution of sample proportion etc.

14. Standard Error of a statistics
The standard deviation calculated from the observations of a
sampling distribution of a statistics is called Standard Error of
that statistics.
E.g. The standard deviation calculated from the observations of
sampling distribution of x̄ is called standard error of x̄. It is
denoted by S.E.(x̄)

15. Standard Error for Mean
when population standard deviation (𝜎) is known
S.E.( 𝑥 ) =
𝜎
𝑛
for infinite population
S.E.( 𝑥 ) =
𝜎
𝑛
∗
𝑁−𝑛
𝑁−1
for finite population

16. Standard Error for Mean
when population standard deviation (𝜎) is unknown
When sample size is large ( n > 30)
S.E.( 𝑥 ) =
𝑠
𝑛
for infinite population
S.E.( 𝑥 ) =
𝑠
𝑛
∗
𝑁− 𝑛
𝑁−1
for finite population
When sample size is small ( n ≤ 30)
S.E.( 𝑥 ) =
𝑠
𝑛−1
for infinite population
S.E.( 𝑥 ) =
𝑠
𝑛−1
∗
𝑁− 𝑛
𝑁−1
for finite population

17. Standard Error for difference between two means
when population standard deviation (𝜎) is known
S.E.(𝑥1 − 𝑥2) =
𝜎1
2
𝑛1
+
𝜎2
2
𝑛2

18. Standard Error for difference between two means
when population standard deviation (𝜎) is unknown
When sample size is large ( n > 30)
S.E.(𝑥1 − 𝑥2) =
𝑠1
2
𝑛1
+
𝑠2
2
𝑛2
When sample size is small ( n ≤ 30)
S.E.(𝑥1 − 𝑥2) = 𝑠2(
1
𝑛1
+
1
𝑛2
)
Where
𝑠2 =
𝑛1∗𝑠1
2+𝑛2∗𝑠2
2
𝑛1+𝑛2−2

19. Standard Error for Proportion
S.E. (𝑝) =
𝑃𝑄
𝑛
for infinite population
S.E. (𝑝) =
𝑃𝑄
𝑛
𝑁−𝑛
𝑁−1
for finite population
When population proportion (𝑃) is unknown, then it is estimated by sample
proportion (𝑝)

20. Standard Error for difference between two proportions
Population proportions are known
S.E.(𝑝1 − 𝑝2) =
𝑃1 𝑄1
𝑛1
+
𝑃2 𝑄2
𝑛2
Population proportions are unknown
S.E.(𝑝1 − 𝑝2) = 𝑃 ∗ 𝑄 (
1
𝑛1
+
1
𝑛2
)
where
𝑃 =
𝑛1 𝑝1 + 𝑛2 𝑝2
𝑛1 + 𝑛2

21. Interval Estimation
Confidence Interval has the form:
Point estimate ± Margin of error
Where
Margin of error = Critical value of estimate * Standard Error of estimate

22. z table value
1 % 5% 10%
Two tailed test (≠ ) 2.58 1.96 1.645
One tailed test ( > or < ) 2.33 1.645 1.28

24. C.I. for Population mean
(i) When Population standard deviation is known or the sample
size is large
𝑥 ± 𝑍 𝛼 × S.E.( 𝑥 )
(ii) When Population standard deviation is unknown and the
sample size is small
𝑥 ± 𝑡 𝛼,𝑛−1 × S.E.( 𝑥 )

25. Case Study 1
A government agency was charged by the legislature with estimating the
length of time it takes citizens to fill out various forms. Two hundred
randomly selected adults were timed as they filled out a particular form.
The times required had mean 12.8 minutes with standard deviation 1.7
minutes.
Construct a 90% confidence interval for the mean time taken for all adults
to fill out this form.

26. Case Study 2
A thread manufacturer tests a sample of eight lengths of a
certain type of thread made of blended materials and obtains a
mean tensile strength of 8.2 lb with standard deviation 0.06 lb.
Assuming tensile strengths are normally distributed, construct a
90% confidence interval for the mean tensile strength of this
thread.

27. C.I. for difference between two means
(i) When Population standard deviation is known or the sample
size is large
(𝑥1 − 𝑥2) ± 𝑍 𝛼 × S.E.(𝑥1 − 𝑥2)
(ii) When Population standard deviation is unknown and the
sample size is small
(𝑥1 − 𝑥2) ± 𝑡 𝛼,𝑛1+𝑛2−2 × S.E.(𝑥1 − 𝑥2)

28. Case Study 1
Records of 40 used passenger cars and 40 used pickup trucks
(none used commercially) were randomly selected to investigate
whether there was any difference in the mean time in years that
they were kept by the original owner before being sold. For cars
the mean was 5.3 years with standard deviation 2.2 years. For
pickup trucks the mean was 7.1 years with standard deviation 3.0
years. Construct the 95% confidence interval for the difference in
the means based on these data.

29. Case Study 2
A university administrator wishes to know if there is a difference in average
starting salary for graduates with master’s degrees in engineering and those
with master’s degrees in business. Fifteen recent graduates with master’s
degree in engineering and 11 with master’s degrees in business are surveyed
and the results are summarized below. Construct the 99% confidence interval
for the difference in the population means based on these data.
n Mean Std. dev
Engineering 15 68,535 1627
Business 11 63,230 2033

30. C.I. for Population proportion
𝑝 ± 𝑍 𝛼 × S.E.(𝑝)

31. Case Study
In a random sample of 2,300 mortgages taken out in a certain
region last year, 187 were adjustable-rate mortgages. Assuming
that the sample is sufficiently large, construct a 99% confidence
interval for the proportion of all mortgages taken out in this
region last year that were adjustable-rate mortgages.

32. C.I. for difference between two proportions
(𝑝1 − 𝑝2) ± 𝑍 𝛼 × S.E.(𝑝1 − 𝑝2)

33. Case Study
A survey for anemia prevalence among women in developing
countries was conducted among African and Asian women. Out
of 2100 African women, 840 were anemia and out of 1900 Asian
women, 323 were anemia. Find a 95% confidence interval for the
difference in proportions of all African women with anemia and
all women from the Asian with anemia.