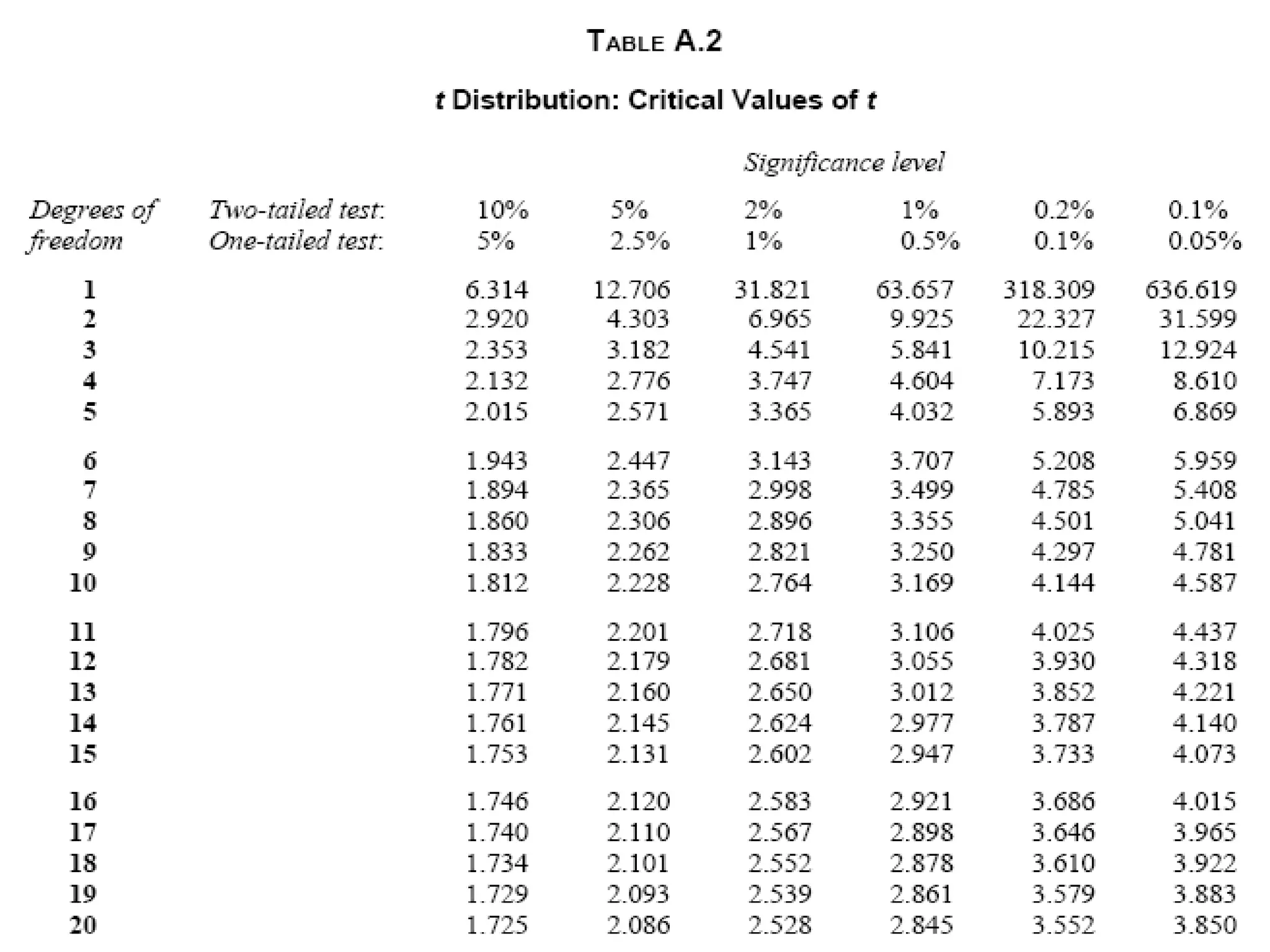
The t test can be used to compare sample means to population means, compare means between independent samples, or compare readings within a single sample taken at different times. It involves testing a hypothesis about whether two means are statistically significantly different. The document provides examples of applying the t test to compare a sample mean to a population mean, compare means between independent male and female samples, and compare blood pressure readings within a single sample taken before and after treatment.

1. 11
The t testThe t test

2. 22
ApplicationsApplications
 To compare the mean of a sample withTo compare the mean of a sample with
population mean.population mean.
 To compare the mean of one sampleTo compare the mean of one sample
with the mean of another independentwith the mean of another independent
sample.sample.
 To compare between the valuesTo compare between the values
(readings) of one sample but in 2(readings) of one sample but in 2
occasions.occasions.

3. 33
1.Sample mean and population1.Sample mean and population
meanmean
 The general steps of testing hypothesis must beThe general steps of testing hypothesis must be
followed.followed.
 Ho: Sample mean=Population mean.Ho: Sample mean=Population mean.
 Degrees of freedom = n - 1Degrees of freedom = n - 1
SE
X
t
−
−
=
µ

4. 44
ExampleExample
The following data represents hemoglobin values inThe following data represents hemoglobin values in
gm/dl for 10 patients:gm/dl for 10 patients:
Is the mean value for patients significantly differIs the mean value for patients significantly differ
from the mean value of general populationfrom the mean value of general population
(12 gm/dl) . Evaluate the role of chance.(12 gm/dl) . Evaluate the role of chance.
10.510.5 99 6.56.5 88 1111
77 7.57.5 8.58.5 9.59.5 1212

5. 55
SolutionSolution
 Mention all steps of testing hypothesis.Mention all steps of testing hypothesis.
Then compare with tabulated value, for 9 df, and 5% level ofThen compare with tabulated value, for 9 df, and 5% level of
significance. It is = 2.262significance. It is = 2.262
The calculated value>tabulated value.The calculated value>tabulated value.
Reject Ho and conclude that there is a statistically significant differenceReject Ho and conclude that there is a statistically significant difference
between the mean of sample and population mean, and thisbetween the mean of sample and population mean, and this
difference is unlikely due to chance.difference is unlikely due to chance.
352.5
10
80201.1
1295.8
−=
−
=t

6. 66

7. 77
2.Two independent samples2.Two independent samples
The following data represents weight in Kg for 10The following data represents weight in Kg for 10
males and 12 females.males and 12 females.
Males:Males:
Females:Females:
80 75 95 55 60
70 75 72 80 65
60 70 50 85 45 60
80 65 70 62 77 82

8. 88
2.Two independent samples, cont.2.Two independent samples, cont.
 Is there a statistically significant difference betweenIs there a statistically significant difference between
the mean weight of males and females. Let alpha =the mean weight of males and females. Let alpha =
0.010.01
 To solve it follow the steps and use this equation.To solve it follow the steps and use this equation.
)
11
(
2
)1()1(
2121
2
22
2
11
21
nnnn
SnSn
XX
t
+
−+
−+−
−
=
−
−

9. 99
ResultsResults
 Mean1=72.7 Mean2=67.17Mean1=72.7 Mean2=67.17
 Variance1=128.46 Variance2=157.787Variance1=128.46 Variance2=157.787
 Df = n1+n2-2=20Df = n1+n2-2=20
 t = 1.074t = 1.074
 The tabulated t, 2 sides, for alpha 0.01 is 2.845The tabulated t, 2 sides, for alpha 0.01 is 2.845
 Then accept Ho and conclude that there is noThen accept Ho and conclude that there is no
significant difference between the 2 means. Thissignificant difference between the 2 means. This
difference may be due to chance.difference may be due to chance.
 P>0.01P>0.01

10. 1010
3.One sample in two occasions3.One sample in two occasions
 Mention steps of testing hypothesis.Mention steps of testing hypothesis.
 The df here = n – 1.The df here = n – 1.
n
sd
d
t
−
=
1
)( 2
2
−
−
=
∑
∑
n
n
d
d
sd

11. 1111
Example: Blood pressure of 8Example: Blood pressure of 8
patients, before & after treatmentpatients, before & after treatment
BP beforeBP before BP afterBP after dd dd22
180180 140140 4040 16001600
200200 145145 5555 30253025
230230 150150 8080 64006400
240240 155155 8585 72257225
170170 120120 5050 25002500
190190 130130 6060 36003600
200200 140140 6060 36003600
165165 130130 3535 12251225
Mean d=465/8=58.125Mean d=465/8=58.125 ∑∑d=465d=465 ∑∑dd22
=29175=29175

12. 1212
Results and conclusionResults and conclusion
 t=9.387t=9.387
 Tabulated t (df7), with level of significanceTabulated t (df7), with level of significance
0.05, two tails, = 2.360.05, two tails, = 2.36
 We reject Ho and conclude that there isWe reject Ho and conclude that there is
significant difference between BP readingssignificant difference between BP readings
before and after treatment.before and after treatment.
 P<0.05.P<0.05.